Calculateur de taux de variation moyen
Le calculateur de taux de variation moyen est là pour vous aider à comprendre le concept simple qui se cache derrière un nom long et un peu confus. Mais alors, qu'est-ce que le taux de variation ? D'une manière générale, il montre la relation entre deux facteurs. Vous trouverez ci-dessous une définition plus précise du taux de variation moyen. Nous allons également démontrer et expliquer la formule du taux de variation moyen à l'aide de quelques exemples.
Vous êtes plutôt du genre à regarder une vidéo que de lire ? Apprenez tout ce dont vous avez besoin en 90 secondes grâce à cette vidéo que nous avons réalisée pour vous :
Définition du taux de variation moyen : qu'est-ce que le taux de variation ?
Tout bouge. Le changement est inévitable. En commençant par l'accélération de votre vélo ou de votre voiture, en passant par la croissance de la population, du flux sanguin dans vos veines à la symbiose de vos cellules, le taux de variation nous permet d'établir la valeur associée à ces changements.
Le taux de variation moyen est un taux qui décrit comment un nombre change, en moyenne, par rapport à un autre. Si vous avez une fonction, c'est le coefficient directeur de la droite tracée entre deux points. Vous pouvez utiliser le taux de variation moyen pour n'importe quelle fonction, et pas seulement pour les fonctions linéaires.
🙋 Pour en savoir plus sur le coefficient directeur, consultez le calculateur de coefficient directeur.
Formule du taux de variation moyen
Dans l'image suivante, nous avons marqué deux points pour vous aider à mieux comprendre comment trouver le taux de variation moyen.
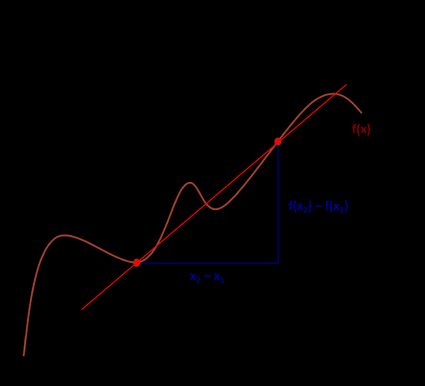
La formule du taux de variation moyen est la suivante :
A = [f(x₂) - f(x₁)] / [x₂ - x₁]
où :
- (x₁, f(x₁)) – coordonnées du premier point
- (x₂, f(x₂)) – coordonnées du deuxième point
Si c'est positif, cela signifie que l'une des coordonnées augmente à mesure que l'autre augmente également. Par exemple, plus vous faites du vélo, plus vous brûlez de calories.
Si elle est égale à zéro, cela signifie que l'une des coordonnées change mais pas l'autre. Un bon exemple serait de ne pas étudier pour vos examens. Lorsque le temps commence à s'écouler, la quantité de choses à apprendre ne change pas.
Le taux de variation moyen est négatif lorsqu'une coordonnée augmente tandis que l'autre diminue. Supposons que vous partiez en vacances. Plus vous passez de temps à voyager, plus vous vous rapprochez de votre destination.
💡 Vous pouvez apprendre d'autres façons de décrire la différence entre deux points dans le calculateur de dénivelé sur la longueur 🇺🇸.
Exemple 1 : comment trouver le taux de variation moyen ?
Calculons le taux de variation moyen de la distance (vitesse moyenne) d'un train allant de Paris à Rome (1 420,6 km). Sur le graphique suivant, vous pouvez voir l'évolution de la distance au fil du temps :
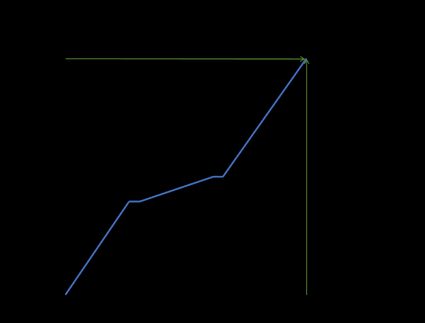
Comme vous le voyez, la vitesse n'est pas constante. Le train s'est arrêté deux fois et, entre les deux arrêts, il a ralenti de façon significative. Mais pour calculer la vitesse moyenne, les seules variables qui comptent sont la variation de la distance et la variation du temps. Ainsi, si les coordonnées du premier point sont (0, 0), que les coordonnées du second point sont la distance entre deux villes et que le temps de parcours est (1420,6, 12,5), alors :
A = (1 420,6 - 0) / (12,5 - 0) = 113,648 [km/h]
En moyenne, le train roulait à 113,648 km par heure. Prenons maintenant un exemple plus mathématique.
Exemple 2 : comment trouver le taux de variation moyen ?
Voici une fonction :
f(x) = x² + 5x - 7
Trouvez le taux de variation moyen sur l'intervalle [-4, 6].
-
Trouvez les valeurs de votre fonction pour les deux points :
f(x₁) = f(-4) = (-4)² + 5 × (-4) - 7 = -11
f(x₂) = f(6) = 6² + 5 × 6 - 7 = 59
-
Utilisez l'équation du taux de variation moyen :
A = [f(x₂) - f(x₁)] / [x₂ - x₁] = [f(6) - f(-4)] / [6 - (-4)] = [59 - (-11)] / [6 - (-4)] = 70 / 10 = 7
Si vous avez aimé le calculateur de taux de variation moyen, n'hésitez pas à consulter nos autres outils comme ce calculateur de distance, qui vous permet de trouver la distance entre des points ou des droites.
Le taux de variation moyen est-il identique au coefficient directeur ?
Pas précisément. Le taux de variation moyen reflète la façon dont une fonction varie en moyenne entre deux points. À l'inverse, nous définissons le coefficient directeur d'une fonction comme la pente de la droite tangente à la courbe en un point précis. Dans une fonction linéaire, chaque point varie de manière identique, de sorte que le taux de variation moyen et le coefficient directeur sont égaux.
Comment trouver le taux de variation moyen d'une fonction ?
Pour trouver le taux de variation moyen d'une fonction, procédez comme suit :
-
Prenez les coordonnées (x, y) du point de départ. Nous les appellerons (x₀, y₀).
-
Prenez les coordonnées (x, y) du point d'extrémité. Elles seront (x₁, y₁).
-
Remplacez les deux dans la formule du taux de variation moyen (A) :
A = (y₁ - y₀)/(x₁ - x₀)
Quel est le taux de variation moyen de y = 2x ?
Le taux de variation moyen de y = 2x est de 2. Comme il s'agit d'une fonction linéaire, le taux de variation moyen est simplement le coefficient directeur de la fonction. Dans ce cas, pour chaque changement de la coordonnée x, la coordonnée y doublera.
La vitesse est-elle un exemple de taux de variation moyen ?
Si la vitesse est constante, oui. La vitesse reflète la façon dont la position change instantanément par rapport au temps. Ainsi, si un objet bougeait à une vitesse constante, le taux de variation moyen de sa position nous indiquerait à quelle vitesse il se déplace.