Calculateur de code couleur des résistances

Avec ce calculateur de code couleur des résistances, vous trouverez rapidement et facilement la résistance de votre résistor ou résistance. Choisissez le nombre d'anneaux de votre résistance (4, 5 ou 6), sélectionnez les couleurs, et en un clin d'œil, vous obtiendrez la résistance, ainsi que la tolérance, la plage de tolérance et la valeur du coefficient de température. La dernière variable n'apparaîtra que si vous avez choisi le code couleur des résistances à 6 anneaux.

Si vous voulez apprendre à lire le code couleur des résistances, faites défiler la page vers le bas, et vous trouverez leurs formules et de nombreuses explications. Nous vous montrerons également à quoi ressemble le code couleur d'une résistance de 10 kΩ ainsi que pleins d'autres exemples.

Les anneaux de couleur sont un moyen simple et bon marché d'indiquer la valeur d'un composant électronique. Les codes alphanumériques imprimés seraient trop petits pour être lus sur les résistances les plus minuscules, ainsi un code couleur a été développé au début des années 1920.

La première question qui se pose généralement est de savoir par quelle extrémité il faut commencer à lire le code couleur d'une résistance.

Heureusement, il existe quelques indices visuels !

• La plupart du temps, les anneaux ne sont pas espacés de manière régulière : il y a un espace, et les anneaux sont en quelque sorte groupés. L'anneau le plus large se trouve avant l'anneau de tolérance. Placez le groupe le plus important à gauche et lisez les résistances de gauche à droite.

• Très souvent, la tolérance de la résistance est égale à 5 ou 10 %. Ces valeurs sont indiquées par des couleurs métalliques : or et argent, respectivement. Cependant, le code couleur des résistances ne commence jamais à partir de ces couleurs. Ainsi, si vous avez une couleur métallique sur votre résistance, il s'agit certainement de la valeur de tolérance, et elle doit donc être placée sur le côté droit. Encore une fois, lisez la résistance de gauche à droite.

• En général, le premier anneau sera le plus proche de l'extrémité (mais pas toujours, utilisez alors d'autres indices pour le savoir).

Si aucun des indices ci-dessus ne semble résoudre votre problème, vous pouvez toujours utiliser un multimètre pour différencier deux résistances possibles. Il suffit ensuite de lire les indications sur l'écran.

Bon, passons aux choses sérieuses : comment lire le code couleur d'une résistance ?

La valeur de la résistance est indiquée par des couleurs. Chaque couleur correspond à un nombre différent :

C'est le code couleur qui fonctionne pour les 2 ou 3 premiers anneaux, se situant le plus à gauche.

Ensuite, nous avons l'anneau appelé multiplicateur ; la signification de la couleur est différente :

Ici, la couleur représente la puissance de 10, par laquelle le nombre créé à partir des anneaux précédents doit être multiplié. Vous pouvez exprimer les multiplicateurs avec des préfixes tels que kilo, méga ou giga ($\mathrm{kΩ}$, $\mathrm{MΩ}$, $\mathrm{GΩ}$), mais la notation scientifique est également utilisée : par exemple, $10^9\ \mathrm{Ω}$ (gigaohm).

Enfin, le dernier anneau, que l'on retrouve dans tous les types de résistances (anneaux 4, 5 et 6) est un anneau de tolérance. La tolérance est exprimée en pourcentages, et la variation dans la résistance des composants est principalement de nature statistique (et suit une loi normale) :

Voilà donc tout ce que vous devez savoir sur la signification du code couleur des résistances à 4 et 5 anneaux. Pour les résistances à 6 anneaux, il y a un anneau supplémentaire qui indique le coefficient de température. Apprenez-en davantage dans un paragraphe un peu plus bas dédié aux résistances à 6 anneaux. Faites défiler la page et découvrez les formules, en fonction du type de votre résistance !

Nous nous sommes efforcés de rendre le calculateur de code couleur des résistances aussi simple et intuitif que possible, mais si vous rencontrez des difficultés, jetez un coup d'œil à l'exemple ci-dessous !

1. Choisissez le nombre d'anneaux sur votre résistance. Il y a trois options : 4, 5 ou 6 anneaux. Supposons que vous ayez une résistance avec 5 anneaux.

2. Choisissez les couleurs des anneaux. Si vous ne savez pas quel est le premier et le dernier anneau, regardez les images intégrées au calculateur. En général, il y a un espace avant l'anneau de tolérance, c'est ainsi que vous pouvez reconnaître le début et la fin. Dans notre exemple, disons que vous avez les couleurs suivantes : marron, rouge, violet, noir et rouge.

3. Le calculateur dessine les anneaux colorés. Comparez-les avec votre résistance. Sont-ils dans le même ordre ?

4. Lorsque vous avez fini d'entrer tous les anneaux, le calculateur de code couleur des résistances vous indique la résistance, avec la tolérance et les valeurs maximale et minimale de cette tolérance. Dans notre exemple, la résistance doit être égale à $127\ \mathrm{Ω}$. De plus, si vous avez saisi un code couleur des résistances à 6 anneaux, la signification du 6ᵉ anneau sera également affichée : le coefficient de température, en $\small\mathrm{ppm/\degree C}$ (aussi noté : $\small\mathrm{ppm\cdot\!\degree C^{-1}}$).

Nous disposons par ailleurs d'autres outils similaires, comme le calculateur de résistance de câble électrique ou le calculateur de résistance pour LED 🇺🇸, afin de déterminer la résistance que vous devez utiliser lorsque vous créez un circuit électronique avec des LED. Vous pouvez aussi consulter notre calculateur de pont de Wheatstone 🇺🇸.

La formule pour le code couleur des résistances à 4 anneaux peut être écrite comme suit :

Mais qu'est-ce que cela signifie et comment le lire ? Regardons l'exemple suivant :

1. Supposons que vous ayez une résistance avec 4 anneaux de couleur. Les couleurs sont : vert, rouge, rouge et or.

2. Prenez les deux premières couleurs : vert et rouge. Les chiffres correspondants sont 5 et 2. Regroupez-les et vous obtiendrez le nombre 52. Formellement, cela s'écrit ainsi :

3. Prenez le troisième anneau : rouge. Cette fois, la signification est différente, car il s'agit de l'anneau multiplicateur, et le facteur correspondant est $100\ \mathrm{Ω}$. Multipliez le résultat précédent par cette valeur.

Et c'est tout ! Voilà la valeur de votre résistance. Maintenant, passons au dernier anneau :

4. Il s'agit de l'anneau de tolérance. Dans notre cas, l'anneau est en or, donc la tolérance est égale à $5\ \%$. Cela signifie que la valeur de votre résistance n'est pas exactement de $5,\!2\ \mathrm{kΩ}$, mais de $5,\!2\ \mathrm{kΩ} \pm 5\ \%$. La valeur peut donc se situer n'importe où dans l'intervalle $\langle R_{\mathrm{min}}, R_\mathrm{max}\rangle$ :

   Valeur minimale :

   $R_{\mathrm{min}} = R - (\mathrm{anneau}_4 \times R)$

   Ainsi, nous obtenons :

Valeur maximale :

$R_{\mathrm{max}} = R +(\mathrm{anneau}_4 \times R)$

Dans notre exemple, cela nous donne :

Et voilà ! Ce n'était pas si difficile, n'est-ce pas ? Vérifiez le résultat avec notre calculateur de code couleur des résistances.

La différence entre les résistances à 4 et 5 anneaux réside dans les chiffres significatifs. Le nombre de chiffres significatifs est de 2 et 3, respectivement. Nous pouvons donc écrire la formule pour le code couleur des résistances à 5 anneaux comme suit :

Continuons avec l'exemple précédent. Après deux anneaux significatifs, le vert et le rouge, plaçons le bleu :

1. Pour vert, rouge et bleu, les chiffres correspondants sont 5, 2 et 6. C'est notre nombre : $526$. Écrivez-le formellement comme suit :

2. Le quatrième anneau rouge est à nouveau notre anneau multiplicateur, avec le facteur correspondant de $100 Ω$. Multipliez le résultat obtenu par cette valeur :

Ainsi :

3. Enfin, l'anneau de tolérance de couleur or signifie que la tolérance est de $5\ \%$. La résistance peut se situer n'importe où dans la plage $\langle R_{\mathrm{min}}, R_\mathrm{max}\rangle$ :

   Valeur minimale :

   $R_{\mathrm{min}} = R - (\mathrm{anneau}_5 \times R)$

   Et donc, cela nous donne :

Valeur maximale :

$R_{\mathrm{max}} = R + (\mathrm{anneau}_5 \times R)$

Dans notre cas, nous avons :

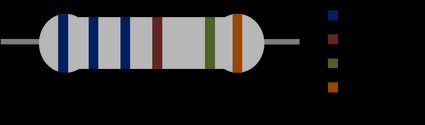
Le code couleur d'une résistance à 6 anneaux est presque le même que celui d'une résistance à 5 anneaux, mais il comprend en plus un anneau pour le coefficient de température à la dernière position. Ce coefficient de température de résistance (angl. temperature coefficient of resistance, TCR) définit la variation de la résistance en fonction de la température ambiante, et s'exprime en $\small\mathrm{ppm/\degree C}$ (aussi noté : $\small\mathrm{ppm\cdot\!\degree C^{-1}}$).

Par exemple, supposons que nous ayons une résistance dont le TCR est égal à $50\ \mathrm{ppm\cdot\!\degree C^{-1}}$. Dans ce cas, cela signifie que la résistance ne variera pas de plus de $0,\!000\,05\ \mathrm{Ω}$ par ohm et par degré Celsius de changement de température. Cependant, cette variation est limitée à la plage de température de référence indiquée dans la notice de l'élément. Maintenant que nous connaissons le TCR et que nous savons que la valeur initiale de la résistance à température ambiante $T_0 = 25\ \mathrm{\degree C}$ est égale à, par exemple, $R_0 = 50\ \mathrm{Ω}$, nous pouvons calculer la résistance $R$ après avoir chauffé ou refroidi l'élément à une autre température, par exemple, $T = 50\ \mathrm{\degree C}$ :

Pour ces calculs, nous pouvons également utiliser le kelvin au lieu du degré Celsius, car c'est la différence entre les températures qui importe, et non la valeur absolue de la température.

Un concept similaire au TCR est le coefficient de dilatation thermique (CTE) : ici, ce n'est pas la résistance, mais la longueur ou le volume de l'élément qui change avec la température.

Attention ! Parfois, le sixième anneau ne désigne pas le coefficient thermique, mais la fiabilité de la résistance, cependant ce sont des cas sporadiques.

Les couleurs du dernier anneau sont codées comme suit :

Il existe de nombreuses options, en fonction de la tolérance et du nombre d'anneaux.

• Code de couleur des résistances à 4 anneaux pour une résistance de 10  kΩ

Les trois premiers groupes sont toujours les mêmes :

1. Le premier anneau est marron, et correspond à 1.
2. Le deuxième anneau est noir, ce qui signifie 0.
3. Le troisième anneau : multiplicateur × $1\ \mathrm{kΩ}$ est orange.
4. Le quatrième anneau dépend de la valeur de la tolérance : ainsi n'importe quelle couleur est possible pour l'anneau de tolérance.

Vérifions rapidement les calculs :

Nickel !

• Code couleur des résistances 5 et 6 anneaux pour une résistance de 10 kΩ

Les quatre premiers anneaux sont toujours fixes :

1. Le premier anneau est marron, et correspond à 1.
2. Le deuxième anneau est noir, ce qui signifie 0.
3. Le troisième anneau est noir, ce qui signifie, encore 0.
4. Le quatrième anneau est un multiplicateur × $100\ \mathrm{Ω}$ qui est rouge.
5. Le cinquième (et le sixième) anneau peut être différent, car il s'agit des valeurs de tolérance et de coefficient thermique.

Vérifions à nouveau :

Cela fonctionne. Super !

Voici comment lire les résistances à 4 ou 5 anneaux codées par couleur :

1. Trouvez le sens de lecture : il doit y avoir un espace plus important entre les deux derniers anneaux.
2. Observez les deux premiers (4 anneaux) ou trois anneaux (5 anneaux) et attribuez leur couleur aux chiffres.
3. Vérifiez la couleur de l'anneau multiplicateur, qui indique la valeur par laquelle les chiffres sont multipliés.
4. Attribuez la couleur de l'anneau de tolérance à la valeur.

Commencez à lire là où les anneaux colorés sont regroupés plus étroitement. Tenez la résistance avec ces anneaux groupés vers la gauche. Vous devriez remarquer un espace entre les anneaux et le dernier anneau (ou les deux derniers dans le cas d'une résistance à 6 anneaux). Les résistances doivent toujours être lues de gauche à droite.

1 kΩ ± 5 %, si l'on suppose que son code couleur est marron-noir-noir-marron-or. Pour le savoir :

1. Attribuez des numéros aux couleurs des trois premiers anneaux : cela fait 100.
2. Trouvez le multiplicateur pour le quatrième anneau de couleur marron : 10.
3. Multipliez 100 par 10.
4. L'or indique une marge d'erreur de 5 % : la résistance sera donc comprise entre 950 Ω et 1 050 Ω.

Le code couleur est rouge-rouge-marron-or. Le premier chiffre significatif est 2, et la valeur 2 correspond à la couleur rouge. Le deuxième chiffre significatif est également 2, ce qui nous donne également rouge. Le multiplicateur est 10 (22 × 10 = 220 Ω), le troisième anneau sera donc marron. Nous pouvons accepter une résistance avec une marge d'erreur de 5 %, le dernier anneau est donc de couleur or.

L'anneau de fiabilité détermine le taux d'échec (%) pour 1 000 heures de travail. Vous pouvez rencontrer cet anneau supplémentaire sur des résistances spécifiques utilisées par l'armée. Toutefois, cet anneau est rarement utilisé dans l'électronique grand public.