Calculateur d'écart type de la moyenne de l'échantillon

Le calcul de l'écart type de la moyenne de l'échantillon est un excellent moyen de comprendre l'influence de la taille de l'échantillon sur l'erreur de nos estimations.

Lorsque l'écart type de la moyenne est multiplié par une valeur critique, comme le score Z ou score T, nous obtenons une marge d'erreur qui permet d'établir un intervalle de confiance de notre prédiction. Par conséquent, le calcul de l'écart type de la moyenne de l'échantillon indique où pourrait se situer la moyenne de la population.

Tout d'abord, il est important de préciser que ce terme est connu sous différentes appellations telles que :

• l'écart type de la moyenne ;
• l'écart type de la moyenne de l'échantillon ; et
• l'écart type de la distribution de la moyenne de l'échantillon ; et
• l'écart type de la distribution d'échantillonnage de la moyenne de l'échantillon.

Il est également essentiel de connaître quelques définitions et concepts.

• Statistique : estimation ponctuelle ou caractéristique numérique d'un échantillon (c'est-à-dire la moyenne de l'échantillon). Elle diffère d'un paramètre, tel que la moyenne de la population.
• Distribution d'échantillonnage : la loi de probabilité d'une statistique échantillonnée au hasard. En d'autres termes, il s'agit de la distribution de toutes les valeurs possibles qu'une statistique pourrait prendre en utilisant la même taille d'échantillon.
• Distribution d'échantillonnage de la moyenne d'un échantillon : il s'agit d'une extension du concept précédent. Si vous disposez d'une population, que vous prenez une infinité d'échantillons de taille n et que vous représentez leurs moyennes dans un histogramme, vous obtenez une loi de probabilité. Cette loi de probabilité est ce que nous appelons la distribution d'échantillonnage de la moyenne, et comme toute autre distribution, elle a sa propre moyenne et son propre écart type.

Le diagramme suivant montre comment générer une distribution de la moyenne d'un échantillon. En réalité, nous n'utilisons pas seulement six échantillons, mais un nombre presque infini (c'est-à-dire 100 000).

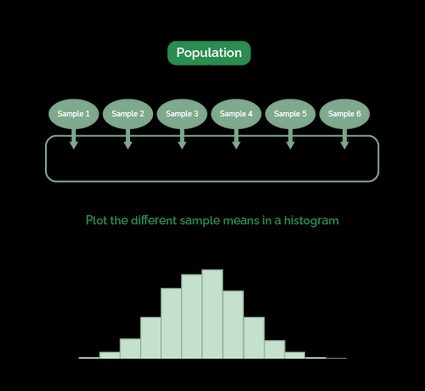
Cela dit, nous pouvons définir l'écart type moyen comme étant l'écart type d'une distribution de moyennes (comme celle illustrée dans le dernier diagramme). En outre, la moyenne de cette distribution d'échantillonnage est égale à la moyenne de la population.

Maintenant que vous connaissez le concept, voyons comment calculer l'écart type de la moyenne d'un échantillon.

La différence entre la distribution de l'échantillon et la distribution d'échantillonnage est la suivante.

• Distribution d'échantillonnage : c'est le terme que nous entendons habituellement. Il désigne la loi de probabilité d'une statistique échantillonnée au hasard. La distribution d'échantillonnage de la moyenne en est un exemple.
• Distribution de l'échantillon : elle représente la distribution des observations au sein d'un seul échantillon. Chaque distribution d'échantillon possède une moyenne, qui contribue à former la distribution d'échantillonnage.

La formule pour trouver l'écart type de la moyenne de l'échantillon est la suivante :

σ_X̄ = σ/√n

où :

• σ_X̄ – écart-type de la moyenne de l'échantillon
• σ – écart-type de la population
• n – taille d'échantillon

Nous avons dit précédemment que si nous connaissons la moyenne de la distribution d'échantillonnage (μ_X̄), nous connaissons également la moyenne de la population (μ), car elles sont égales (μ_X̄ = μ). En pratique, nous ne connaissons jamais μ_X̄, mais nous pouvons l'estimer en utilisant la moyenne de l'échantillon (X̄).

σ_X̄ indique dans quelle mesure X̄ se rapproche de μ. Plus σ_X̄ est petit, plus μ peut être proche de notre estimation. Comme σ est constant, l'augmentation de la taille d'échantillon est le seul moyen de diminuer σ_X̄. Par conséquent, l'augmentation de n est un moyen de réduire l'erreur d'échantillonnage 🇺🇸 de nos estimations.

Nous savons que la moyenne et l'écart type de la taille de la population féminine américaine adulte sont d'environ μ = 161,3 cm et σ = 7,1 cm. Supposons maintenant que vous préleviez au hasard des échantillons de 100 femmes et que vous preniez à chaque fois leur taille moyenne. Quel est l'écart type de la moyenne de l'échantillon ?

Pour connaître la réponse, suivez ces étapes :

1. Saisissez 7,1 dans le champ de l'écart type de la population.
2. Entrez 100 dans le champ taille d'échantillon.
3. Et le tour est joué. La réponse devrait être 0,71. Par conséquent, l'écart type de la distribution de la moyenne pour n = 100 est 0,71.

Vous pouvez vérifier les résultats en utilisant la formule  : $σ_{\bar X} = \frac{σ}{\sqrt{n}} = \frac{7,\!1}{\sqrt{100}} = 0,\!71$