Calculateur de probabilité
Le calculateur de probabilité permet d'analyser les probabilités de deux événements distincts. Par exemple, si la probabilité de A est de 50 %, et pareil pour B, quelles sont les chances que les deux se produisent, qu'un seul se produise, qu'au moins un se produise, ou qu'aucun ne se produise ?
Notre calculateur de probabilité propose six scénarios, plus six autres si vous entrez le nombre de fois où l'événement se produit. Si vous connaissez les formules de probabilité, vous pouvez calculer les probabilités de chaque événement vous-même, mais le calculateur vous fera gagner du temps.
Dans cet article, vous apprendrez :
- comment utiliser le calculateur de probabilités ;
- comment trouver la probabilité d'événements uniques ;
- de nombreux exemples d'utilisation des probabilités, y compris les formules de probabilité conditionnelles ;
- la différence entre la probabilité théorique et la probabilité fréquentielle ; et
- la relation entre les probabilités et les statistiques.
Vous êtes venu ici spécialement pour vérifier vos chances de gagner un pari ou de toucher le jackpot ? Nos calculateur de chances et calculateur de loterie 🇺🇸 sont là pour vous !
Définition de la probabilité : Comment calculer la probabilité d'un événement ?
La définition de base de la probabilité est le rapport entre le nombre de résultats favorables et le nombre total de résultats possibles.
Les probabilités élémentaires sont comprises entre 0 et 1, c'est pourquoi il est également pratique de les exprimer en pourcentage. La probabilité d'un événement élémentaire peut être exprimée comme suit :
- la probabilité de
A:P(A); - la probabilité de
B:P(B); - la probabilité de
+:P(+); - la probabilité de
♥:P(♥); - etc.
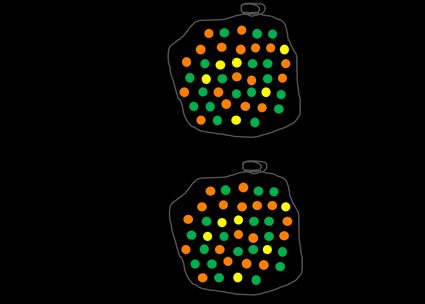
Prenons un exemple avec des boules multicolores. Nous avons un sac rempli de boules orange, vertes et jaunes. Notre événement A consiste à prendre une boule au hasard dans le sac. Nous pouvons définir Ω comme l'ensemble de toutes les boules. La probabilité de l'événement Ω, qui consiste à piocher n'importe quelle boule, est naturellement de 1. En effet, la somme de tous les événements possibles dans un ensemble donné est toujours égale à 1.
Examinons maintenant une question plus difficile : quelle est la probabilité de choisir une boule orange ? Pour répondre à cette question, vous devez trouver le nombre de boules orange et le diviser par le nombre total de boules dans le sac. Vous pouvez faire la même chose pour n'importe quelle couleur. Vous remarquerez que plus il y a de boules d'une couleur particulière, plus la probabilité de la piocher dans le sac est élevée si le processus est totalement aléatoire.
Consultez nos calculateur de probabilités pour 3 événements 🇺🇸 et calculateur de probabilités conditionnelles 🇺🇸 pour déterminer les chances d'événements composés.

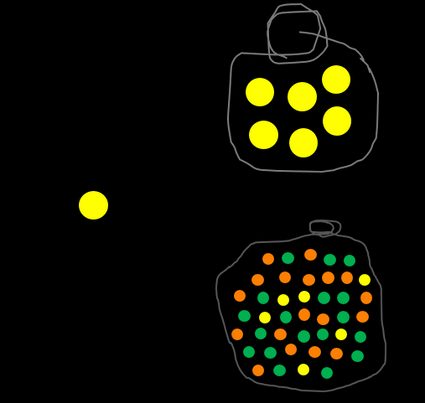
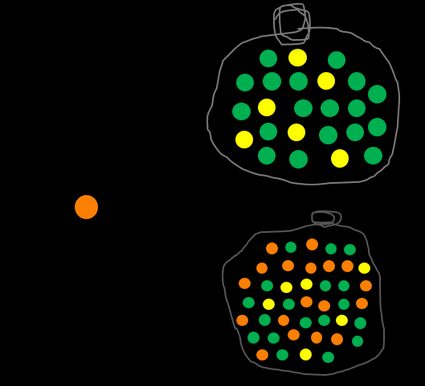
Nous pouvons définir un événement complémentaire, noté Ā ou A', qui signifie non A. Dans notre exemple, la probabilité de ne PAS piocher une boule orange est évaluée comme le nombre de boules non oranges divisé par le nombre total de boules. La somme P(A) + P(Ā) est toujours égale à 1, car il n'y a pas d'autre option, comme une demi-boule ou une boule semi-orange.
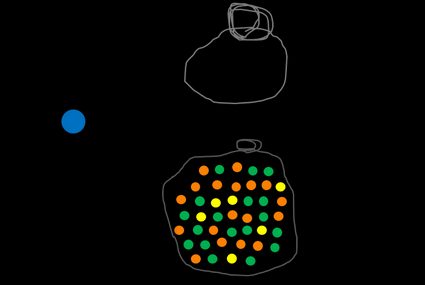
Voyons maintenant la probabilité d'obtenir une boule bleue. Même si vous essayez un million de fois, vous n'en piocherez jamais une, car il n'y en a aucune dans le sac. La probabilité est donc nulle.
Nous utilisons des calculs intuitifs de probabilité au quotidien. Savoir quantifier la probabilité est essentiel pour l'analyse statistique. Cela nous permet de mesurer des concepts complexes comme la « probabilité » d'échec ou de succès. De plus, puisque l'ensemble est composé de données discrètes, la fréquence relative 🇺🇸 de chaque valeur est synonyme de la probabilité de leur apparition. En d'autres termes, si vous lancez un dé 100 fois, la fréquence relative de chaque face sera égale à la probabilité d'obtenir cette face.
Vous cherchez quelque chose de légèrement différent ? Jetez un coup d'œil à notre calculateur de probabilité de post-test 🇺🇸. 🎲
Probabilité conditionnelle
L'une des notions les plus importantes en probabilité est la dépendance des événements. Deux événements sont indépendants si l'occurrence du premier n'affecte pas la probabilité d'occurrence du second. Par exemple, si nous lançons un dé cubique standard parfaitement équilibré, la possibilité d'obtenir un deux ⚁ est égale à 1/6, quelle que soit la valeur obtenue au lancer précédent.
Supposons que vous lanciez deux dés et que vous obteniez un cinq ⚄ au premier lancer. La probabilité d'obtenir un deux ⚁ au deuxième lancer est toujours de 1/6, car les deux événements sont indépendants.
La manière de penser et de calculer la probabilité change si l'un des événements perturbe l'ensemble du système. Cette fois, nous parlons de probabilités conditionnelles.
Supposons que vous disposiez de 10 boules de billard différentes, numérotées de ➀ à ➉. Vous choisissez une boule au hasard : la probabilité d'obtenir la boule sept ➆ est alors précisément de 1/10. Supposons que vous ayez pioché la boule trois ➂ et que vous l'ayez retirée du jeu. Vous vous demandez, une fois de plus, quelle est la probabilité d'obtenir le sept ➆. La probabilité a changé, car il y a une qu'une boule avec le numéro sept ➆ sur neuf possibilités, ce qui signifie que la probabilité est maintenant de 1/9. Autrement dit, on peut formuler le problème ainsi : « Quelle est la probabilité de choisir la boule sept ➆, SACHANT que la boule trois ➂ a déjà été tirée ? »
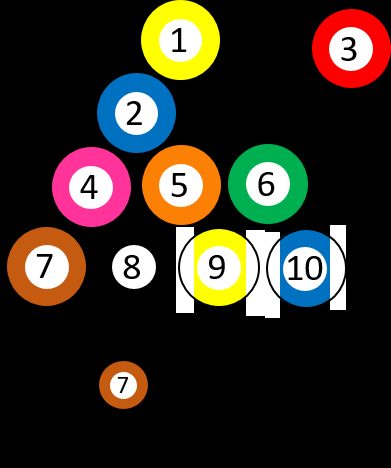
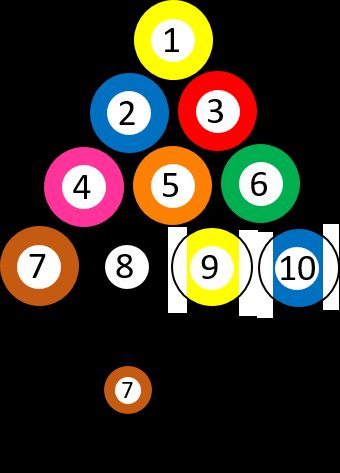
Prenons un autre exemple : imaginez que vous deviez passer un examen de statistiques. Vous savez par vos camarades plus âgés qu'il s'agit d'un examen difficile, et la probabilité de le réussir du premier coup est de 0,5 (18 étudiants sur 36 l'ont réussi l'année dernière). Maintenant, posez-vous la question suivante : « Quelle est la probabilité de réussir SACHANT que j'ai déjà révisé le sujet » 20 personnes ont admis avoir révisé leurs notes au moins une fois avant l'examen, et 16 d'entre elles ont réussi. Cela signifie que la réponse à votre question est de 0,8. Ce résultat indique que cette condition supplémentaire est vraiment importante pour savoir si le fait d'étudier change quelque chose ou non.
Si vous ne comprenez toujours pas le concept de probabilité conditionnelle, essayons avec un autre exemple : vous devez vous rendre en voiture de la ville X à la ville Y. La distance entre les deux villes est d'environ 150 km. Avec un plein, vous pouvez généralement parcourir jusqu'à 400 km. Si vous ne connaissez pas le niveau de carburant, vous pouvez estimer la probabilité d'atteindre votre destination sans faire le plein. Si vous savez que quelqu'un a déjà fait le plein, vous êtes presque sûr d'y arriver, à moins que d'autres problèmes ne vous en empêchent.
Formule de la probabilité conditionnelle
L'expression générale de la probabilité conditionnelle, qui peut être désignée par P(A|B), P(A/B) ou PB(A), peut être calculée comme suit :
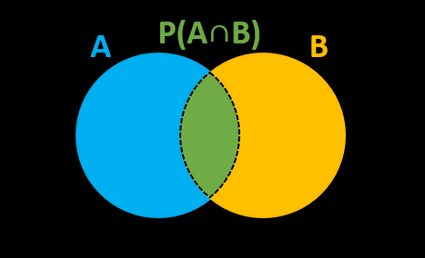
P(A|B) = P(A∩B) / P(B)
où :
P(B) – la probabilité d'un événement B
P(A∩B) – la probabilité conjointe des deux événements
D'autre part, nous pouvons estimer l'intersection de deux événements si nous connaissons l'une des probabilités conditionnelles :
P(A∩B) = P(A|B) × P(B)
ou
P(A∩B) = P(B|A) × P(A)
La probabilité conditionnelle est un concept difficile à comprendre, il est alors plus facile de le visualiser à l'aide de diagrammes en arbre.
Nous demandons aux élèves d'une classe s'ils aiment les mathématiques et la physique. L'événement « M » indique le pourcentage d'élèves qui aiment les mathématiques, et « P » le même pourcentage pour la physique :

Il existe un théorème célèbre qui relie les probabilités conditionnelles de deux événements. Il s'agit du théorème de Bayes, dont la formule est la suivante :
P(A|B) = P(B|A) × P(A) / P(B)
Vous pouvez poser la question suivante : « Quelle est la probabilité de A sachant B si je connais la probabilité de B sachant A ? ». Ce théorème donne parfois des résultats surprenants et peu intuitifs. Les exemples les plus courants sont les tests de médicaments et la détection des maladies, qui ont beaucoup en commun avec le risque relatif de maladie dans la population. Concentrons-nous sur le second. Dans un groupe de 1 000 personnes, 10 d'entre elles sont atteintes d'une maladie rare. Le test de dépistage est fiable à 95 %. Nous voulons donc trouver la probabilité qu'une personne soit malade si le résultat de son test est positif.
Si une personne de ce groupe reçoit un résultat positif au test, notre intuition nous dirait que la probabilité qu'elle soit malade est d'environ 90 %, n'est-ce pas ? Faisons le calcul.
- Nous utiliserons la notation suivante :
S – sain
M – malade
+ – test positif
- – test négatif
2. Réécrivons les informations du texte ci-dessus sous forme de probabilités :
P(S) = 0,99
P(M) = 0,01
P(+|M) = 0,95
P(-|M) = 0,05
P(+|S) = 0,05
P(-|S) = 0,95
3. Calculons la probabilité totale d'un test positif : P(+) = P(+|M) × P(M) + P(+|S) × P(S) = 0,95 × 0,01 + 0,05 × 0,99 = 0,059
4. Utilisons le théorème de Bayes pour trouver la probabilité conditionnelle : P(M|+) = P(+|M) × P(M) / P(+) = 0,95 × 0,01 / 0,059 = 0,161
Hmm… ce n'est pas si élevé que cela, n'est-ce pas ? Il s'avère que ce genre de paradoxe apparaît lorsqu'il y a un déséquilibre significatif entre le nombre de personnes saines et malades, ou en général, entre deux groupes distincts. Si le résultat est positif, il est toujours utile de répéter le test pour établir un diagnostic approprié.
Lois de probabilité et fonction de répartition
Les lois de probabilité peuvent être divisées en deux catégories : discrètes et continues.
-
Une loi de probabilités discrètes décrit la probabilité d'événements distincts et dénombrables. Par exemple, la probabilité binomiale, qui prend en compte la probabilité d'un certain type de succès en plusieurs tentatives, comme jouer à pile ou face. En revanche, dans la loi de Pascal (également connue sous le nom de loi binomial négative), le nombre fixe de succès est donné et l'objectif est d'estimer le nombre total d'essais.
La loi de Poisson est une autre loi de probabilités discrètes et est en fait un cas particulier de la loi binomiale, que vous pouvez calculer avec notre calculateur de la loi de Poisson 🇺🇸. La fonction de masse peut être interprétée comme une autre définition de la loi de probabilité d'une variable discrète. Elle attribue des probabilités à chaque résultat possible de la variable aléatoire, indiquant la probabilité d'observer ce résultat particulier. La loi géométrique 🇺🇸 est un excellent exemple d'utilisation de la fonction de masse.
-
Une loi de probabilités continues contient des informations sur des événements indénombrables. Il est impossible de prédire la probabilité d'un seul événement (comme dans une loi discrète), mais plutôt de trouver l'événement dans un intervalle de variables. La loi normale est l'une des lois continues les plus connues. Elle décrit un ensemble de propriétés au sein d'une population, par exemple la taille des adultes ou la répartition du QI. La fonction qui décrit la probabilité d'observer un résultat dans un intervalle de valeurs donné est appelée fonction de densité ou densité de probabilité.
Si vous avez déjà des connaissances sur la théorie des probabilités, vous devriez vous renseigner sur les lois de probabilités mixtes 🇺🇸, qui prennent en compte la combinaison de plusieurs fonctions de probabilité discrètes et continues.
Pour chaque loi de probabilité, nous pouvons construire la fonction de répartition (FDR), aussi appelée fonction de distribution cumulative (FDC). Elle vous indique la probabilité qu'une variable prenne une valeur inférieure ou égale à un nombre donné.
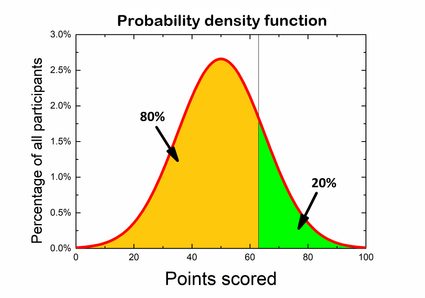
Supposons que vous participiez à un concours de connaissances générales. Le concours comporte 100 questions, et vous gagnez 1 point par bonne réponse, et aucun point par mauvaise réponse. De nombreuses personnes ont déjà terminé, et nous pouvons obtenir une loi de probabilité à partir des résultats. Les règles stipulent que seuls 20 % des meilleurs participants seront récompensés. Vous vous demandez donc quel score vous devriez obtenir pour faire partie des gagnants. Prenez le graphique ci-dessous ; vous pouvez le diviser de façon à ce que 80 % de l'aire sous la courbe se trouve à gauche et 20 % des résultats se trouvent à droite du score souhaité. Ce que vous recherchez en fait, c'est une valeur p unilatérale gauche.
Cependant, il y a aussi une autre manière de trouver la valeur p en utilisant une fonction de répartition. Il suffit de trouver la valeur 80 % sur l'axe des abscisses et le nombre de points correspondant sans avoir besoin de calculer quoi que ce soit !
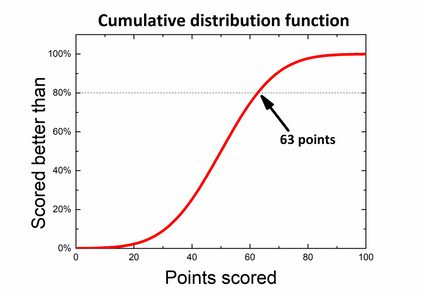
Probabilité théorique et probabilité fréquentielle
Presque tous les exemples décrits ci-dessus prennent en compte la probabilité théorique. Une question se pose donc : quelle est la différence entre la probabilité théorique et la probabilité fréquentielle (également connue sous le nom de probabilité expérimentale) ? La définition formelle de la probabilité théorique est le rapport entre le nombre de résultats favorables et le nombre total de résultats possibles. Elle s'appuie sur les informations données, sur un raisonnement logique, et nous dit ce que nous devons attendre d'une expérience.
Prenons à nouveau nos sacs des boules colorées. Il y a 42 boules au total et 18 sont orange. Le jeu consiste à prendre une boule au hasard dans le sac et à la remettre, de sorte qu'il y a toujours 42 boules à l'intérieur. En appliquant la définition des probabilités, nous pouvons rapidement estimer la probabilité d'obtenir une boule orange à 18/42, ou en simplifiant la fraction, 3/7. Cela signifie que si nous choisissons 14 boules, il devrait y avoir 6 boules orange.
D'autre part, la probabilité expérimentale nous indique précisément ce qui s'est passé lors d'une expérience au lieu de ce qui devrait se passer. Elle est basée sur le rapport entre le nombre de succès et le nombre total d'essais. Restons sur le même exemple : prenons une boule au hasard dans le sac et répétons le processus 13 fois de plus. Supposons que l'on obtient 8 boules orange en 14 essais. Ce résultat signifie que la probabilité fréquentielle est de 8/14 ou 4/7.
Comme vous pouvez le voir, notre dernier résultat diffère du résultat théorique. Cela n'a rien d'étrange, car lorsque nous essayons de répéter ce jeu encore et encore, parfois, nous obtiendrons plus, parfois, nous obtiendrons moins, et parfois, nous obtiendrons exactement le nombre prédit théoriquement. Si nous additionnons tous les résultats, nous devrions remarquer que la probabilité globale se rapproche de plus en plus de la probabilité théorique. Si ce n'est pas le cas, le choix d'une boule n'est pas entièrement aléatoire. Par exemple, si les boules de différentes couleurs ont des tailles inégales, on pourrait les distinguer au toucher.
Probabilités et statistiques
Les probabilités et les statistiques sont deux branches des mathématiques qui s'intéressent à la fréquence d'occurrence d'événements. Cependant, il est important de comprendre les différences entre ces deux disciplines.
-
Les probabilités sont un domaine théorique qui étudie les conséquences des définitions et des théorèmes mathématiques. Les statistiques, quant à elles, sont un domaine appliqué qui utilise les mathématiques pour analyser des données du monde réel.
-
Les probabilités prédisent la possibilité qu'un événement se produise, en se basant sur des informations connues, tandis que les statistiques consistent essentiellement à tirer des conclusions sur la probabilité d'occurrence d'un événement, en se basant sur les observations passées.
-
Pour illustrer ces différences, imaginez un probabiliste qui joue à un jeu de cartes. Le jeu consiste à choisir une carte au hasard dans un jeu complet, sachant que seules les piques gagnent avec un rapport de chances prédéfini. En supposant que le jeu soit complet et que le choix est entièrement aléatoire et équitable, il en déduit que la probabilité est égale à
¼et peut faire un pari. -
Un statisticien, quant à lui, observerait le jeu pendant un certain temps pour vérifier si les règles sont respectées et le jeu, équitable. Après avoir vérifié (avec une approximation acceptable) que le jeu vaut la peine d'être joué, il demandera au probabiliste ce qu'il doit faire pour gagner le plus possible.
Statistiques au sein d'un grand groupe de personnes : échantillonnage probabiliste
Vous avez probablement vu des sondages d'opinion électoraux, et vous vous êtes peut-être demandé·e comment ils peuvent être si précis, même si le nombre de personnes interrogées est bien inférieur à la population totale. C'est là qu'intervient l'échantillonnage probabiliste.
L'idée de base de l'échantillonnage est de choisir des personnes au hasard, avec une probabilité définie à l'avance. Il existe de nombreuses méthodes d'échantillonnage, chacune avec ses propres avantages et inconvénients.
- L'échantillonnage aléatoire simple
- L'échantillonnage aléatoire en grappes
- L'échantillonnage systématique
- L'échantillonnage probabiliste proportionnel à la taille
- L'échantillonnage aléatoire stratifié
- L'échantillonnage minimax
- L'échantillonnage accidentel
- L'échantillonnage par quotas
- L'échantillonnage volontaire
- L'échantillonnage par panel
- L'échantillonnage en boule de neige
- L'échantillonnage par interception linéaire
- L'échantillonnage théorique
Les principaux avantages de l'échantillonnage probabiliste sont le gain de temps et la rentabilité, puisqu'il suffit d'interroger un nombre limité de personnes. La simplicité de cette procédure ne requiert aucune expertise et peut être réalisée sans préparation approfondie.
Application pratique de la théorie des probabilités
Comme vous l'avez peut-être déjà compris, la théorie des probabilités s'applique à de nombreux domaines. La plupart d'entre eux sont des jeux avec un facteur aléatoire élevé, comme le lancer de dés ou le choix d'une boule de couleur parmi 10 couleurs différentes, ou encore de nombreux jeux de cartes. Les loteries et les jeux d'argent sont des types de jeux qui font largement appel au concept de probabilité et généralement au manque de connaissances à ce sujet. Bien sûr, quelqu'un gagne de temps en temps, mais la probabilité que cette personne soit vous est extrêmement faible.
La théorie des probabilités est également utilisée dans de nombreux types de problèmes. En particulier lorsqu'il s'agit d'investissements, il est utile de prendre en compte le risque pour choisir l'option la plus appropriée.
Notre calculateur de Noël blanc 🇺🇸 utilise des données historiques et des connaissances en matière de probabilités pour prédire s'il va neiger chez vous pendant la période de Noël.
Comment calculer la probabilité de A et B ?
Si A et B sont des événements indépendants, vous pouvez multiplier leurs probabilités pour obtenir la probabilité que A et B se produisent. Par exemple, si la probabilité de A est de 20 % (0,2) et la probabilité de B est de 30 % (0,3), la probabilité que les deux se produisent est de 0,2 × 0,3 = 0,06 = 6 %.
Comment calculer une probabilité conditionnelle ?
Pour calculer la probabilité conditionnelle de A sachant B :
- Déterminez la probabilité de B, c'est-à-dire P(B).
- Déterminez la probabilité de A et B, c'est-à-dire P(A∩B).
- Divisez le résultat de l'étape 2 par celui de l'étape 1.
- Le tour est joué ! La formule se lit comme suit : P(A|B) = P(A∩B) / P(B).
Quelle est la probabilité d'obtenir 6 deux fois ?
Si vous utilisez des dés équilibrés, la probabilité d'obtenir 6 deux fois sera de 1/6 × 1/6 = 1/36 = 0,027 = 2,7 %. Cela signifie qu'il faut 36 lancers de dés pour espérer obtenir au moins une fois deux six, bien qu'il n'y ait aucune garantie en matière de probabilité.
Comment convertir la probabilité en pourcentage ?
Convertissez la probabilité en un nombre décimal, puis multipliez par 100. Par exemple, si la probabilité est de 1 sur 9, cela donne 1/9 = 0,111 1 sous forme décimale. Multipliez ensuite par 100 pour obtenir 11,11 %.
Comment utiliser le calculateur de probabilité ?
Pour utiliser efficacement notre calculateur, suivez ces étapes :
1. Définissez le problème que vous souhaitez résoudre.
Votre problème doit pouvoir se diviser en deux événements indépendants.
2. Trouvez la probabilité de chaque événement.
Maintenant que vous savez comment estimer la probabilité d'un seul événement, il vous suffit de faire la même chose et d'obtenir toutes les valeurs nécessaires.
3. Saisissez le pourcentage de probabilité de chaque événement dans les champs correspondants.
Une fois ces valeurs saisies, le calculateur de probabilité affichera immédiatement la probabilité exacte de 6 scénarios différents :
Vous pouvez également choisir d'afficher tous les scénarios ci-dessus. En outre, le calculateur peut aussi afficher la probabilité de six autres scénarios, pour un nombre d'essais donné :
Vous pouvez modifier le nombre d'essais et n'importe quel autre champ du calculateur, et les autres champs s'ajusteront automatiquement. Cette fonctionnalité permet de gagner beaucoup de temps si vous voulez savoir, par exemple, quelle doit être la probabilité de l'événement B pour que la probabilité que les deux événements se produisent soit de 50 %.
Si l'ensemble des choix possibles est extrêmement vaste et que seuls quelques résultats sont probants, la probabilité résultante est minuscule, par exemple,
P(A) = 0,000 1. Il est alors pratique d'utiliser la notation scientifique pour éviter de confondre les zéros.