Calcolatore di Tensione

Questo calcolatore di tensione ti insegnerà a trovare la tensione in una corda o un filo utilizzato per sollevare un oggetto. In questo articolo potrai anche imparare a trovare la tensione delle corde utilizzate per tirare un oggetto su una superficie senza attrito. In questo calcolatore di tensione di corde vedrai anche una serie di diagrammi con esempi di oggetti sospesi liberamente per capire meglio come calcolare le forze di tensione. Se vuoi saperne di più sulla tensione e sulla formula della tensione, continua a leggere!

Immagina di raccogliere una palla da basket da terra. Sentiresti il peso della palla nelle tue mani a causa della forza di gravità che agisce sulla massa della palla. Ora immagina di legare una corda intorno alla palla, che poi userai per sollevarla di nuovo. Sentirai ancora il peso della palla attraverso la corda. In questa situazione, la corda è in tensione. La forza di tensione è ciò che impedisce alla corda di rompersi. Tagliando la corda, la forza di tensione viene rilasciata e la palla cade liberamente.

La tensione è una forza assiale che passa attraverso un oggetto che tira, come una corda, un filo o una catena. Possiamo osservare la tensione anche in altri materiali, come aste e barre, quando sono sottoposti a carichi esterni di trazione. I materiali con un elevato sforzo di trazione sono i migliori per questo compito perché non si rompono facilmente quando sono sottoposti alla trazione. Per saperne di più sulla trazione, puoi consultare il nostro calcolatore di sforzo e deformazione, che parla di elasticità.

La trazione è anche un ottimo esempio del terzo principio della dinamica di Newton. Esso afferma che quando un corpo esercita una forza su un secondo corpo, quest'ultimo esercita una forza uguale in direzione opposta sul primo. La tensione è una forza reattiva che contrasta una forza di trazione esterna.

Per calcolare la tensione che agisce su una corda, dobbiamo prima comprendere il secondo principio della dinamica di Newton. Questo principio afferma che la somma delle forze che agiscono su un oggetto di massa costante è uguale alla massa di quell'oggetto moltiplicata per la sua accelerazione. Possiamo anche esprimere questa affermazione con la seguente equazione:

ΣF = m × a

dove:

• Σ (sigma) — Somma delle forze F;
• m — Massa dell'oggetto; e
• a — Accelerazione.

Per un oggetto sospeso a una corda, possiamo usare l'accelerazione dovuta alla gravità 🇺🇸, g. L'accelerazione gravitazionale ci dà il valore del suo peso in termini di forza, ad esempio in Newton o chilogrammi-forza (kgf). Se l'oggetto si muove con un'accelerazione diversa, dovremmo utilizzare la sua accelerazione effettiva per il calcolo. Tuttavia, questo calcolatore di tensione determina le forze di tensione solo in caso di equilibrio statico.

Ciò significa che questo strumento considera solo oggetti a riposo in un determinato sistema. In questo calcolatore di tensione, inoltre, supponiamo che le corde siano prive di massa e che, quindi, non contribuiscano alle forze di tensione. Supponiamo inoltre che le masse o gli oggetti si trovino nel vuoto e non subiscano attrito o resistenza dell'aria verso l'ambiente circostante.

Nell'illustrazione sottostante possiamo vedere che la forza, F, necessaria per sollevare l'oggetto è uguale al peso dell'oggetto, W. Questa idea è il concetto fondamentale che sta alla base della nostra formula della tensione. Di seguito è mostrato anche il diagramma di oggetti sospesi liberamente, che mostra le forze di tensione, T, che agiscono sulla corda. Come puoi vedere, le forze di tensione agiscono a coppie e in direzioni opposte:

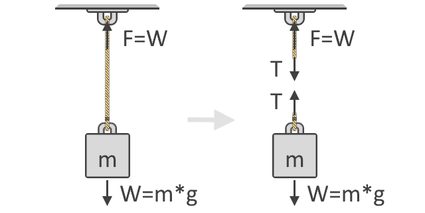
Seguendo il secondo principio della dinamica di Newton, possiamo esprimere la somma delle forze utilizzando il diagramma di un oggetto sospeso liberamente, come mostrato sul lato destro dell'illustrazione qui sopra. Utilizziamo questo tipo di diagrammi per mostrare le diverse direzioni e magnitudini delle forze che agiscono su un corpo. In condizioni di equilibrio, queste forze dovrebbero essere tutte uguali a zero. Considerando tutte le forze verso l'alto come positive e quelle verso il basso come negative, la nostra equazione è:

ΣF↑ = 0 = T + (-W)

T = W

dove il peso, W, diventa negativo poiché è diretto verso il basso. Trasponendo W sull'altro lato dell'equazione, possiamo ora vedere che la forza di tensione della corda è uguale al peso dell'oggetto, come mostrato in precedenza.

Se utilizziamo più corde per sollevare l'oggetto, la forza di tensione totale viene suddivisa tra le corde. La forza di tensione di ogni corda dipende dal suo angolo rispetto alla direzione della forza contraria. Per capire meglio, consideriamo un altro diagramma di un oggetto sospeso da due corde:

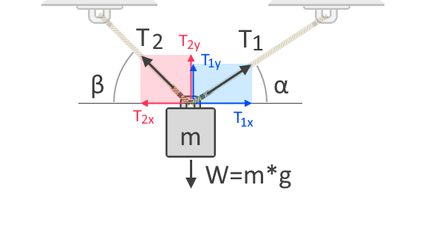
In questo diagramma, possiamo vedere le componenti orizzontali e verticali delle forze di tensione, T₁ e T₂. Le forze sono vettori, il che significa che hanno sempre un modulo e una direzione. Come tutti i vettori, le forze possono essere espresse usando queste componenti, che indicano l'influenza della forza lungo gli assi orizzontale e verticale. T_1x e T_2x sono le componenti orizzontali di T₁ e T₂, rispettivamente. D'altra parte, T_1y e T_2y sono le componenti verticali delle stesse forze, rispettivamente. Poiché la gravità agisce sull'oggetto sull'asse verticale, dobbiamo considerare le componenti verticali delle forze di tensione per la nostra somma di forze come segue:

ΣF↑ = 0 = T_1y + T_2y + (-W)

W = T_1y + T_2y

Poiché conosciamo anche gli angoli delle forze di tensione, possiamo esprimere T_1y e T_2y in termini di T₁ e T₂, rispettivamente, con l'aiuto di funzioni trigonometriche:

T_1y= T₁ × sin(α)

T_2y= T₂ × sin(β)

W = T₁ × sin(α) + T₂ × sin(β)

Possiamo anche dire che, affinché il sistema sia in equilibrio, l'oggetto non deve muoversi orizzontalmente o lungo l'asse x. Pertanto, le componenti orizzontali di T₁ e T₂ devono essere uguali a zero. Inoltre, con l'aiuto della trigonometria, possiamo esprimere T₁ₓ e T₂ₓ in termini di T₁ e T₂, rispettivamente:

T₁ₓ = T₂ₓ

T₁ × cos(α) = T₂ × cos(β)

Se dividiamo entrambi i lati per cos(α), otteniamo un'equazione in cui T₁ è espresso in termini di T₂ e degli angoli:

T₁ = T₂ × cos(β) / cos(α)

Possiamo quindi utilizzare questa equazione per risolvere T₂ sostituendo T₂ × cos(β) / cos(α) come T₁ nella nostra equazione di somma delle forze, come mostrato di seguito:

W = T₁ × sin(α) + T₂ × sin(β)

W = T₂ × [cos(β) / cos(α)] × sin(α) + T₂ × sin(β)

W = T₂ × [cos(β) × sin(α) / cos(α) + sin(β)]

T₂ = W / [cos(β) × sin(α) / cos(α) + sin(β)]

Infine, se moltiplichiamo l'intera equazione per cos(β) / cos(α) come abbiamo ricavato dal valore di T₁ in termini di T₂, e poi semplifichiamo il tutto, otteniamo questa equazione:

T₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]

T₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]

T₁ = W / [cos(α) × sin(β) / cos(β) + sin(α)]

Ora tutto ciò che devi determinare sono gli angoli delle corde rispetto all'asse orizzontale. Se conosci un angolo rispetto all'asse verticale, basta sottrarre questo angolo da 90°. In questo modo otterrai l'angolo rispetto all'asse x. Tuttavia, se ti vengono forniti altri valori di angoli che possono essere maggiori di 90° o addirittura di 180°, potresti dare un'occhiata al nostro calcolatore per angoli orientati per aiutarti a determinare l'angolo di cui hai bisogno. Dopo aver determinato i valori delle variabili nelle formule della forza di tensione, possiamo metterci a calcolarle.

Che l'oggetto venga tirato o regga un altro oggetto appeso a esso, la procedura è la stessa. L'unica differenza è che prima dobbiamo calcolare l'accelerazione dell'intero sistema e sommare tutte le forze lungo l'orizzontale. Se la corda è inclinata rispetto al livello del pavimento, dobbiamo calcolare anche la componente orizzontale della forza di trazione.

Vediamo l'esempio seguente per capire meglio come trovare la forza di trazione di una corda che tira uno o due oggetti. In questo esempio, due oggetti vengono tirati da un'unica forza di trazione. Un'altra corda sta tirando il secondo oggetto, che è attaccato al primo, come mostrato di seguito:

Questa illustrazione mostra che le masse m₁ e m₂ sono pari a 3 kg e 2 kg rispettivamente. La somma di queste due masse dà la massa totale del sistema, 5 kg. Dobbiamo anche determinare la componente orizzontale della forza di trazione, T = 24 N, che si trova ad un angolo θ = 60°. Se usiamo di nuovo le funzioni trigonometriche, possiamo dire che la componente orizzontale della forza di trazione è uguale a 24 N × cos(60°), che è uguale a 12 N. Ora che conosciamo la componente orizzontale della forza di trazione e la massa totale del sistema, possiamo calcolare l'accelerazione, a, del sistema come segue:

F = m × a → a = F / m

a = 12 N / 5 kg = 2,4 m/s²

Dopo aver trovato l'accelerazione del sistema, possiamo utilizzare nuovamente il secondo principio della dinamica di Newton per calcolare la tensione della corda. Per farlo, moltiplica l'accelerazione per la massa che la corda sta tirando. Per quanto riguarda T₂, il diagramma ci mostra che è responsabile solo della massa di m₂: T₂ = a × m₂. Dunque, T₂ = (2,4 m/s²) × (2 kg) = 4,8 N. D'altra parte, T₁ è la forza di tensione che tira sia il peso di m₁ che quello di m₂. Tuttavia, abbiamo già il valore di T₁, che è semplicemente uguale a T = 24,0 N. Pertanto, T₁ = 24,0 N.

Nel nostro esempio, se le due corde ne fossero una sola, potremmo paragonare questa configurazione a un sistema di pulegge. Una puleggia è una macchina semplice che sfrutta le forze di tensione delle corde per ottenere un guadagno meccanico. Per saperne di più sul guadagno meccanico e sulla tensione, puoi consultare il nostro calcolatore per la trasmissione a cinghia e il calcolatore per la lunghezza della cinghia, per un sistema a due pulegge.