Calcolatore per il Coefficiente Binomiale

Eccoti nel calcolatore per il coefficiente binomiale, dove avrai la possibilità di calcolare e imparare tutto sulla misteriosa formula "n su k". L'espressione indica il numero di combinazioni di k elementi di un insieme di n elementi e corrisponde al pulsante nCr di una calcolatrice.

Continua a leggere per scoprire che cos'è un binomio, il significato di "combinazione" e la differenza tra permutazione e combinazione. Troverai anche un esempio di calcolo di 4 su 2.

In matematica (più precisamente in algebra), un binomio è un polinomio con due termini (ecco da dove deriva il prefisso "bi-"). Ad esempio, le espressioni x + 1, xy - 2ab o x³z - 0,5y⁵ sono tutte binomi, ma x⁵, a + b - cd o x² - 4x² non lo sono (l'ultima ha due termini, ma possiamo semplificare l'espressione in -3x², che ne ha solo uno).

Ora che sappiamo cos'è un binomio, diamo un'occhiata più da vicino a un binomio elevato a una potenza:

(x² - 3)³.

Ci sono alcuni casi speciali di questa espressione — le formule di moltiplicazione di polinomi che forse conosci da scuola:

(a + b)² = a² + 2ab + b²,

(a - b)² = a² - 2ab + b².

Il polinomio che otteniamo sul lato destro è chiamato espansione binomiale di quello che avevamo tra le parentesi. Che tu ci creda o no, possiamo trovare le loro formule per qualsiasi potenza intera positiva. In generale, il teorema del binomio ci dice come si presenta questa espansione:

dove:

• $C_k$ — Numero di tutte le possibili combinazioni di $k$ elementi di un insieme di $n$ elementi.

Inoltre, per un dato n, questi numeri sono ordinatamente presentati per valori consecutivi di n nelle righe del cosiddetto triangolo di Tartaglia, dove una singola riga conta tutti i possibili sottoinsiemi dell'insieme (cioè la cardinalità dell'insieme di potenza). Visita il nostro calcolatore per il triangolo di Tartaglia 🇺🇸 per generare il triangolo di Tartaglia della dimensione che desideri.

Questo è un buon momento per scoprire il significato di "combinazione", come abbiamo già detto tante volte.

Immagina di essere uno studente universitario e di fare un pisolino durante una lezione. All'improvviso, l'insegnante ti riporta sulla Terra dicendoti: "Adesso sceglierò a caso i gruppi per i progetti di fine anno." Beh, a quanto pare dovrai lavorare un po', dopotutto.

Il problema è che c'è solo un ragazzo con cui vorresti lavorare al progetto. Se ci sono venti persone nel gruppo e l'insegnante vi divide in gruppi di quattro, qual è la probabilità che tu sia con il tuo amico?

Ogni possibile gruppo è un esempio di combinazione. In questo caso, una combinazione di quattro elementi di un insieme di venti elementi, o se preferisci, di quattro studenti di un gruppo di venti persone. Per essere più tecnici, scegliere una combinazione significa scegliere un sottoinsieme di un insieme più grande. L'aspetto più importante è che l'ordine degli elementi scelti non ha importanza. Dopo tutto, tutti i membri di un progetto di gruppo sono uguali (tranne quelli che non lavorano).

Il numero di combinazioni di k elementi di un insieme di n elementi è indicato da:

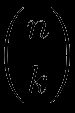
(come una frazione di n divisa per k ma senza la linea in mezzo) che si legge "n su k". Questo è anche il simbolo che appare quando scegliamo nCr su una calcolatrice (non il nostro calcolatore per il coefficiente binomiale, ma una calcolatrice tradizionale). Ad esempio,

è " 4 su 2", e

è "6 su 2". In alcuni libri di matematica, il coefficiente binomiale viene anche indicato con C(n,k), rendendolo una funzione di n e k. "E come faccio a calcolarlo?" Beh, è abbastanza facile. La formula di n su k è

n! / (k! × (n - k)!).

Il punto esclamativo è chiamato fattoriale. L'espressione n! è il prodotto dei primi n numeri naturali, cioè,

n! = 1 × 2 × 3 × ... × n.

Questo significa che, ad esempio, il 4 su 2 di cui sopra è:

4! / (2! × (4 - 2)!) = (1 × 2 × 3 × 4) / (1 × 2 × 1 × 2) = 6,

e 6 su 2 è:

6! / (2! × (6 - 2)!) = (1 × 2 × 3 × 4 × 5 × 6) / (1 × 2 × 1 × 2 × 3 × 4) = 15.

Per saperne di più sui fattoriali, visita il nostro calcolatore per il fattoriale 🇺🇸!

Quindi possiamo scegliere due elementi da un insieme di quattro con un totale di sei combinazioni, e da un insieme di sei, con quindici combinazioni.

Prima di andare avanti, diamo un'ultima occhiata alla formula di n su k. Possiamo ricavarne una proprietà simmetrica piuttosto interessante.

Se prendiamo n su n - k, allora otterremo:

n! / ((n - k)! × (n - (n - k))!) = n! / ((n - k)! × k!),

che è la stessa cosa di n su k (dato che la moltiplicazione è commutativa). In altre parole, abbiamo

o C(n,k) = C(n,n-k) nell'altra notazione.

Nella sezione precedente, abbiamo visto che cos'è un fattoriale. In combinatoria, esso indica il numero di permutazioni. Una permutazione di lunghezza n significa mettere n elementi in un certo ordine. Ad esempio, se abbiamo tre espressioni di gattini carini, ad esempio 😹, 😻 e 🙀, possiamo ordinarli in sei modi diversi:

(😹, 😻, 🙀)

(😹, 🙀, 😻)

(😻, 😹, 🙀)

(😻, 🙀, 😹)

(🙀, 😹, 😻)

(🙀, 😻, 😹).

Osserva che questo concorda con quanto ci dice il fattoriale:

3! = 3 × 2 × 1 = 6.

Visita il nostro calcolatore per la permutazione 🇺🇸 approfondire questo argomento.

Nota che esiste un altro modo di visualizzare questo concetto: scegliamo il primo elemento su tre (3 opzioni), il secondo sui due rimanenti (perché ne abbiamo già scelto uno) e il terzo, cioè quello rimasto (perché ne abbiamo già scelti due). Moltiplichiamo il numero di scelte: 3 × 2 × 1 = 6, e otteniamo il fattoriale.

Quando mettiamo permutazione e combinazione a confronto, la parola chiave è ordine. Come abbiamo detto nella sezione precedente, una combinazione consiste nel selezionare alcuni elementi da una collezione più grande. In sostanza, diciamo quali elementi scegliamo, ma non quale sia il primo, il secondo, ecc. Essi formano un insieme.

Una permutazione, invece, mette gli elementi in un ordine fisso, uno dopo l'altro, rendendolo una sequenza piuttosto che un insieme. Inoltre, una permutazione utilizza tutti gli elementi dell'insieme, mentre una combinazione ne sceglie solo alcuni.

Per fare un esempio, mettiti ancora una volta nei panni di uno studente universitario. Quando l'insegnante ha scelto il gruppo per te, ha scelto una combinazione. E quando arriva il momento di presentare il tuo progetto e ciascuno di voi deve rispondere a una domanda, si applica la permutazione (determinando l'ordine in cui vengono poste le domande). E sappiamo tutti quanto sia importante l'ordine per il tuo voto finale.

I coefficienti binomiali sono una delle sequenze di numeri più importanti della matematica discreta e della combinatoria. Appaiono molto spesso nei calcoli di statistica e probabilità e sono forse i più importanti nella distribuzione binomiale (compresa la distribuzione binomiale negativa 🇺🇸). Questo significa che solo i matematici smanettoni ne hanno una reale utilità?

Niente affatto! Ogni gioco d'azzardo si basa sul caso e i coefficienti binomiali ne sono un elemento fondamentale. Un lancio di una moneta è l'esempio più semplice, che puoi calcolare con il nostro calcolatore per il lancio della moneta. Tuttavia, facciamo un passo avanti e soffermiamoci sul poker.

Ti è mai capitato di chiederti "Perché alcune mani nel poker hanno più valore di altre?" Semplicemente perché sono più rare (a meno che qualcuno non stia barando, ma abbiamo visto abbastanza serie TV di gangster per sapere che di solito è una cattiva idea).

In un mazzo normale ci sono 52 carte e nel poker tradizionale (5-card draw) un giocatore riceve cinque carte. Il nostro calcolatore per il coefficiente binomiale e la formula n su k (nel nostro caso, n = 52 e k = 5) ci dice che questo si traduce in 2 598 960 mani possibili in una partita di poker. Un bel po', non credi? E ora considera la migliore mano possibile — una scala reale di fiori (asso, re, regina, fante e 10). Questa mano può verificarsi solo in un caso — quando si ottengono esattamente quelle carte. Questo significa che c'è una probabilità pari a 1 su 2 598 960 di averla. Forse giocare tutti i tuoi risparmi su questa minuscola possibilità non è la scelta migliore.

Facciamo un altro esempio — un full (tris e coppia). Questa volta ci sono notevolmente più possibilità. Dopo tutto, una qualsiasi delle 13 carte di un seme può essere il tris, e la coppia si trova in una delle altre 12 carte (non può avere lo stesso valore del tris). Inoltre, il tris è presente solo in tre dei quattro simboli delle carte e, allo stesso modo, la coppia è presente solo in due.

Ed è qui che ricordiamo il significato di "combinazione"! Dobbiamo scegliere tre simboli su quattro per il tris e una combinazione di due su quattro per la coppia. La formula n su k si traduce in 4 su 3, e 4 su 2, e il calcolatore per il coefficiente binomiale li considera rispettivamente 4 e 6. In definitiva, se ora moltiplichiamo i numeri che abbiamo ottenuto, scopriremo che ci sono

13 × 12 × 4 × 6 = 3744

mani possibili che danno un full. Beh, non sono molte rispetto a tutte le possibilità, ma almeno è 3744 volte più probabile della scala reale di fiori.

Tuttavia, suggeriamo di risparmiare regolarmente denaro come tecnica di investimento migliore rispetto al gioco d'azzardo.