Calcolatore per Esagoni

Benvenuto nel calcolatore per esagoni, uno strumento utile per trattare qualsiasi esagono regolare. La forma dell'esagono è una delle forme più popolari in natura, dai modelli a nido d'ape alle piastrelle esagonali per gli specchi — i suoi usi sono quasi infiniti. Qui ti spieghiamo non solo perché questo poligono a 6 lati è così popolare, ma anche come disegnare correttamente i lati di un esagono. Rispondiamo anche alla domanda "cos'è un esagono?" utilizzando la definizione di esagono.

Con il nostro calcolatore per esagoni, potrai esplorare molte proprietà geometriche e calcoli, incluso come trovare l'area di un esagono, oltre a insegnarti ad utilizzare il calcolatore per semplificare qualsiasi analisi che coinvolga questa forma a 6 lati.

Non deve sorprendere che l'esagono (noto anche come "poligono a 6 lati") abbia esattamente sei lati. Questo fatto è vero per tutti gli esagoni, poiché è la loro caratteristica distintiva. La lunghezza dei lati può variare anche all'interno dello stesso esagono, tranne quando si tratta dell'esagono regolare, in cui tutti i lati devono avere la stessa lunghezza.

Ci addentreremo un po' di più in questa forma più avanti, quando ci occuperemo di come trovare l'area di un esagono. Per ora, è sufficiente dire che l'esagono regolare è il più comune tra i poligoni a 6 lati e quello che si trova più spesso in natura.

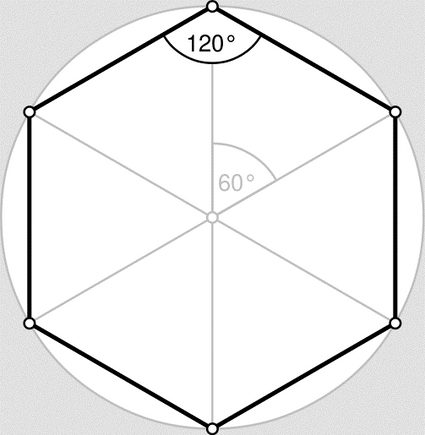
Ci sarà un'intera sezione dedicata alle importanti proprietà della forma dell'esagono regolare, ma prima dobbiamo conoscere la risposta tecnica a; "Che cos'è un esagono?" Rispondere a questa domanda ci aiuterà a capire i trucchi che possiamo usare per calcolare l'area di un esagono senza usare la formula dell'area dell'esagono alla cieca. Questi trucchi prevedono l'utilizzo di altri poligoni come quadrati, triangoli e persino parallelogrammi.

Come abbiamo già detto, l'esagono regolare deve avere tutti i lati di uguale lunghezza e tutti gli angoli interni devono essere uguali. La lunghezza di ciascun lato è ugualmente valida (a patto che sia condivisa da tutti e 6 i lati!), quindi calcolare il perimetro di un esagono è così semplice che non hai nemmeno bisogno del calcolatore per il perimetro di un poligono 🇺🇸. Basta calcolare:

• Perimetro = 6 × lato.

Gli angoli di un esagono arbitrario possono avere qualsiasi valore, ma devono essere tutti pari a 720º (puoi facilmente convertirli in altre unità di misura utilizzando il nostro convertitore di angoli 🇺🇸). Poiché l'esagono regolare richiede che tutti gli angoli siano uguali, ne consegue che ogni singolo angolo debba essere di 120º. Questo fatto si rivela di estrema importanza quando parliamo della popolarità della forma dell'esagono in natura. Sarà utile anche quando spiegheremo come trovare l'area di un esagono regolare. Lo useremo anche per trovare la formula dell'area degli esagoni regolari.

Vediamo ora come trovare l'area di un esagono utilizzando diversi trucchi. Il modo più semplice è utilizzare il nostro calcolatore per esagoni, che include uno strumento di conversione dell'area. Per coloro che vogliono sapere come farlo a mano, spiegheremo come trovare l'area di un esagono regolare con e senza la formula dell'area dell'esagono. La formula dell'area di un poligono è sempre la stessa, indipendentemente dal numero di lati, purché si tratti di un poligono regolare:

• Area = apotema × perimetro / 2.

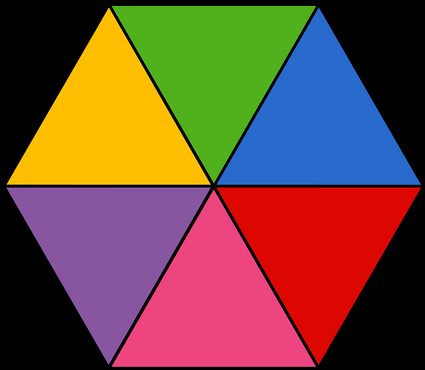
Ricordiamo che l'apotema è la distanza tra il punto medio di un lato e il centro. Puoi considerarlo come l'altezza del triangolo equilatero formato da un lato e due raggi dell'esagono (ciascuna delle aree colorate nell'immagine precedente). In alternativa, si può anche pensare all'apotema come alla distanza tra il centro e un lato qualsiasi dell'esagono, dato che la distanza euclidea è definita utilizzando una linea perpendicolare.

Se non ricordi la formula, puoi sempre pensare al poligono a 6 lati come a un insieme di 6 triangoli. Nel caso dell'esagono regolare, questi triangoli sono triangoli equilateri. Questo fatto rende molto più facile calcolare la loro area rispetto ai triangoli isosceli o ai triangoli 45 45 90 come nel caso di un quadrato.

Nel caso del triangolo equilatero, tutti i lati hanno la stessa lunghezza, che è la lunghezza del lato dell'esagono che è stato formato. Lo chiameremo a. L'altezza di un triangolo sarà h = √3/2 × a, che è il valore esatto dell'apotema in questo caso. Ti ricordiamo che √ significa radice quadrata. Con questa premessa, possiamo iniziare a fare i conti:

• A₀ = a × h/2;
• = a × √3/2 × a/2; e
• = √3/4 × a².

Dove A₀ indica l'area di ciascuno dei triangoli equilateri in cui abbiamo diviso l'esagono. Dopo aver moltiplicato quest'area per sei (perché abbiamo 6 triangoli), otteniamo la formula dell'area dell'esagono:

• A = 6 × A₀ = 6 × √3/4 × a²;

• A = 3 × √3/2 × a²;

• = (√3/2 × a) × (6 × a) /2; e

• = apotema × perimetro /2.

Speriamo che tu riesca a capire come si arriva alla stessa formula dell'area dell'esagono di cui abbiamo parlato prima.

Puoi anche giocare con altre forme diverse. Ad esempio, supponiamo di dividere l'esagono a metà (da vertice a vertice). In questo caso otterrai due trapezi e potrai calcolare l'area dell'esagono come la loro somma. Puoi anche combinare due triangoli adiacenti per costruire un totale di 3 rombi diversi e calcolare l'area di ciascuno di essi separatamente. Puoi anche scomporre l'esagono in un grande rettangolo (usando le diagonali corte) e in 2 triangoli isosceli!

Sentiti libero di giocare con forme e calcolatori diversi per vedere quali altri trucchi ti vengono in mente. Prova a utilizzare solo triangoli rettangoli o magari anche triangoli rettangoli speciali per calcolare l'area di un esagono!

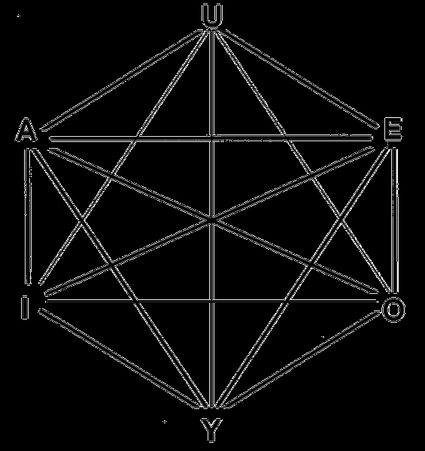
Il numero totale di diagonali dell'esagono è pari a 9 — tre di queste sono le diagonali lunghe che attraversano il punto centrale, mentre le altre sei rappresentano la cosiddetta "altezza" dell'esagono.
Il nostro calcolatore per esagoni può anche risparmiarti alcuni noiosi calcoli sulla lunghezza delle diagonali dell'esagono. Ecco come calcolare i due tipi di diagonali:

• Diagonali lunghe — Attraversano sempre il punto centrale dell'esagono. Come puoi notare dall'immagine qui sopra, la lunghezza di una diagonale di questo tipo è uguale alla lunghezza di due spigoli:

  D = 2 × a.

• Diagonali corte — Non attraversano il punto centrale. Si costruiscono unendo due vertici, lasciandone esattamente uno in mezzo. La loro lunghezza è pari a d = √3 × a.

Un'altra coppia di valori importanti per un esagono sono i raggi dei cerchi circoscritto e inscritto. Il cerchio circoscritto è un cerchio contiene tutti i vertici dell'esagono regolare. Il cerchio inscritto è il cerchio più grande che può essere disegnato all'interno di un esagono.

• Raggio del cerchio circoscritto — Per trovare il raggio di un cerchio circoscritto all'esagono regolare, devi determinare la distanza tra il punto centrale dell'esagono (che è anche il centro del cerchio) e uno qualsiasi dei vertici. È semplicemente uguale a R = a; e

• Raggio del cerchio inscritto — Il raggio di un cerchio inscritto in un esagono regolare è uguale alla metà della sua altezza, che è anche l'apotema: r = √3/2 × a.

Ora esploreremo un mondo più pratico e meno matematico — come disegnare un esagono. Per un esagono casuale (irregolare), la risposta è semplice; disegna una qualsiasi forma a 6 lati in modo che sia un poligono chiuso e il gioco è fatto. Ma per un esagono regolare, le cose non sono così semplici poiché dobbiamo assicurarci che tutti i lati siano della stessa lunghezza.

Per ottenere un risultato perfetto, avrai bisogno di un compasso da disegno. Disegna un cerchio e, con lo stesso raggio, inizia a fare dei segni lungo di esso. Disegna un cerchio con il compasso partendo da un punto a caso e poi fai il segno successivo usando il precedente come punto di ancoraggio. Alla fine otterrai 6 segni e se li unisci con le linee rette, otterrai un esagono regolare. Puoi vedere un processo simile nell'animazione qui sopra.

Il calcolatore per esagoni ti permette di calcolare diversi parametri interessanti della forma a 6 lati che di solito chiamiamo esagono. L'utilizzo di questo calcolatore è il più semplice possibile con un solo parametro necessario per calcolare tutti gli altri e include uno strumento di conversione della lunghezza per ognuno di essi.

Abbiamo già parlato di tutti i parametri del calcolatore, ma per motivi di chiarezza e completezza li esamineremo brevemente:

• Area — Superficie bidimensionale racchiusa dalla forma dell'esagono;
• Lato — Distanza tra un vertice e il successivo;
• Perimetro — Somma delle lunghezze di tutti i lati dell'esagono;
• Diagonale lunga — Distanza da un vertice a quello opposto;
• Diagonale corta — Distanza tra due vertici che hanno un altro vertice tra loro;
• Raggio del cerchio circoscritto — Distanza dal centro a un vertice (uguale al raggio dell'esagono); e
• Raggio del cerchio inscritto — Uguale all'apotema.

Tutti amano una bell'applicazione reale della teoria e gli esagoni sono sicuramente uno dei poligoni più utilizzati al mondo. Partendo dagli utilizzi umani, l'impiego più semplice (e probabilmente meno entusiasmante) è quello delle piastrelle esagonali per i pavimenti. L'esagono è una forma eccellente perché si adatta perfettamente a sè per coprire qualsiasi area desiderata. Se sei interessato a questo tipo di utilizzo, ti consigliamo di utilizzare il calcolatore per pavimentazioni e il calcolatore per l'area del rettangolo che sono strumenti eccellenti per questo scopo.

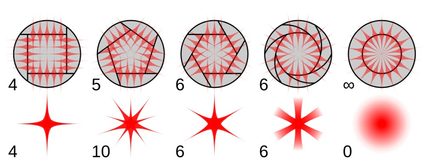
Il caso seguente è comune a tutti i poligoni, ma è comunque interessante da esplorare. Nella fotografia, l'apertura del sensore ha quasi sempre una forma poligonale. Questa parte della fotocamera è chiamata apertura e determina molte proprietà e caratteristiche delle immagini prodotte da una fotocamera. La più inaspettata è la forma degli oggetti molto luminosi (puntiformi) dovuta all'effetto chiamato reticolo di diffrazione, illustrato nell'immagine qui sopra.

Uno degli usi più importanti degli esagoni nell'era moderna, strettamente legato a quello di cui abbiamo parlato nella fotografia, è quello astronomico. Uno dei maggiori problemi che incontriamo quando osserviamo le stelle lontane è la loro fievolezza nel cielo notturno. Questo perché, nonostante siano oggetti molto luminosi, sono così lontane che solo una minima parte della loro luce ci raggiunge; puoi saperne di più nel nostro calcolatore di luminosità 🇺🇸. Inoltre, a causa di effetti relativistici (simili alla dilatazione temporale e alla contrazione delle lunghezze), la loro luce arriva sulla Terra con un'energia inferiore a quella con cui è stata emessa. Questo effetto è chiamato spostamento verso il rosso.

Il risultato che otteniamo è una piccola quantità di energia con una lunghezza d'onda maggiore di quella che vorremmo. Il modo migliore per contrastare questa situazione è costruire telescopi sempre più grandi. Il problema è che realizzare una lente o uno specchio in un unico pezzo grande un paio di metri è quasi impossibile, per non parlare dei problemi logistici. La soluzione è costruire uno specchio modulare utilizzando piastrelle esagonali come quelle che puoi vedere nelle immagini qui sopra.

La realizzazione di uno specchio così grande migliora la risoluzione angolare del telescopio e il fattore di ingrandimento grazie alle proprietà geometriche di un "telescopio Cassegrain". Quindi possiamo dire che grazie agli esagoni regolari possiamo vedere meglio, più lontano e più chiaramente di quanto avremmo mai potuto fare con lenti o specchi monoblocco.

Sapevi che esistono anche le trapunte a esagoni? Scopri di più con il calcolatore per trapunte esagonali 🇺🇸 di Omni!

Il motivo a nido d'ape è composto da esagoni regolari disposti uno accanto all'altro. Essi riempiono completamente l'intera superficie su cui si estendono, quindi non ci sono buchi tra di loro. Questo motivo ad alveare non compare solo negli alveari (sorpresa!) ma anche in molte altre istanze naturali. In effetti, è così diffusa che si potrebbe dire la forma predefinita quando sono in gioco forze contrastanti, in quanto le sfere non sono possibili a causa della natura del problema.

Dagli alveari delle api alle fessure delle rocce, passando per la chimica organica (persino nei mattoni della vita; le proteine), gli esagoni regolari sono la forma poligonale più comune che esiste in natura. E c'è una ragione per questo; gli angoli degli esagoni. L'angolo di 120º è il più stabile dal punto di vista meccanico e, casualmente, è anche l'angolo in cui i lati si incontrano ai vertici quando mettiamo gli esagoni uno accanto all'altro. Per una descrizione completa dell'importanza e dei vantaggi degli esagoni regolari, ti consigliamo di guardare questo video con sottotitoli in italiano.

Il modo in cui gli angoli di 120° distribuiscono le forze (e quindi le sollecitazioni) tra i 2 lati dell'esagono lo rende una forma geometrica molto stabile e meccanicamente efficiente. Questo è un vantaggio significativo degli esagoni. Un'altra importante proprietà degli esagoni regolari è che possono riempire una superficie senza avere spazi vuoti tra loro (come i triangoli e i quadrati regolari). Inoltre, la forma regolare a 6 lati ha il perimetro più piccolo per l'area più grande tra questi poligoni-mattonella il che la rende molto efficiente.

Un esempio affascinante in questo video è quello delle bolle di sapone. Quando si crea una bolla utilizzando dell'acqua, sapone e un po' del proprio respiro, questa ha sempre una forma sferica. Questo risultato è dovuto al fatto che il volume di una sfera è il più grande di qualsiasi altro oggetto a parità di superficie.

Tuttavia, quando disponiamo le bolle su una superficie piana, la sfera perde il suo vantaggio di efficienza poiché la sezione di una sfera non può coprire completamente uno spazio 2D. La forma migliore in termini di rapporto volume-superficie è anche la migliore per bilanciare la tensione tra le bolle che si crea sulla superficie delle stesse. Stiamo parlando, ovviamente, del nostro magnifico esagono.

Le bolle rappresentano un modo interessante per visualizzare i vantaggi di un esagono rispetto ad altre forme, ma non è l'unico modo. In natura, come abbiamo detto, ci sono molti esempi di formazioni esagonali, per lo più dovute a tensioni e stress nel materiale. Purtroppo non possiamo analizzarli tutti nel dettaglio. Possiamo però nominare alcuni luoghi in cui si possono trovare modelli esagonali regolari in natura:

• Alveari;
• Composti organici;
• Bolle;
• Formazioni rocciose (come quelle di Giant);
• Occhi di insetti; e
• Etc.