Calcolatore per la Pendenza di una Retta

Il calcolatore per la pendenza di una retta ti mostrerà come trovare l'equazione di una retta a partire da un punto sulla retta e dalla pendenza della retta. Presto saprai cos'è l'equazione della retta con la pendenza e imparerai come si differenzia dall'equazione della retta con l'intercetta. Abbiamo anche ideato due esercizi e ti spiegheremo come risolverli nell'ultimo paragrafo.

Iniziamo dalle basi e parliamo di cosa sia la pendenza.

La pendenza, nota anche come gradiente, è l'indicatore della ripidità di una linea. Se è positiva, significa che la linea sale. Se è negativa, la linea scende. Se è uguale a zero, la linea è orizzontale.

Puoi trovare la pendenza tra due punti stimando l'rapporto salita su percorso, ovvero la differenza di altezza su una distanza tra due punti.

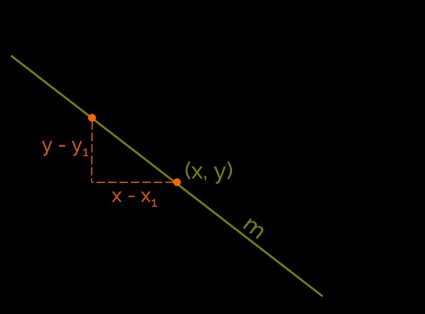
Quindi, la formula della pendenza è:

m = variazione di y / variazione di x = (y - y₁) / (x - x₁)

L'equazione della pendenza è un'equazione della pendenza riorganizzata.

Per trovare il gradiente di funzioni non lineari, puoi utilizzare il calcolatore del tasso di variazione medio.

Esiste più di un modo per formare l'equazione di una retta. La pendenza di una retta è una forma di equazione lineare in cui ci sono tre numeri caratteristici — due coordinate di un punto sulla retta e la pendenza della retta. L'equazione è la seguente:

dove:

• $\small x_1, y_1$ sono le coordinate di un punto; e
• $\small m$ è la pendenza.

Vedi la somiglianza con la formula della pendenza? Quello che forse non sai è che non è l'unico modo per formare l'equazione di una retta. La formula più diffusa è quella dell'intercetta della pendenza:

dove:

• $\small m$ è la pendenza; e
• $\small b$ è l'intercetta dell'asse y.

In realtà, questa non è altro che una forma più precisa della pendenza di una retta. Una retta intercetta l'asse y in un punto (0, b). Se scegli questo punto — (0, b) — come punto da utilizzare nella pendenza di una retta dell'equazione, otterrai:

$\small y - b = m \times (x - 0)$, che è la stessa cosa di $\small y = m \times x + b$.

Nei due grafici qui sotto puoi vedere la stessa funzione, solo descritta con due forme diverse di equazione lineare:

Per imparare a trovare l'intercetta x e l'intercetta y di una retta, visita il nostro calcolatore per l'intercetta x e y 🇺🇸.

Vediamo due esercizi per capire meglio l'argomento.

La pendenza di una retta è 2. Essa passa per il punto A(2, -3). Qual è l'equazione generale della retta?

1. Identifica le coordinate del punto:
   • x₁ = 2
   • y₁ = -3;
2. Identifica la pendenza:
   • m = 2;
3. Inserisci i valori nella formula del modulo della pendenza:
   • $\small y - y_1 = m (x - x_1)$
   • $\small y - (-3) = 2(x - 2)$;
4. Semplifica per ottenere l'equazione generale:
   • $\small y = 2x - 4 -3$
   • $\small 0 = 2x - y - 7$.
   Ed ecco la risposta. Ora puoi verificare il risultato con il nostro calcolatore per la pendenza di una retta.

Risolviamo un esercizio con un argomento più riconoscibile.

Supponiamo che tu abbia preso un cucciolo. Quando l'hai preso, pesava 4 chili. Ogni giorno è cresciuto di 0,2 e dopo 30 giorni pesava 10 chili. Trova l'equazione generale della crescita del cucciolo.

1. La pendenza è la variazione di peso al giorno: m = 0,2;

2. Il punto caratteristico è di 10 chili al 30° giorno: (x₁, y₁) = (30, 10);

3. Ora inserisci i valori nella formula del punto di pendenza:

   $\small y - 10 = 0,2 \times (x - 30)$;

4. Semplifica l'equazione per ottenere l'equazione generale:

   $\small 0 = 0.2x - y + 4$.

Ed ecco fatto! Ci auguriamo che il nostro calcolatore per la pendenza di una retta ti sia piaciuto!

Se ti viene data la pendenza di una retta, puoi ottenere l'intercetta della pendenza seguendo questi passaggi:

1. Determina la direzione della pendenza:

   y - b = m(x - a);

2. Espandi il lato destro:

   y - b = mx - ma;

3. Aggiungi b a entrambi i lati:

   y = mx - ma + b; e

4. Questa è la formula dell'intercetta della pendenza! La pendenza è m e l'intercetta è -ma + b.

L'intercetta y di una retta con la pendenza y - b = m(x - a) è data dalla formula intercetta = b - ma. Ad esempio, per la retta y - 1 = 2(x - 3) si ottiene l'intercetta 1 - 6 = -5.

Se la pendenza è zero, la formula della pendenza si riduce a y - b = 0. Questa equazione descrive una linea orizzontale che attraversa l'asse verticale a y = b.

Sì! Prendiamo la retta con formula di intercetta della pendenza y = mx + b. Scriviamo la formula della pendenza per il punto (0, b). Otteniamo y - b = m(x - 0), che è la stessa (fino alla banale trasformazione di spostare b sul lato destro) della formula dell'intercetta della pendenza.