Hypotenuse Calculator
With this hypotenuse calculator, you will quickly find the longest side of a right triangle. If you want to know the hypotenuse of a right triangle and how to find it, you'll discover the answers below, along with a simple example to clarify things. We also present the hypotenuse of a triangle formula, so you know the equation behind our calculator.
Don't wait any longer; give this hypotenuse calculator a try!
How to use this hypotenuse calculator
The following instructions will show you how to use this calculator with ease:
-
Select which set of parameters is known. You can choose between:
-
Two sides.
-
An angle and one side.
-
Area and one side.
-
-
Enter the known parameters, following the labels in the diagram. To input a parameter in a different unit than the default option, click on the unit, change it, and then enter the parameter value.
-
The tool will immediately calculate the hypotenuse (and any other missing dimensions). Click on the unit to change it to anyone you like.
Consider a right triangle with angle α = 60° and side a = 5 cm. First, we select the option angle and one side and enter these values. Instantly, the calculator determines that:
- Side b = 2.887 cm;
- Angle β = 30°; and
- Hypotenuse c = 5.774 cm.
The calculator is usable in reverse, too. Suppose you must find an unknown side using the hypotenuse (13 cm) and a known side (12 cm). Select two sides as the given parameters, and enter the hypotenuse c = 13 cm and side a = 12 cm. Instantly, you can learn that side b = 5 cm.
The following article explains what the hypotenuse is and how it is calculated using different parameters. It is fun and informative, so we recommend you read it to internalize this concept well.
What is the hypotenuse of a triangle?
A hypotenuse is the longest side of a right triangle. It's the side that is opposite to the right angle (90°). Hypotenuse length may be found, for example, from the Pythagorean theorem. You can learn more about this in our pythagorean theorem calculator.
Hypotenuse of a triangle formula
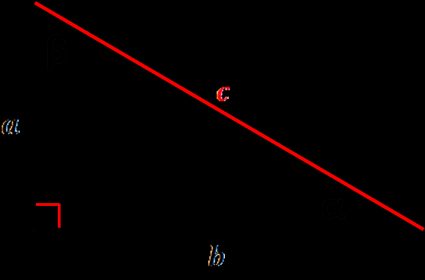
This hypotenuse calculator has a few formulas implemented — this way, we made sure it fits different scenarios you may encounter. You can find the hypotenuse:
- Given two right triangle legs
Use the Pythagorean theorem to calculate the hypotenuse from the legs of the right triangle. Take a square root of the sum of their squares:
c = √(a² + b²)

- Given an angle and one leg
c = a / sin(α) = b / sin(β), explained in our law of sines calculator.
- Given the area and one leg
As the area of a right triangle is equal to a × b / 2, then
c = √(a² + b²) = √(a² + (area × 2 / a)²) = √((area × 2 / b)² + b²).
To learn more about calculations involving right triangles, visit our area of a right triangle calculator and the right triangle side and angle calculator.
Ladder example — How to find the hypotenuse of a right triangle with this hypotenuse calculator

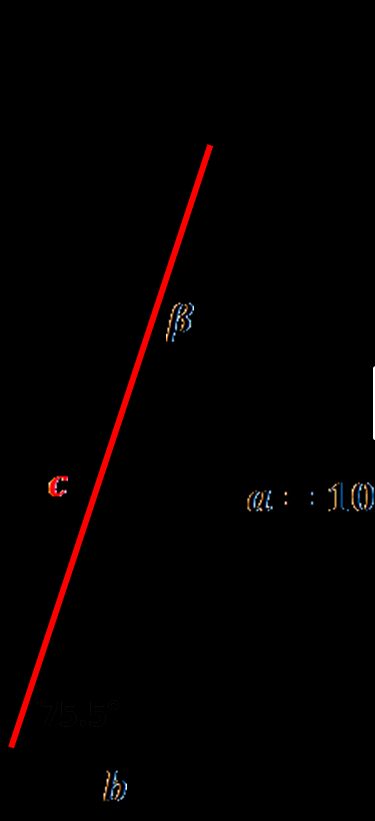
Let's calculate how long the ladder should be if we want to rescue a kitten from a 10 ft roof. The calculator helps to find the ladder length from the ground to the edge of the roof, but don't forget about the part of the ladder which should extend over the edge!
- Choose the option needed for your calculations. We know that our roof is 10 ft in height and that the safest angle for a ladder is ~75.5°. From the dropdown list of the given box, select the option: angle ∡ and one side.
- Change the units to feet.
-
Enter the given values. Our leg a is 10 ft long, and the α angle between the ladder and the ground equals 75.5°.
-
Ladder length, our right triangle hypotenuse, appears! It's equal to 10.33 ft.
The angle β = 14.5° and leg b = 2.586 ft are displayed as well. The second leg is also an important parameter, as it tells you how far you should place the ladder from the wall (or rather from a roof edge). The general principle to remember is a 4:1 rule – for every four feet of vertical height, the ladder foot should move one foot from the wall.
Creating the hypotenuse calculator
I'm Hanna, a long-time creator at Omni Calculator, having made numerous useful scientific tools besides this one that resonate and help a wide range of people every day! The idea for this calculator came to me while I was calculating the correct length for a ladder to climb up to my roof. Struck by the ubiquitousness of right triangles in our daily lives, I was determined to make this tool so it may help everyone!
We at Omni exercise extreme care to ensure the quality of our content so that it is as accurate and reliable as possible. Each tool is peer-reviewed by a trained expert and then proofread by a native speaker. You can learn more about our standards in our page.
FAQs
How do I find hypotenuse with sin?
- Perform the sin operation on the angle (not the right angle).
- Divide the length of the side opposite the angle used in step 1 by the result of step 1.
- The result is the hypotenuse.
Is the hypotenuse always the longest side?
Yes, the hypotenuse is always the longest side, but only for right-angled triangles. For isosceles triangles, the two equal sides are known as the legs, while in an equilateral triangle, all sides are known simply as sides.
How do I find the hypotenuse adjacent and opposite?
- Find the longest side and label it the hypotenuse.
- You can only find the adjacent and opposite sides if you choose one angle less than 90 degrees.
- The adjacent is the side that forms the angle of choice along with the hypotenuse.
- The opposite is the side that does not form the angle of choice.
How do you find the altitude of a hypotenuse?
- Draw the altitude of the hypotenuse on the triangle. The two new triangles you have created are similar to each other and the main triangle.
- Divide the length of the shortest side of the main triangle by the hypotenuse of the main triangle.
- Multiply the result by the length of the remaining side to get the length of the altitude.
- Alternatively, the angles within the smaller triangles will be the same as the angles of the main one, so you can perform trigonometry to find it another way.
What should I do if the hypotenuse is the opposite?
If the hypotenuse is the opposite, then you are considering the wrong angle — you cannot use trigonometry with the right angle of a triangle. Consider one of the other angles. This is the adjacent angle. The opposite will be the side that does not form that angle.
How do I construct a line perpendicular to the hypotenuse?
- Acquire a pair of compasses, a ruler, and a pen or pencil.
- Set your pair of compasses to the length of the hypotenuse (or any length, as long as it stays constant).
- Draw a circle that has its center at one of the ends of the hypotenuse.
- Draw another circle with its center at the other end of the hypotenuse.
- Draw a line joining the two points where these circles meet. This line is perpendicular to the hypotenuse.
How do I find the hypotenuse of isosceles right triangle?
- Find the length of one of the non-hypotenuse sides.
- Square the length of the side.
- Double the result of the previous step.
- Square root the result of step 3. This is the length of the hypotenuse.
What is the hypotenuse angle theorem?
The hypotenuse angle theorem is a way of testing if two right-angled triangles are congruent or not. It states that if two right-angled triangles have a hypotenuse and an acute angle that is the same, they are congruent.
Where does the word hypotenuse come from?
The word hypotenuse comes from the Ancient Greek hypoteinousa, meaning ‘stretching under (a right angle)’. This, in turn, comes from hypo- ‘under’ and teinein ‘to stretch’. Another thing we have to thank the Ancient Greeks for!
How do I solve a right triangle with only the hypotenuse?
You cannot solve a right-angled triangle with only the hypotenuse. This is because the other two sides and angles are still undefined, so the triangle can still have many forms.
