Tangent Calculator

This tangent calculator will help you to find the tangent of any angle you want. Just enter the angle in degrees or radians, and the tangent will appear in no time. If you want to understand what a tangent is, and you're curious about the tangent definition or the tangent formula derivation, keep reading! Also sin over cos meme is waiting for you down there.

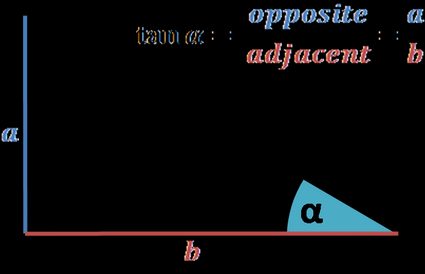
Tangent is one of the three most common trigonometric functions (along with sine and cosine). It may be defined as:

The ratio of the sides: opposite and adjacent to an angle in a right-angled triangle.

Check out our ratio calculator to learn more about ratios!

BUT! There's also another geometric concept named tangent. It's a line or plane that touches a curve or curved surface at a point, but if extended, it doesn't cross it at that point.

The word tangent comes from the Latin tangere which means 'to touch'. And our trigonometric function name also comes from that meaning! Have a look at the picture below:

Draw a unit circle. Point C is the intersection of the line containing the radius and the line x = 1. Then, tan(α) is simply the y-coordinate of point C.

The tangent of an angle may also be defined as its sine divided by its cosine. But why is it so? Have a look at the picture of a unit circle, and all should be clear:

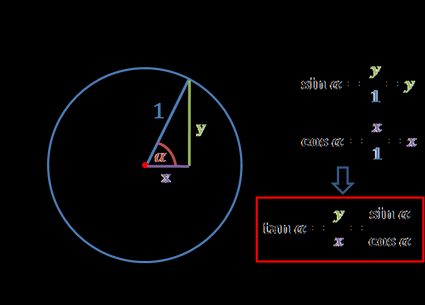
Knowing the definition of sine – opposite over hypotenuse – we can find out that for the right triangle from the image, the sin(α) = y. Analogically, cosine may be defined as adjacent over hypotenuse, so in our case, it's equal to x. Then, in the previous section, you learned that the tangent is equal to opposite over adjacent side. So, for our example, tan(α) = y/x, and that can be substituted by the sine and cosine of our angle of interest to get the final formula:

tan(α) = sin(α) / cos(α)

Not such a long time ago, you could find math jokes on the Internet – sin over cos memes. We're pretty sure that after reading this paragraph, you'll get this one!

What about tangerine 🍊? Tango 🎶? Titanic 🚢? Or even satanism? Think about other words which could make such a rebus!

The law of tangents describes the relationship between the tangent of two angles of a triangle and the lengths of the opposite sides. Specifically, it states that:

(a - b) / (a + b) = tan(0.5(α - β)) / tan(0.5(α + β))

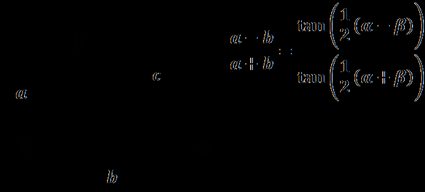
Although the law of tangents is not as popular as the law of sines or the law of cosines, it may be useful when we have given:

• Two sides and the angle between them; and
• Two angles and a side.

All you need to do is type one value into the calculator – the angle, in radians or degrees. To change between units, click on the unit name and choose from a drop-down list. Then, you'll see the result immediately – the tangent value of your angle of interest.

Remember that tan(α) may be undefined. This situation occurs when cos(α) is 0 because we can never divide by zero (other explanation: the lines will be parallel, so they'll never cross each other, and they won't form the point C).