Barn-Pole Paradox

The barn-pole paradox tricks you into believing two different and contradicting scenarios depending on the chosen frame of reference. In this exhaustive article, we will learn:

• What is the barn-pole paradox;
• The barn-pole paradox from the barn's perspective;
• The paradox as seen from a relativistic pole's point of view; and
• How to resolve the barn-pole paradox: solution thanks to the properties of simultaneity in relativity.

What are you waiting for? In relativity, you may have to wait quite a long time, so you better jump into this paradox right away!

Our daily life is relatively slow: unless you are a fighter jet pilot or an astronaut, you will barely brush a thousand kilometers per hour during the cruising phase of flight (maybe with some strong tailwinds). Most people you know, if not all, share this world with you: more or less, all your frames of reference move at the same speed. The Universe, however, carries a much ampler spectrum of speeds! There is just a limit out there: the speed of light, $c$.

The speed of light is the speed of propagation of electromagnetic radiation: as this radiation can be thought of as made of photons, massless particles, nothing can go faster than this (in the vacuum, at least), lest we find particles with negative mass! Once we start approaching this speed, all sorts of phenomena appear to ensure that physics doesn't break. Among these phenomena, we report:

• Time dilation: the faster an object moves, the slower time would flow compared to a stationary reference system. The clocks in a fast-moving spaceship would look slowed down, eventually freezing for speeds approaching $c$.

• Length contraction: to make up for a longer time, if an object moves at a constant speed, its length will contract, eventually shrinking to nothing for objects moving an iota away from the $c$.

This intimate connection between space and time allows us to interpret time as the fourth dimension of relativity. Thanks to this, we can define a set of operations that can move us from one inertial frame of reference (meaning that it moves at constant speed) to another: the Lorentz transformations. In the following sections, we will need the Lorentz transformation for time:

where:

• $\gamma$ — Lorentz factor (we will meet it soon);
• $t$ — Time in the observer's reference frame; and
• $t'$ — Time in the fast-moving reference frame.

Now that we almost know what to expect from an object moving close to the speed of light (at relativistic speeds), we can introduce the barn-pole paradox.

Let's introduce our paradox. Take a barn with length $L$ and two doors on the opposite sides. Keep the doors open for the moment. Next up, take a pole (or a ladder, in other formulations of the paradox), accelerate it to relativistic speeds, and once it reaches a constant speed, shoot it straight in the direction of the barn's doors.

The pole has a length $l$, and we set the following condition:

That is, the pole won't fit in the barn in normal conditions. The pole moves at speed $v$. We can define the ratio of the speeds, $\beta$ as:

This is a useful indication of the speed of a relativistic object compared to the speed of light. From $\beta$ we calculate the Lorentz factor $\gamma$:

How does relativity affect this situation? Is it possible to contain the pole in the barn? We begin by analyzing the problem from the barn's point of view.

Imagine being a farmer observing the barn: you would agree with the following analysis as you would share the frame of reference with the barn. The pole darts in a fraction of a second in your field of view, zooming past the barn. What happened? Let's play a slo-mo on the barn!

The first thing we notice, as the pole approaches, is that it appears shorter: it underwent length contraction, and from our frame of reference, its length became:

You may get where we are going! Let's see what happens when the pole meets the barn.

Initially, the doors are both open. At the time $t_{\mathrm{i,f}}=0$, the front of the pole crosses the barn's front door. After a time $t_{\mathrm{i,b}}$, the back end of the pole crosses the same door. This time is given by:

Since we arbitrarily fixed $t_\mathrm{i,f}=0$, we can simplify this expression to:

The front end of the pole crosses the back door at the time $t_{\mathrm{o,f}}$ given by:

We simplified the formula again. The last time we can define is the time at which the back end of the pole exits the barn, thus completing the passage. To calculate it, we use the following formula:

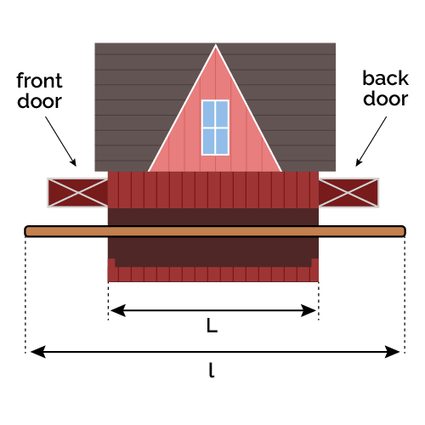
However, we are interested in the times $t_\mathrm{i,b}$ and $t_\mathrm{o,f}$: if the entrance time of the back comes before the exit time of the front end, for the time $t_\mathrm{o,f} - t_\mathrm{i,b}$ the contracted pole is entirely contained by the barn: we can close both doors simultaneously at a time $t_\mathrm{d} = (t_\mathrm{o,f} - t_\mathrm{i,b})/2$, and reopen them instantaneously without the pole touching any of them! In the graphics below, you can see the various steps of this passage:

If you accept the weirdness of length contraction, this scenario is not hard to understand. Let's give it some numbers. Take a pole with length $l=12\ \mathrm{m}$ crossing a small barn with length $L=6\ \mathrm{m}$ (let's say you are aiming for the broad side of the barn). The pole is traveling at $90\%$ of the speed of light, hence we can write $v = 0.9c$, with $\beta = 0.9$, and consequently, we find the Lorentz factor $\gamma$:

This speed causes our pole to contract to a length $l_\mathrm{conc}$ given by:

Yup: it looks like it will fit! Set the entry time of the front end of the pole at $t_\mathrm{i,f} = 0\ \mathrm{ns}$.

The back end of the pole enters the barn at the time $t_\mathrm{i,b}$:

The front end of the pole crosses the barn, reaching the back door at the time:

Thus, between the time $t_\mathrm{i,b} = 19.386\ \mathrm{ns}$ and the time $t_\mathrm{o,f} =22.238\ \mathrm{ns}$ we can "comfortably"" close both barn's doors simultaneously, trapping the pole inside for a sec-nanosecond! The time at which the doors close is:

Things, however, are relative!

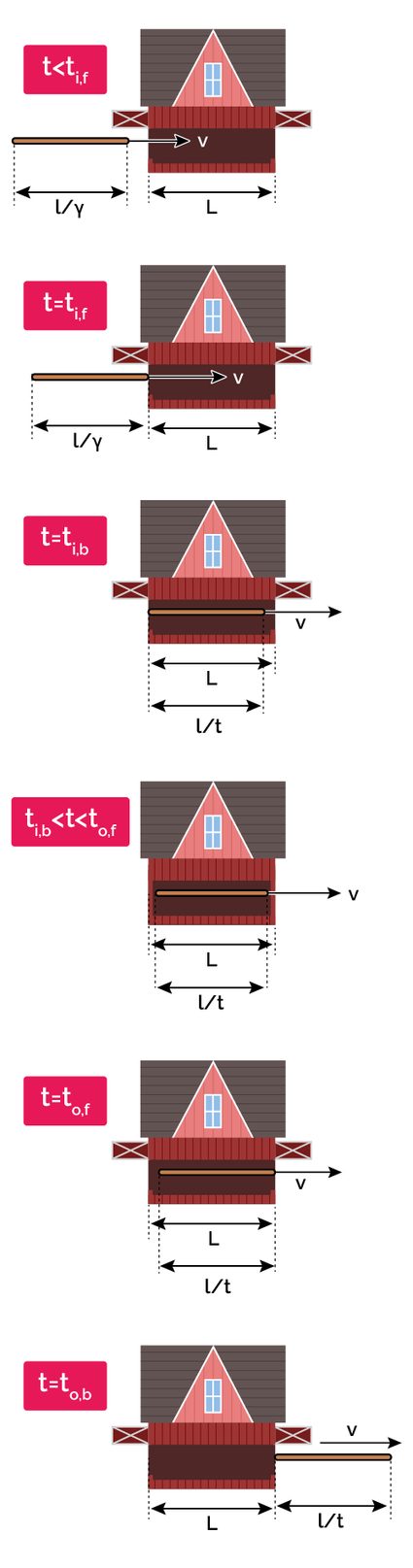
Let's now move to the pole's frame of reference. As the pole is not accelerating (it moves at constant speed), this is an inertial frame of a reference, which means that from the pole's point of view, the pole can be as well stationary, while the Universe around it moves at a constant speed matching its own. The diagram below shows what's going on:

In this frame of reference, it looks like the barn is rushing toward us at relativistic speed: it then experiences a length contraction! The new length of the barn is:

The barn is even shorter than before: the pole will never fit... or will it? Let's discover it! In this first analysis, imagine keeping the doors open to clock the pole crossings. The barn's front door meets the front end of the pole at $t'_\mathrm{i,f}$. We can set this value to zero for convenience. Let's move to the next step: in this case, the pole's front end exiting the barn's back door:

What comes after is the entrance and exit of the back end of the pole. For the crossing of the front door, we have:

That is the time needed to cover the length of the non-contracted pole at speed $v$. The exit happens after the length of the contracted barns crosses the back end of the pole:

Somewhere between these events, the doors of the barn close. These two events are simultaneous in the barn frame of reference; however, they happen in two different positions in space. Thus, we can apply the Lorentz's transformation. We use them at the time of the opening of the doors calculated in the barn's frame of reference, and the coordinates $x_\mathrm{f} = 0$ and $x_\mathrm{b} = L$. Let's find the time at which each door closes:

Notice that in this case, this expression simplifies to $t'_\mathrm{f} = \gamma\cdot t_\mathrm{d}$.

The back door closes at:

These two times differ! The closing of the doors is not simultaneous in the frame of reference of the pole!

We will soon understand this concept better, but first, let's find some concrete values for this frame of reference, too! Let's start with the same parameters we used in the barn's frame of reference: $l=12\ \mathrm{m}$, $L=6\ \mathrm{m}$, and $v=0.9c$. In the pole's frame of reference, the barn's length changes to:

As said previously, we fix the entrance time of the front end of the pole at $t'_\mathrm{i,f} = 0\ \mathrm{ns}$. The front end of the pole exits the barn at the time $t_\mathrm{0,f}$, given by:

The back end of the poles enters the barn at the time:

The exit time of the pole's back end is:

You can see that the two ends are never simultaneously inside the barn. Let's see when the doors close! The front door closes at the time:

The back door closes at the time:

We can reorder these events: the back door closes (and reopens), trapping the pole's front end. However, the front end leaves before the pole's back end can even enter the barn! The front door closes and opens much after the front leaves.

Let's recap the barn-pole paradox: from the barn's point of view, a contracted relativistic pole (longer than the barn, at rest) rushes and, for a fraction of a second, fits inside the barn in such a way that we can close and reopen the doors at the same moment. In the pole's frame of reference, the barn contracts! The already too-long pole will never fit in the barn. However, as the pole moves at a relativistic speed, its relative space-time will differ. In particular, the concept of simultaneity will change!

In the barn's frame of reference, the doors open and close simultaneously. However, from the pole's point of view, these two events happen at different times. Remember to imagine the barn rushing toward the pole: it will make much more sense. The back door closes when the front of the pole is contained in the barn and proceeds to open again to let it get out. After a given time, the back of the pole enters the barn, and the front door closes and reopens behind it. As these events are not simultaneous, the pole is not entirely contained in the barn at a specific time.

A Minkovski space-time diagram helps visualize the barn-pole paradox's solution. In the image below, you can see the diagram: in pink, we see the space-time occupied by the barn, and in blue, the path of the pole. In the upper right corner, we depicted the axes: the orthogonal ones are the ones of the barn's frame of reference. The relativistic speed of the pole causes its axes to "tilt".

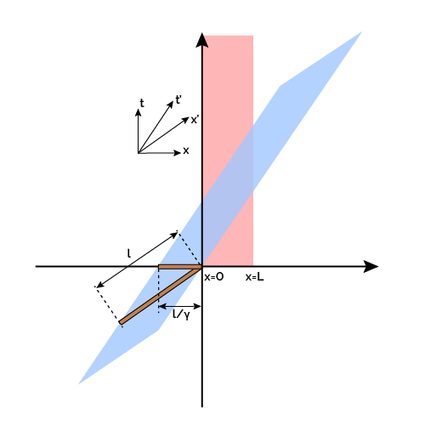
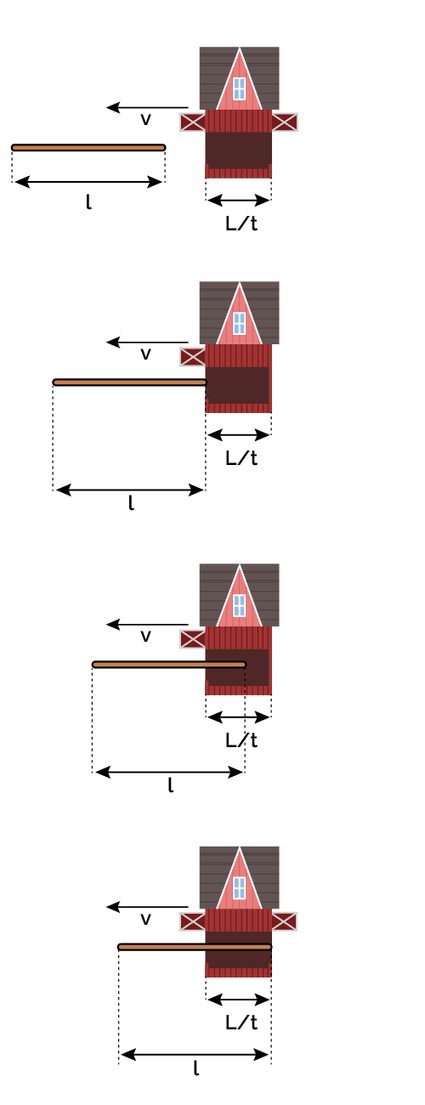
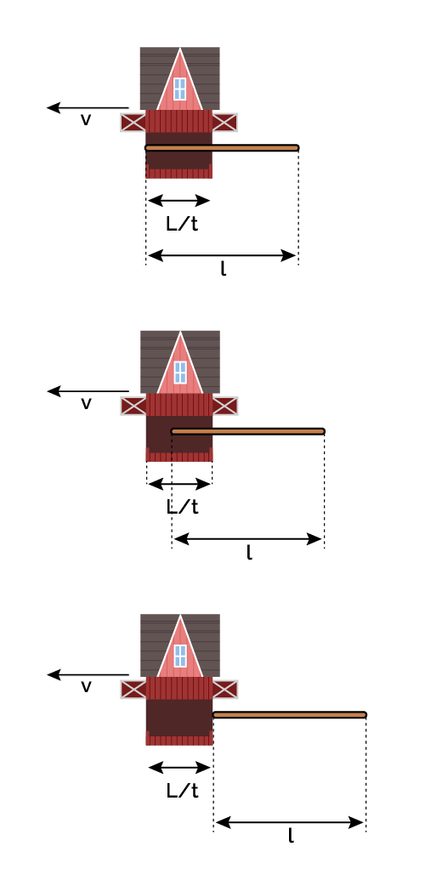
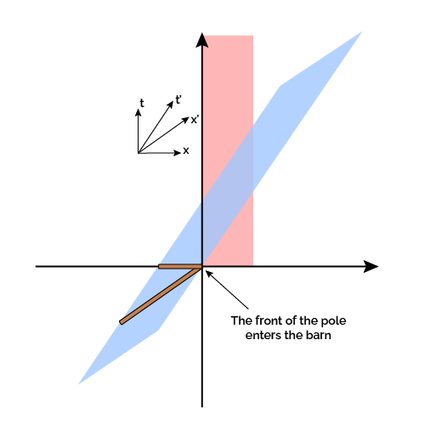
In the six images below, we depicted our thought experiment's crucial moments. The pole enters the barn at the same time in both frames of reference. The following snapshot happens when the back of the pole enters the barn in the barn's frame of reference. You can see how, from the pole's point of view, this event still has to happen! Right after this, the doors close simultaneously in the barn's frame of reference.

Notice that this event happens much later in the subjective time of the pole, as its time is dilated. In the fourth snapshot, the front of the pole exits the barn. This is all from the barn's point of view; the rest of the pole follows suit. However, in the pole's frame of reference, there is still much going on! After a while, the pole's back enters the barn! The front door finally closes and opens behind it, trapping the back end (only the back end!).

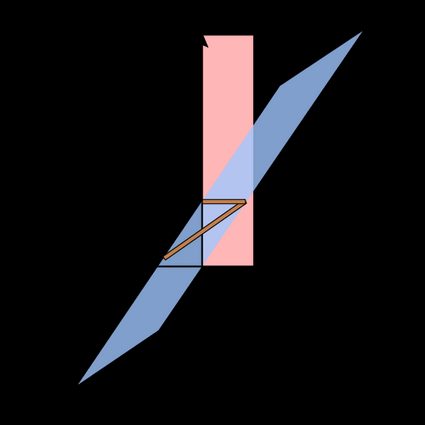
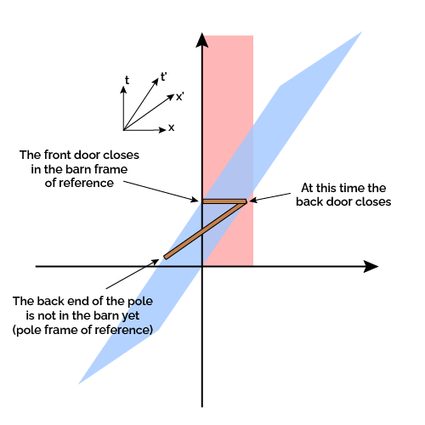
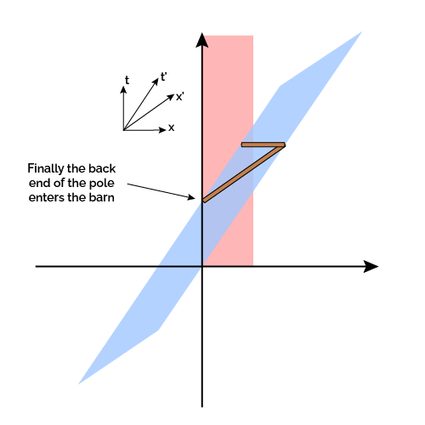
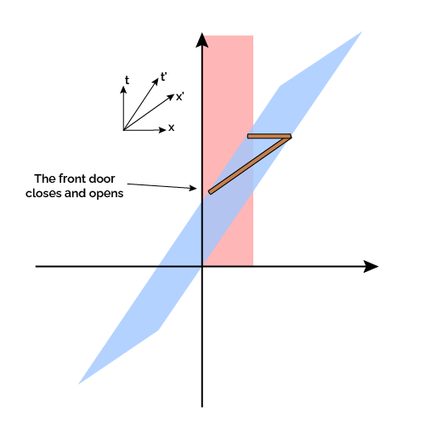
From these diagrams, it is clearly visible that the opening of the doors is not a simultaneous event in the pole's frame of reference. The paradox is solved by removing the constraint of simultaneousness, almost in the same way we removed the constraint of rigidity in the bug rivet paradox.

Traveling in space at high speed opens a whole world of complications: luckily, we still have a long way to go and plenty of time to figure out how to deal with relativity!