Last updated: Dec 09, 2024

Frequency Bandwidth Calculator

Q: How is bandwidth related to frequency?

The frequency bandwidth is defined as the difference between the upper and the lower cutoff frequencies, as we see in the equation below: f BW = f u - f l Or you can find it by taking the ratio between the center frequency and the quality factor: f BW = f 0 /Q You can compute it easily using our frequency bandwidth calculator .

Q: What frequency band is 5G?

The 5G communication network works with three different sets of frequency bands. These sets may vary by region and are called low-band (600 MHz to 1 GHz), mid-band (1 GHz to 6 GHz), and high-band (24 GHz to 40 GHz).

Q: What is the radio frequency bandwidth?

FM radio stations usually operate in a frequency range between 80 MHz and 110 MHz , so they require a frequency bandwidth of around 0.2 MHz . There are also AM radio stations , which typically cover a frequency range between 500 KHz and 1700 KHz and require a frequency bandwidth of 10 KHz .

Q: What is the quality factor for a center frequency of 1420 MHz?

If we consider a center frequency of 1420 MHz and a frequency bandwidth of 1 MHz , the quality factor can be determined using the steps below: Take the center frequency f 0 = 1420 MHz ; Take the frequency bandwidth f BW = 1 MHz ; Substitute these values in the equation below to find the quality factor: Q = f 0 / f BW = 1420 This is the quality factor used to measure the local hydrogen emitted by the center of the Milky Way .

Created by João Rafael Lucio dos Santos, PhD

João Rafael Lucio dos Santos

PhD, Federal University of Campina Grande

LinkedInWebsiteResearch Gate

Joao is a physicist, researcher, and professor in Brazil. He earned his Ph.D. in Physics at the University of Rochester, NY in 2013. He has written several papers in international journals, mainly in field theory and cosmology. Joao is also a researcher and the outreach leader for the BINGO telescope. This state-of-the-art radio telescope will be operating in the Northeast of Brazil in a few years. He believes in the importance of spreading knowledge and high-quality information among society and the public in general. He also believes that people can enjoy the learning process if it is funny and if they can see it as a path to change their life, even in daily activities. In his free time, he enjoys running, playing tennis, cooking, traveling, and having pleasant moments with his relatives and friends. See full profile

Check our editorial policy

Reviewed by Steven Wooding

Steven Wooding

Physicist holding a 1st class degree and a member of the Institute of Physics. Creator of the UK vaccine queue calculator, and featured in many publications, including The Sun, Daily Mail, Express, and Independent. Tenacious in researching answers to questions and has an affection for coding. Hobbies include cycling, walking, and birdwatching. You can find him on Twitter @OmniSteve. See full profile

Check our editorial policy

New

Table of contents

What is frequency bandwidth?How can I determine the frequency bandwidth? Center frequency and quality factor How to use the frequency bandwidth calculator Finding the frequency bandwidth — an example FAQs

If you are looking for the frequency bandwidth for a given center frequency and a specific quality factor, we have the perfect tool for you: the frequency bandwidth calculator. Along with this article, we are going to answer questions such as:

What is frequency bandwidth?
What are the upper and the lower cutoff frequencies?
What are the center frequency, the resonance frequency, and the quality factor?
How is bandwidth related to frequency?
What frequency band is 5G?
What is the radio frequency bandwidth?

Let us help you to characterize your radio signal using our frequency bandwidth calculator.

What is frequency bandwidth?

The frequency bandwidth is the difference between the upper and lower frequencies in a continuous band of frequencies that a system can have or process.

Bandwidth is an essential concept for signal transmission, as it can change data rates, quality, and resolution. It can be applied in several scenarios, such as satellite and space communications, Wi-Fi and wireless networks, radio, sonar, and radar signals, medical imaging, etc.

It seems complicated for someone who has never studied a frequency spectrum graphic. However, we are going to show you how simple the definition is and how you can compute the frequency bandwidth easily and instantaneously.

How can I determine the frequency bandwidth? Center frequency and quality factor

We can calculate the frequency bandwidth using two values: the center frequency and the quality factor. The formula to compute it is given by:

f_{\rm BW} = \frac{f_0}{Q}

where:

$f_{\rm BW}$ — Frequency bandwidth;
$f_0$ — Center frequency (also known as the resonance frequency); and
$Q$ — Quality factor.

In the previous formula, the quality factor represents how underdamped an oscillator or resonator is. In other words, it informs you how well a system can resonate by taking a specific frequency.

The center frequency measures the frequency between the upper and the lower cutoff frequencies for a given bandwidth. In signal transmission/reception, the center frequency is the reference where a filter, a channel, or a signal is focused. Such a frequency is also known as geometric center frequency or geometric mean, whose equation is:

f_0 = \sqrt{f_u \cdot f_l}

where

$f_u$ — Upper cutoff frequency; and
$f_l$ — Lower cutoff frequency.

The cutoff frequencies allow us to define the frequency bandwidth as

f_{\rm BW} = f_u - f_l

In the frequency spectrum graphic below, we show how to define the frequency bandwidth by setting the upper and the lower cutoff frequencies.

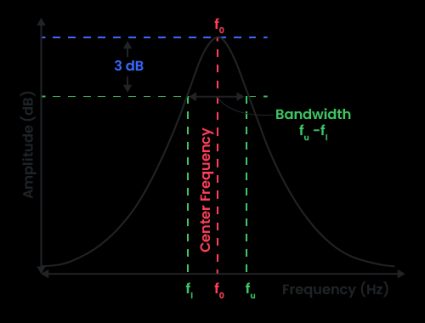
Frequency spectrum graphic showing the parameters that define the frequency bandwidth.

🙋 You can learn more about cutoff frequencies by checking our cutoff frequency calculator.

This difference between the upper and the lower cutoff frequencies is also known as 3 dB or half-power point. This specific point corresponds to a difference of half power between the center frequency and the cutoff frequencies. The 3 dB defines the frequency range where the system maintains its effective signal transmission/reception. To understand how a 3 dB difference corresponds to half power attenuation, let us consider the definition of power:

P (\mathrm{dB}) = 10 \times \log_{10}\left(\frac{P_{\rm CO}}{P_{\rm Cf}}\right)

where:

$P$ — Power in dB;
$P_{\rm CO}$ — Power at the cutoff frequency; and
$P_{\rm Cf}$ — Power at the center frequency.

Then, by setting $P = - 3 \, \mathrm{dB}$ in the previous equation we find:

\footnotesize \begin{split} & -0.3 = \log_{10}\left(\frac{P_{\rm CO}}{P_{\rm Cf}}\right) \\[0.8em] & \frac{P_{\rm CO}}{P_{\rm Cf}} = 10^{-0.3} \approx 0.5 \end{split}

You can learn more about frequency, power, and antennas by accessing our EIRP calculator.

Moreover, the upper and lower frequencies can be determined from the quality factor and the center frequency using the equations below:

\footnotesize \begin{split} & f_u = f_0\,\left(\sqrt{1+\frac{1}{4 Q^2}}+\frac{1}{2Q}\right) \\[1.2em] & f_l = f_0\,\left(\sqrt{1+\frac{1}{4 Q^2}}-\frac{1}{2Q}\right) \end{split}

If you want to learn how the previous formulas were derived, take a look at the concepts about RLC circuits in the sources of this article, and also do not forget to check our RLC circuit calculator.

We know it is a lot of information, but you do not need to worry. Our frequency bandwidth calculator is here to make the hard work for you as fast as a radio signal traveling.

How to use the frequency bandwidth calculator

Here, we will show you how simple and easy using our frequency bandwidth calculator is. In the data section of our calculator, you just need to provide the center frequency and the quality factor. Then, it will instantaneously determine the frequency bandwidth, the upper cutoff frequency, and the lower cutoff frequency.

Our Omni Calculator tools are always designed to work back and forth. So, you can, for instance, insert your upper and lower cutoff frequencies to determine the quality factor, the frequency bandwidth, and the center frequency. We invite you to explore our frequency bandwidth calculator and verify how it can be useful for you.

Finding the frequency bandwidth — an example

Suppose you want to listen to your favorite radio station with a center frequency of 93.7 MHz and a quality factor of 500. What are the upper and the lower cutoff frequencies, and what is the frequency bandwidth in the frequency spectrum? To answer this question, we can first apply the data to the frequency bandwidth equation:

\footnotesize f_{\rm BW} = \frac{93.7 \times 10^{6}}{500} = 0.1874 \, \mathrm{MHz}

Moreover, by using the definition of the lower and upper cutoff frequencies in terms of the center frequency and of the quality factor, we obtain:

\footnotesize \begin{split} f_l &= \left(\sqrt{1+\frac{1}{4\times 500^2}}-\frac{1}{10^{3}}\right) \\[0.8em] &\qquad \times 93.7 \times 10^{6} \\[0.8em] f_l &= 93.6 \, \mathrm{MHz} \end{split}

\footnotesize \begin{split} f_u &= \left(\sqrt{1+\frac{1}{4 \times 500^2}}+\frac{1}{10^{3}}\right) \\[0.8em] &\qquad \times 93.7 \times 10^{6} \\[0.8em] f_u &= 93.8 \, \mathrm{MHz} \end{split}

Or you can skip all these calculations and discover the answer in a second with our frequency bandwidth calculator.

FAQs

How is bandwidth related to frequency?

The frequency bandwidth is defined as the difference between the upper and the lower cutoff frequencies, as we see in the equation below:

f_BW = f_u - f_l

Or you can find it by taking the ratio between the center frequency and the quality factor:

f_BW = f₀/Q

You can compute it easily using our frequency bandwidth calculator.

What frequency band is 5G?

The 5G communication network works with three different sets of frequency bands. These sets may vary by region and are called low-band (600 MHz to 1 GHz), mid-band (1 GHz to 6 GHz), and high-band (24 GHz to 40 GHz).

What is the radio frequency bandwidth?

FM radio stations usually operate in a frequency range between 80 MHz and 110 MHz, so they require a frequency bandwidth of around 0.2 MHz. There are also AM radio stations, which typically cover a frequency range between 500 KHz and 1700 KHz and require a frequency bandwidth of 10 KHz.

What is the quality factor for a center frequency of 1420 MHz?

If we consider a center frequency of 1420 MHz and a frequency bandwidth of 1 MHz, the quality factor can be determined using the steps below:

Take the center frequency f ₀ = 1420 MHz;
Take the frequency bandwidth f_BW = 1 MHz;
Substitute these values in the equation below to find the quality factor:

Q = f ₀/ f_BW = 1420

This is the quality factor used to measure the local hydrogen emitted by the center of the Milky Way.