Sunset Calculator

Our sunset calculator will surprise you with the simple math behind the calculations for the sunset time. Discover the numbers behind the most romantic moment of the day with Omni Calculator.

You will learn, among other things:

• What's sunset and the various types of the sunset?
• How to calculate the sunset time if there was no atmosphere.
• The refraction correction.

And much more!

Sunset is the moment of the day when the Sun dips below the horizon in the evening. The sunset, or sundown marks the beginning of the night: the last lights of the day inspired generations of artists in their creations and fascinate people literally around the world every day. Everyone stared in admiration at a mesmerizing sunset with thousand shades of red, pinks, and oranges at least once.

The fact that the sunset is accompanied by a plethora of other events, from the elusive green flash to the Earth's shadow in the atmosphere, contributed to the attractiveness of this phenomenon. However, from an astronomical point of view, it's not special at all!

Sunset is the most desired moment of the day for astronomers, who can finally whip out their instruments to start their nightly exploration of the skies. Or can they?

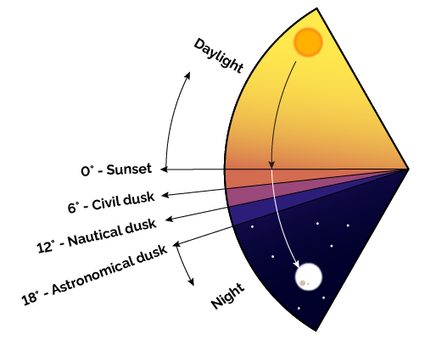
While sunset is the moment of the day when the Sun is crossing the horizon (we say it is $0\degree$ above it), it doesn't mark the beginning of the darkness. The light merely dims! In fact, the sunset, as we commonly intend it, marks the beginning of the twilight, which terminates when the Sun reaches $6\degree$ below the horizon. At this time, you may start spotting some particularly bright stars (Vega, Betelgeuse, or Canopus) and some planets (even though Venus may appear even in the daylight!). Usually, you can walk around without needing artificial lighting.

When you finally need to turn on a flashlight to see around you, you enter the nautical twilight. This sunset phase lasts until the Sun reaches $12\degree$ below the horizon, and astronomers define it as the phase in which you can still discern the horizon. After the nautical twilight, all stars that you can see with the naked eye are there for your amazement.

Still, you must wait until the astronomical twilight, when the Sun finally crosses $18\degree$ below the horizon, to see the faint nebulas and clusters that decorate the night sky. Let's Sun... sum them up!

• Sunset – $0\degree$ (on the horizon);
• Civil twilight – $0\degree$ and $6\degree$ below the horizon;
• Nautical twilight – $6\degree$ and $12\degree$ below the horizon;
• Astronomical twilight – $12\degree$ and $18\degree$ below the horizon; and
• Night – Below $18\degree$.

In the following sections, we will teach you how to use the formula to calculate the sunset time: you will be surprised by how little data are required and how simple are the equations we need!

Let's first understand the nature of our problem. When we calculate the sunset hours, we are looking for the hours at which the Sun makes contact, and crosses, the horizon. We need to introduce some quantities related to these calculations, but first, let's analyze the problem!

The Earth orbits around the Sun on a plane we project on the sky as the ecliptic. The ecliptic and Earth's equator lie at an angle of $23.45\degree$, and remain in a fixed position relative to each other.

This tilt relative to Earth's orbital plan allows one hemisphere to receive more sunlight during half of the year and lie in relative darkness during the other half, depending on the direction in which Earth's axis points. During winter, for the northern hemisphere, the north side of the axis points outside the orbit. The effect is that in the winter, the height reached by the Sun in the northern hemisphere is lower than in the summer. You can understand this concept better by using pictures!

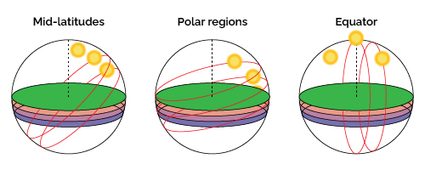
Remember that the angle remains unchanged: from our Earthly perspective, we see the Sun changing position as illustrated in the figure above for a generic location in the northern hemisphere.

What changes during the year is the Sun declination, the angle between solar rays — which reach Earth as parallel lines — and the equatorial plan. This angle varies from $+24.45\degree$ to $-23.45\degree$, reaching the maximum values in the solstices. During the equinoxes (in spring and autumn), the declination is $0\degree$, and Earth's equator coincides with the ecliptic.

Calculating the declination is the first step to finding the sunset hour. To do so, we choose a point on Earth, defined by the coordinates $\phi$ and $\lambda$, respectively latitude and longitude.

After fixing the space, we need to set the time: choose the day for which you want to calculate the sunset. We can't input a date in the algorithm, so we will calculate the day number, starting from $1$ for the first of January. Call this number $n$.

Our first formula to calculate the sunset allows us to find the approximate time of the phenomenon in days, starting from the first of January at midnight:

After all, six in the afternoon is not a bad moment for the sun to set. In the formula, $\lambda_{\mathrm{hour}}$ is a measure of the longitude in hours: we find it with the simple formula:

since $360/24=15$.

Next step: considering the characteristic of Earth's orbit. We will calculate the Sun's mean anomaly, which measures the deviation of an elliptic orbit from a circular one.

We measure this quantity in degrees. It corresponds to how much the Earth overshot the trajectory on the imaginary circular orbit with the same orbital period as the actual elliptic one.

The following two passages will use this quantity to find a reasonable estimate of the Sun's coordinates in the sky: did you know that stars and planets have coordinates as any place on Earth? Obviously, their position depends on the point of view: such a system is strictly geocentric, but it works wonders! This is why we calculate the Sun's true latitude and right ascension (the analog to the longitude).

For the true latitude, we use the following formula:

And for the right ascensions this one:

Both these quantities must fall in the same quadrant of the sky: while the true latitude is easy to fix (we use the equator as a reference), the right ascension, as the latitude, needs an arbitrary reference. To fix this uncertainty, calculate these two values:

And update the value of the right ascension according to the following:

Now convert this last result in hours by dividing it by $15$ as we did for the latitude:

We have all the ingredients to find the time of sunset. Let's calculate the Sun declination first:

This quantity is enough to calculate the local hour angle. The hour angle, in general, is the moment of the day in which the Sun reaches a specific position: we marked it with the variable $z$ degrees, and it corresponds to the degrees after the vertical over your head, the zenith.

For the sunset, you have a bit of choice when it comes to $z$:

• For the sunset (when the Sun's center crosses the horizon), set $z=90\degree$;
• For the civil twilight set $z = 96\degree$;
• For the nautical twilight set $z = 102\degree$; and
• For the astronomical twilight set $z = 108\degree$.

Once done, we can calculate the local mean time of the sunset in UTC:

Now we need to correct this result according to three factors:

• Longitude of the desired place;
• Local time zone; and
• Eventual use of daylight savings (if applicable).

where:

• $\lambda_{\mathrm{h}}$ — Longitude expressed in hours;
• $\mathrm{tz}$ — Local time zone; and
• $\mathrm{ds}$ — Correction due to daylight saving time: if the desired location is currently using that time, assign value $1$ to $\mathrm{dz}$, otherwise, leave it at $0$.

If you use our sunset calculator, you will notice that the results under the section uncorrected are incorrect. We meant "uncorrected" in a scientific way, as in "without correction". 😛

Anyway, the reason for the discrepancy between the real sunset time and the one we calculated with the formulas above is atmospheric refraction. Earth's atmosphere changes with height, as you can observe by climbing a tall mountain: the higher you go, the lower the pressure and, simultaneously, the density. This change in density is responsible for a continuous variation of the atmosphere's refraction index: as a consequence, the Sun's light rays bend: you can clearly picture this phenomenon:

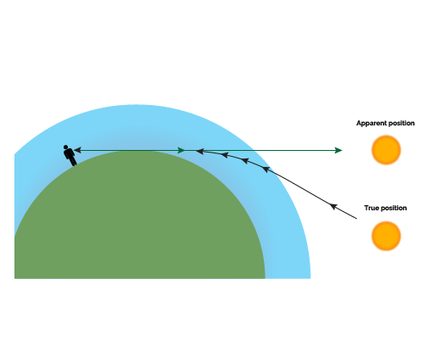
This effect peaks in intensity at sunrise and sunset, where the total deviation amounts to $0.58\degree$. It may not sound like a lot, but it gives you six minutes of sunlight more for each side!

How do we model the atmospheric refraction in our formulas to calculate the sunset time? We change the zenith angle to $90.833\degree$. This way, we include both the effect of refraction and the Sun's diameter (defining sunset as the time the last portion of the Sun's disk disappears below the horizon). The new hour angle is, as a result of this, defined as:

This is the most accurate modeling we can offer you when calculating the sunset time. Notice that we didn't include the effect of refraction in the other types of dusk: the higher the angle, the lower the effect, and for such "weakly" defined phenomena, the difference would be, at most, arbitrary.

Why stop at sunset? The formulas you met in our sunset calculator work for the sunrise, too: visit Omni's sunrise and sunset calculator or the more specific tools:

• The sunrise calculator; and
• The daylight calculator.

There's no simple equation to calculate the sunset. Here are, indicatively, the steps to find the sunset time:

1. Calculate the position of the Sun on the projection of Earth (true latitude and longitude).

2. Calculate the position of the Sun in the sky (declination and right ascension).

3. Find the hour angle of the desired phenomenon.

4. Calculate the sunset time in UTC, knowing the angular speed of the Sun.

5. Convert UTC to local time with the addition of longitude, timezone, and, eventually, daylight savings adjustments.

We can identify four types of sunsets, variations of the same phenomenon:

• The proper sunset (or dusk);
• The civilian dusk, when the Sun crosses the line 6 degrees below the horizon;
• The nautical dusk, when the Sun reaches 12 degrees below the horizon; and
• The astronomical dusk that marks the beginning of the last influences of sunlight in the night sky.

Refraction causes the Sun's rays to bend when crossing the various layers of the atmosphere. We can easily calculate the effects of atmospheric refraction in our formulas for the sunset by changing the definition of "when" the Sun sets, adding 0.833 degrees to the angle we use to define the moment of the sunset.

To calculate the sunset from the hour angle, follow these easy steps:

1. Calculate the hour angle for the desired phenomenon. In our case, the sunset, or when the angle from the zenith is 90°.

2. Use the hour angle to calculate the UTC time of the local sunset.

3. Adjust the result of the calculations to account for the local language, timezone, and the eventual presence of daylight savings.