Kalkulator gwintów

Nasz kalkulator gwintów pomoże ci znaleźć różne wymiary gwintów nakrętek i śrub zgodnie z normami metrycznymi ISO. Z tego kalkulatora gwintów dowiesz się:

• Jak określić rozmiary gwintów metrycznych;
• Jak czytać i rozumieć specyfikację gwintów;
• Jakie są wzory na wymiary gwintów zewnętrznych;
• Jakie są wzory na wymiary gwintów wewnętrznych; oraz
• Co oznacza klasa gwintu metrycznego.

Zacznijmy od dowiedzenia się, czym są gwinty. 🔩

Gwint śruby wykonany z rowków i grzbietów owiniętych wokół cylindrycznego lub stożkowego metalowego wału w układzie spiralnym. Spiralny wzór gwintu działa jak pochylona płaszczyzna, która przekłada ruch obrotowy na ruch osiowy, jednocześnie zyskując pewną mechaniczną przewagę.

W rezultacie gwint śruby pełni także funkcję blokującą, która wymagałaby dużej ilości naprężeń ścinających do zerwania, co czyni go doskonałym do łączenia przedmiotów. Ten rodzaj gwintu może być gwintem zewnętrznym (jak na śrubie lub wkręcie) lub gwintem wewnętrznym (jak to, co widzimy wewnątrz nakrętki).

Choć gwinty występują również w innych zastosowaniach, takich jak zakrętki do butelek, żarówki, rury i złącza, a nawet przekładnie ślimakowe, ten kalkulator gwintów skupia się w szczególności na gwincie metrycznym. Gwinty metryczne mają symetryczne gwinty w kształcie litery V, które tworzą rowki pod kątem 60º i mają podstawowe wymiary pokazane poniżej:

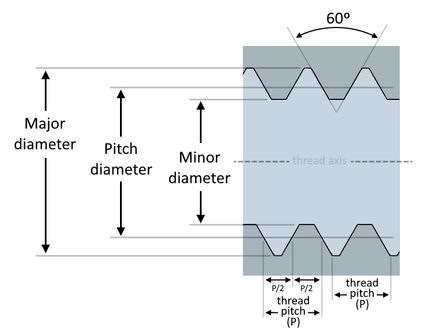
Średnica zewnętrzna to największa średnica gwintu. Nazywamy ją również średnicą brutto lub średnicą nominalną gwintu. Z drugiej strony, średnica wewnętrzna jest najmniejszą średnicą gwintu. Nazywamy ją również średnicą podstawową lub rdzeniową gwintu.

Pomiędzy tymi dwiema średnicami znajduje się średnica podziałowa. Średnica podziałowa to średnica gwintu, w której grubość gwintu i przestrzeń między dwoma gwintami są równe. Możemy przybliżyć wartość średnicy podziałowej, biorąc średnią z mniejszej i większej średnicy gwintu. Odwiedź nasz kalkulator średnicy podziałowej 🇺🇸, aby dowiedzieć się więcej na ten temat.

Skok gwintu lub po prostu skok to odległość między punktem na jednym gwincie a odpowiadającym mu punktem na gwincie sąsiadującym z nim (na przykład, pomiar od wierzchołka do wierzchołka lub od nasady do nasady). Dowiedz się więcej o skoku gwintu, sprawdzając nasz kalkulator skoku gwintu 🇺🇸.

Zrozumienie gwintów metrycznych zaczyna się od umiejętności czytania oznaczeń gwintów metrycznych. Oznaczenie gwintu jest takie samo jak etykieta gwintowanego elementu złącznego, gdy widzisz je w sklepie z narzędziami. Każdy standard gwintu ma swoje własne objaśnienie gwintu, a oto przykład oznaczenia gwintu metrycznego:

$\text{M10 × 1 × 25}$

Odczytujemy to oznaczenie jako M-Dziesięć na jeden na dwadzieścia pięć", gdzie:

• $\text{M}$ oznacza metryczny i oznacza, że gwinty są zgodne z normą metryczną ISO;
• $10$ w tym przypadku liczba umieszczona przy literze M oznacza średnicę zewnętrzną gwintu;
• $1$ reprezentuje skok gwintu; oraz
• $25$ jest długością trzpienia.

Wszystkie wymiary w oznaczeniu gwintu metrycznego są podane w milimetrach.

Teraz gdy potrafimy już odczytywać oznaczenia gwintów metrycznych, możemy zacząć obliczać różne wymiary naszych gwintów. Znajomość sposobu określania rozmiarów gwintów metrycznych daje nam kolejny sposób na odróżnienie jednego gwintu od drugiego. Jako przewodnika użyjemy poniższej ilustracji:

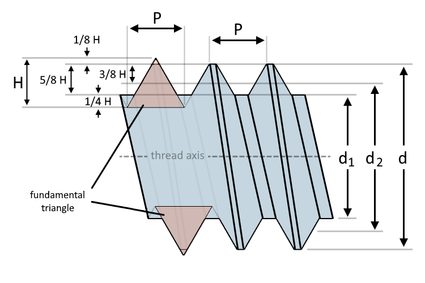
Na powyższej ilustracji widzimy, że możemy użyć ułamków H do określenia różnych wymiarów gwintu metrycznego, biorąc pod uwagę średnicę zewnętrzną ($\small{d}$). Ale czym jest H? $\small{H}$ jest wysokością trójkąta podstawowego gwintu. Trójkąt podstawowy to rzutowany trójkąt równoboczny, który możemy utworzyć z przekroju poprzecznego gwintu. Jego wysokość możemy obliczyć za pomocą poniższego wzoru:

gdzie:

• $P$ — skok gwintu.

Analizując powyższy schemat, możemy następnie sformułować następujące równania, aby znaleźć inne podstawowe średnice gwintu zewnętrznego:

• $d_1 = d - 2 \cdot \frac{5}{8} \cdot H$

• $d_2 = d - 2 \cdot \frac{3}{8} \cdot H$

gdzie:

• $d$ — Średnica zewnętrzna;
• $H$ — Wysokość podstawowego trójkąta;
• $d_1$ — Średnica wewnętrzna gwintu; oraz
• $d_2$ — Średnica podziałowa gwintu.

Zasadą jest, że gwint wewnętrzny o danym rozmiarze powinien mieć taką samą średnicą zewnętrzną jak gwint zewnętrzny o tym samym rozmiarze. Oznacza to, że $d_1 = D_1$, i $d_2 = D_2$ gdzie $D_1$ i $D_2$ są odpowiednio średnicą wewnętrzną i średnicą podziałową gwintu wewnętrznego.

Na podstawie tego, co już omówiliśmy, średnice pary gwintów zewnętrznych i wewnętrznych dokładnie do siebie pasują. Jednak w większości przypadków występuje pewna tolerancja dla naszych gwintów, aby mieć swobodę podczas dopasowywania ich do siebie. W tym miejscu do gry wkraczają klasy gwintów metrycznych.

Klasy gwintów metrycznych wskazują stopień tolerancji i klasę gwintu metrycznego. Każda klasa tolerancji ma odpowiednie równania, które informują nas, o ile głębiej powinniśmy naciąć lub walcować gwinty na zimno, aby uzyskać pożądane parametry.

Istnieją jednak ograniczenia co do tego, jak bardzo możemy odejść od podstawowych wymiarów gwintu. Dlatego dobrze jest znać dopuszczalne maksymalne i minimalne średnice naszych gwintów.

Oto wzory, których używamy do znalezienia tych maksymalnych i minimalnych średnic:

Dla średnicy zewnętrznej gwintu zewnętrznego(d):

• $d_\text{max} = d + es$
• $d_\text{min} = d + es - T_\text{d}$

Dla średnicy wewnętrznej gwintu zewnętrznego (d₁):

• $d_\text{1max} = d_1 - es - 2 \cdot y$
• $d_\text{1min} = d_1 - es - 2 \cdot z$

Dla średnicy podziałowej gwintu zewnętrznego (d₂):

• $d_\text{2max} = d_2 + es$
• $d_\text{2min} = d_2 + es - T_\text{d2}$

Dla średnicy zewnętrznej gwintu wewnętrznego (D):

• $D_\text{min} = D + EI$

Dla średnicy wewnętrznej gwintu wewnętrznego (D₁):

• $D_\text{1min} = D_1 + EI$
• $D_\text{1max} = D_1 + EI + T_\text{D1}$

Dla średnicy podziałowej gwintu wewnętrznego (D₂):

• $D_\text{2min} = D_2 + EI$
• $D_\text{2max} = D_2 + EI + T_\text{D2}$

gdzie:

• $es$ i $EI$ — odchyłki podstawowe, odpowiednio górna i dolna odchyłka;
• $T$ — Tolerancje dla odpowiadających im średnic (tj. $T_\text{d2}$ jest tolerancją średnicy skoku gwintu zewnętrznego ($d_2$)); oraz
• $y$ oraz $z$ — Wartości korekty odpowiednio dla maksymalnej średnicy mniejszej i minimalnej średnicy mniejszej.

Oto równania, których używamy do znalezienia tolerancji w zależności od tego, w jakiej klasieznajdują się gwinty:

Tolerancja (klasy) dla gwintów zewnętrznych

• Klasa e: $\small{es = -(50 + 11 \cdot P) / 1000}$;
• Klasa f: $\small{es = -(30 + 11 \cdot P) / 1000}$;
• Klasa g: $\small{es = -(15 + 11 \cdot P) / 1000}$; oraz
• Klasa h: $\small{es = 0}$.

Tolerancja dla gwintów wewnętrznych

• Klasa G: $\small{EI = (15 + 11 \cdot P) / 1000}$; i
• Klasa H: $\small{EI = 0}$.

Z drugiej strony, oto różne ogólne równania, których używamy do określania tolerancji w oparciu o klasę tolerancji gwintu:

!Dla gwintów zewnętrznych !

• $\small{T_\text{d}(n) = k \cdot (180 \cdot P^{2/3} - 3,15 \cdot P^{-1/2}) / 1000}$; oraz
• $\small{T_\text{d2}(n) = k \cdot (90 \cdot P^{0,4} \cdot d^{0,1}) / 1000}$

!Dla gwintów wewnętrznych !

• $\small{T_\text{D1}(n) = k \cdot (433 \cdot P - 190 \cdot P^{1,22}) / 1000}$ (dla 0,2 mm ≤ P ≤ 0,8 mm);
• $\small{T_\text{D1}(n) = k \cdot (230 \cdot P^{0,7}) / 1000}$ (dla P ≥ 1,0 mm);
• $\small{T_\text{D2}(n) = k \cdot (90 \cdot P^{0,4} \cdot d^{0,1}) / 1000}$

W tych równaniach wartość dla $k$ zależy od klasy tolerancji gwintu, oznaczonej przez $n$. Śruba z klasą tolerancji $n = 6$ dla jej głównej średnicy powinna używać $k = 1,0$ podczas rozwiązywania dla $T_\text{D1}$. Oto inne wartości k w poniższej tabeli:

W przypadku mniejszej średnicy możesz również zobaczyć, że mamy tam dwie inne zmienne regulacyjne, $y$ i $z$, włączone do równania. Poniżej znajdują się równania, których używamy do tego celu:

Wiemy, że $R_\text{min}$ jest równe $\frac{P}{8}$.

W przypadku gwintów z określonymi szczegółami klasy gwintu, możemy dodać ich kody na końcu nazwy gwintu. Na przykład, gwint zewnętrzny oznaczony jako $\text{M30 × 2 × 40 - 5g6g}$ oznacza, że ma klasę tolerancji średnicy podziałowej równą $5$ i klasę tolerancji średnicy zewnętrznej równą $6$, z których obie są zgodne z klasą $\text{g}$.

Zwykle wykonujemy tylko ręczne obliczenia, aby znaleźć podstawowe średnice gwintu. Jak być może zauważyłeś/aś, określenie limitów średnicy wymagałoby wielu dodatkowych kroków. I tu z pomocą przychodzi nasz kalkulator rozmiaru gwintu! Oto kroki, które musisz wykonać, aby skorzystać z naszego narzędzia:

1. Wybierz parametry, które chcesz obliczyć — metryczne wymiary gwintów zewnętrznych, wewnętrznych lub obu.
2. Wybierz skok gwintu z rozwijanego menu.
3. Wprowadź średnicę główną gwintu. Możesz pobrać ten wymiar z oznaczenia gwintu lub zmierzyć go za pomocą suwmiarki.
4. Wreszcie, w sekcji Szczegóły klasy tolerancji naszego kalkulatora gwintów metrycznych, wybierz klasę elementu złącznego, w zależności od tego, które z nich są ci znane. Możesz również zobaczyć te szczegóły na objaśnieniu gwintu metrycznego.

Po wykonaniu powyższych kroków natychmiast zobaczysz nie tylko podstawowe średnice, ale także najmniejszą i największą średnicę gwintu.

Możesz także kliknąć przycisk tryb zaawansowany (ang. advanced mode) poniżej naszego kalkulatora gwintów metrycznych, jeśli chcesz zapoznać się z różnymi wstępnymi pomiarami używanymi w obliczeniach, takimi jak wysokość podstawowego trójkąta, odchylenia, wartości tolerancji i korekty.

Załóżmy, że mamy śrubę o średnicy zewnętrznej (d) wynoszącej 10 mm i skok gwintu (P) wynoszący 1,5 mm. Aby znaleźć średnicę podziałową:

1. Najpierw oblicz wysokość jej podstawowego trójkąta (H) używając H = P ⋅ (√3) / 2. H = 1,5 mm ⋅ (√3) / 2 = 1,299 mm.
2. Następnie uzyskaj średnicę podziałową (d₂) przy użyciu d₂ = d - 2 ⋅ (3 / 8) ⋅ H, d₂ = 10 mm - 2 ⋅ (3 / 8) ⋅ 1,299 mm = 9,026 mm.

Załóżmy, że mamy śrubę o podstawowej średnicy głównej (d) 20 mm i skok gwintu (P) 2 mm. Aby znaleźć jej wewnętrzną średnicę:

1. Oblicz wysokość podstawowego trójkąta (H) używając H = P ⋅ (√3) / 2. H = 2 mm ⋅ (√3) / 2 = 1,732 mm.
2. Uzyskaj średnicę wewnętrzną (d₁), używając d₂ = d - 2 ⋅ (5 / 8) ⋅ H, d₂ = 20 mm - 2 ⋅ (5 / 8) ⋅ 1,732 mm = 17,835 mm.

Gwinty M6 mają średnicę główną (zewnętrzną) 6 mm. Zazwyczaj oznaczenia gwintów metrycznych zawierają również skok gwintu, tak więc śruba z gwintem M6 × 1 ma podstawową średnicę główną 6 mm i skok gwintu 1 mm. Kupując gwintowany element złączny, upewnij się, że masz zarówno taką samą średnicę, jak i skok gwintu. Jeśli jeden z tych wymiarów nie będzie kompatybilny, śruba nie zostanie poprawnie dopasowana.

Średnica nominalna gwintu to średnica, dla której gwint jest znany. Używamy średnicy nominalnej do ogólnej identyfikacji gwintów. Na przykład gwinty o oznaczeniu M10 × 1,5 mają średnicę nominalną 10 mm. Ogólnie rzecz biorąc, średnica nominalna gwintu jest taka sama jak zewnętrzna średnica gwintu.