Kalkulator arcsin (arcus sinus)

Z naszym kalkulatorem arcsin (czyli kalkulatorem funkcji odwrotnej do sinusa) nie będzie problemu ze znalezieniem arcusa sinusa w danym zadaniu. Po prostu wprowadź wartość sinusa dla trójkąta, a kalkulator wskaże wynik. Jedyną rzeczą, o której musisz pamiętać, jest ograniczona dziedzina arcsin (-1 ≤ sin ≤ 1).

Jeśli zastanawiasz się, czym jest arcus sinus lub jak wygląda wykres arcsin, nie czekaj dłużej — przewiń w dół, a odpowiedzi znajdziesz w naszym artykule! Zamieściliśmy również krótki akapit na temat cech funkcji arcsin, takich jak związek między całką i pochodną. Czas na naukę!

Arcsin lub arcus sinus jest funkcją odwrotną do funkcji sinus. Innymi słowy, pomaga znaleźć kąt trójkąta o znanej wartości sinusa:

arcsin(x) = y ⇔ x = sin(y)

Ponieważ dziedziną sinusa dla liczb rzeczywistych jest [-1, 1], możemy obliczyć arcsin tylko dla liczb z tego przedziału. To oznacza, że dziedziną arcsin (dla wyników rzeczywistych) jest -1 ≤ x ≤ 1.

Jednakże warto pamiętać, że sinus jest funkcją okresową, więc istnieje wiele liczb, które mają tę samą wartość sinusa. Na przykład sin(0) = 0, ale także sin(π) = 0, sin(2π) = 0, sin(-π) = 0 i sin(-326π) = 0. Dlatego, jeśli ktoś chce obliczyć arcsin(0), odpowiedzią może być 0, 2π (360°) lub -π (-180°), a to tylko kilka opcji! Wszystkie są poprawne, ale zwykle podajemy tylko jedną liczbę, którą chcemy obliczyć w danym zadaniu.

Arcsin(x) jest najczęściej stosowaną notacją, ponieważ sin^-1x może prowadzić do nieporozumień (ponieważ sin^-1x ≠ 1/sin(x)). Skrót asin(x) jest zwykle używany w językach programowania komputerowego.

Ponieważ podstawowa funkcja sinus nie jest funkcją różnowartościową, jej dziedzina musi zostać ograniczona, aby zapewnić, że arcsin pozostanie funkcją. Zazwyczaj wybieraną dziedziną jest -π/2 ≤ y ≤ π/2. Oznacza to, że zakres wartości funkcji odwrotnej będzie równy dziedzinie funkcji głównej; zatem zakres wartości funkcji arcsin wynosi [-π/2,π/2], a dziedzina funkcji arcsin to przedział [-1,1]. Poniżej znajdziesz wykres funkcji arcsin(x), a także kilka często używanych wartości arcsin:

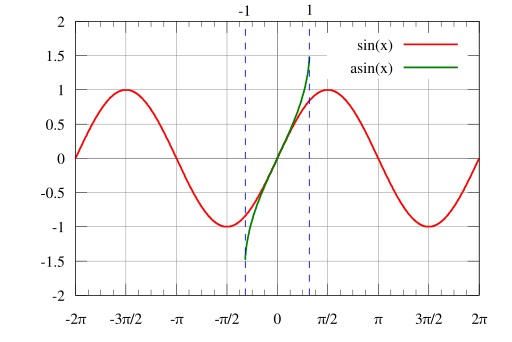
A oto jak wygląda wykres arcsin(x):

Zależności między funkcjami trygonometrycznymi i arcusem sinusem mogą pomóc ci jeszcze lepiej zrozumieć ten temat. Trójkąt prostokątny o przeciwprostokątnej długości 1 jest dobrym punktem wyjścia w nauce tych zależności.

Krótkie przypomnienie: dla trójkąta prostokątnego funkcja sinus przyjmuje kąt θ jako argument i zwraca stosunek przyprostokątnej do przeciwprostokątnej, który jest równy x w naszym przykładowym trójkącie. Funkcja odwrotna do funkcji sinus — arcsin, przyjmie stosunek przyprostokątnej do przeciwprostokątnej (x) i zwróci kąt θ. Wiedząc więc, że dla naszego trójkąta arcsin(x) = θ, możemy również napisać, że:

• Sinus: sin(arcsin(x)) = x
• Cosinus: cos(arcsin(x)) = √(1-x²)
• Tangens: tg(arcsin(x)) = x / √(1-x²)

Inne użyteczne zależności z arcusem sinusem to:

• arcsin(x) = π/2 - arccos(x)
• arcsin(-x) = -arcsin(x)

Czasami potrzebne są również całka i pochodna arcsin:

• Całka z arcsin: ∫arcsin(x) dx = x arcsin(x) + √(1 - x²) + C
• Pochodna arcsin: d/dx arcsin(x) = 1 / √(1 - x²) gdzie x ≠ -1, 1

Arcsin to funkcja, która jest przydatna na przykład do znajdowania kąta trójkąta prostokątnego. Jeśli szukasz kątów w trójkącie prostokątnym i znasz długości boków, dobrze znane twierdzenie Pitagorasa nie byłoby tak pomocne. Znalezienie kątów trójkąta prostokątnego wymaga zastosowania arcusa sinusa:

• dla α: sin(α) = a / c, więc α = arcsin(a / c)
• dla β: sin(β) = b / c, więc β = arcsin(b / c)

Załóżmy więc, że mamy dwie wartości podane w trójkącie prostokątnym, a = 6 i c = 10, i chcielibyśmy znaleźć wartość kąta α:

1. Wprowadź wartość, dla której chcesz znaleźć arcus sinus. W naszym przypadku jest to 6/10. Możesz więc wprowadzić wartość jako 0,6, ale forma 6/10 również będzie działać. Pamiętaj tylko, że wartość powinna zawierać się w przedziale od -1 do 1.
2. I… to wszystko! Kalkulator arcsin wykonał swoją pracę. Teraz wiesz, że arcsin(6/10) = 36,87°.

arcsin(1) = π/2 (= 90°). Arcsin jest funkcją odwrotną do funkcji sin. Ponieważ sin(π/2) = 1, arcsin(1) = π/2.

Tak, arcsin i sin⁻¹ odnoszą się do funkcji odwrotnej do funkcji sin. W rzeczywistości sin⁻¹() to inny sposób na oznaczenie funkcji arcsin. Jednak arcsin jest częściej używanym symbolem.

Znalezienie arcsin o wartości x polega na znalezieniu takiego kąta θ w trójkącie prostokątnym, w którym x jest stosunkiem boku przeciwległego do tego kąta θ do przeciwprostokątnej trójkąta.

Funkcja arcsin jest odwrotną funkcją trygonometryczną. Aby obliczyć wartość arcsin(x), wykonaj następujące kroki:

1. Znajdź wykres funkcji arcsin w zakresie [-1,1].

2. Znajdź punkt na krzywej arcsin taki, którego współrzędna x jest równa x.

3. Znajdź współrzędną y tego punktu. Wartość współrzędnej y jest równa arcsin(x).

4. Sprawdź wynik za pomocą Omni kalkulatora arcsin.