Kalkulator trygonometryczny

Omni kalkulator trygonometryczny pomoże ci w dwóch popularnych przypadkach, gdy potrzebna jest wiedza z zakresu trygonometrii. Jeśli chcesz znaleźć wartości funkcji sinus, cosinus, tangens i ich odwrotności, skorzystaj z pierwszej części kalkulatora. Szukasz brakującego boku lub kąta w trójkącie prostokątnym za pomocą trygonometrii? Nasze narzędzie to również bezpieczny wybór! Wpisz 2-3 podane wartości w drugiej części kalkulatora, a odpowiedź znajdziesz w mgnieniu oka. Przewiń w dół, jeśli chcesz dowiedzieć się więcej o trygonometrii i jej zastosowaniach.

Istnieje wiele innych przydatnych narzędzi do rozwiązywania problemów związanych z trygonometrią. Sprawdź dwa popularne prawa trygonometryczne za pomocą kalkulatora twierdzenia sinusów 🇺🇸 i kalkulatora twierdzenia cosinusów 🇺🇸, które pomogą ci rozwiązać każdy rodzaj trójkąta.

Ten kalkulator trygonometryczny ma dwie sekcje, które mają dwie różne funkcjonalności trygonometryczne. Poniższe instrukcje powinny pomóc ci z łatwością poruszać się po tym kalkulatorze:

1. Pierwsza sekcja wymaga wprowadzenia kąta i wyświetla listę wartości funkcji trygonometrycznych dla tego kąta. Aby wprowadzić inną jednostkę, kliknij jednostkę, aby ją zmienić, a następnie wprowadź kąt.

Na przykład, aby znaleźć wartość sin(45°), wystarczy wpisać 45 stopni jako kąt. Kalkulator natychmiast powie ci, że sin(45°) jest równy 0.70710678. Podaje on również wartości innych funkcji trygonometrycznych, takich jak cos(45°) i tg(45°).

2. W drugiej części wykorzystasz trygonometrię do wyznaczenia brakujących parametrów trójkąta prostokątnego:

   1. Najpierw wybierz, jakie parametry trójkąta są znane. Możesz wybrać pomiędzy „dwoma bokami”, „kątem i jednym bokiem” oraz „polem i jednym bokiem”.

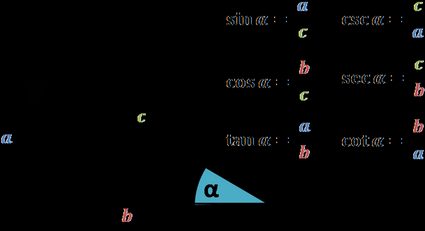
   2. Zapoznaj się z diagramem na dole kalkulatora, aby dowiedzieć się, co oznaczają etykiety parametrów (a, b, c). Wprowadź parametry zgodnie z dokonanym wyborem. Jeśli chcesz wprowadzić parametr w innej jednostce, zmień jednostkę przed wprowadzeniem wartości.

   3. Narzędzie obliczy brakujące parametry przy użyciu trygonometrii.

Na przykład załóżmy, że znamy dwa boki, a = 7 cm i b = 12 cm. Wprowadźmy je do tego kalkulatora. Od razu widzimy, że c = 13,892 cm, α = 30,256° i β = 59,74°.

Możemy również użyć tej sekcji w odwrotnej kolejności! Załóżmy, że znamy kąt β = 30°, b = 10 cm i c = 20 cm. Najpierw wpisz β = 30°, a natychmiast dowiemy się, że α = 60°. Teraz wprowadź b = 10 cm (upewniając się, że jednostką są centymetry). Podobnie, wprowadź c = 20 cm, a zobaczymy, że a = 17.32 cm.

Jeśli zastanawiasz się, w jaki sposób trygonometria może pomóc ci dowiedzieć się tak wiele o trójkątach, czytaj dalej ten artykuł. Znajdziesz w nim odpowiedzi na wiele pytań, które powinni znać wszyscy, którzy dopiero zaczęli uczyć się trygonometrii.

Trygonometria jest gałęzią matematyki. Samo słowo pochodzi od greckiego trigōnon (co oznacza „trójkąt”) i metron („miara”). Jak sama nazwa wskazuje, trygonometria zajmuje się przede wszystkim kątami i trójkątami; w szczególności definiuje i wykorzystuje relacje oraz stosunki między kątami i bokami w trójkątach. Podstawowym zastosowaniem jest więc rozwiązywanie trójkątów, zwłaszcza trójkątów prostokątnych, ale również każdego innego.

Trygonometria ma mnóstwo zastosowań: od problemów życia codziennego, takich jak obliczanie wysokości lub odległości między obiektami, po system nawigacji satelitarnej, astronomię i geografię. Ponadto, funkcje sinus i cosinus mają fundamentalne znaczenie dla opisywania zjawisk okresowych — dzięki nim możemy opisywać ruchy oscylacyjne (jak w naszym kalkulatorze wahadła prostego) i fale, takie jak dźwięk, wibracje czy światło.

Wiele dziedzin nauki i inżynierii wykorzystuje trygonometrię i funkcje trygonometryczne np. muzyka, akustyka, elektronika, medycyna i obrazowanie medyczne, biologia, chemia, meteorologia, elektrotechnika, mechanika, inżynieria lądowa, a nawet ekonomia… Funkcje trygonometryczne są naprawdę wszędzie wokół nas!

Aby znaleźć brakujące boki lub kąty trójkąta prostokątnego, wystarczy wprowadzić znane zmienne do naszego kalkulatora trygonometrycznego. Potrzebne są tylko dwie wartości w przypadku:

• jednego boku i jednego kąta,
• dwóch boków,
• powierzchni i jednego boku.

Pamiętaj, że jeśli znasz dwa kąty, nie wystarczy znaleźć boki trójkąta. Dwa trójkąty o tym samym kształcie (co oznacza, że mają równe kąty) mogą mieć różne rozmiary (ale nie te same długości boków) — ten rodzaj zależności nazywany jest podobieństwem trójkątów. Jeśli boki mają taką samą długość, to trójkąty są przystające.