Kalkulator objętości graniastosłupa trójkątnego

Nasz kalkulator objętości graniastosłupa trójkątnego to proste narzędzie, które może rozwiązać wszystkie twoje problemy związane z tym tematem — przy użyciu jednej z 6 dostępnych metod z 6 różnymi zestawami danych. 📐

Po zapoznaniu się z poniższym artykułem — nie tylko odkryjesz, jaki jest wzór na objętość graniastosłupa trójkątnego, ale także zapoznasz się z obliczeniami stojącymi za wszystkimi wynikami.

Przygotuj się — pomożemy ci zrozumieć proces obliczania objętości graniastosłupa trójkątnego. 🤓

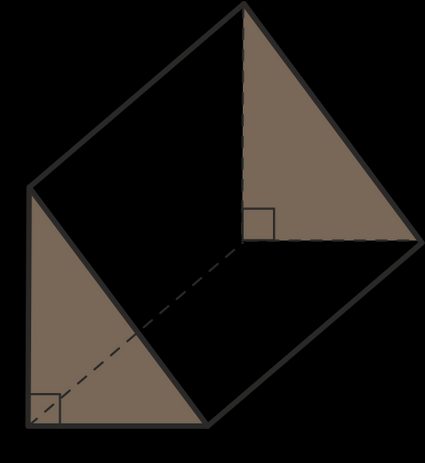
Graniastosłup trójkątny to bryła, której obie podstawy są trójkątne. Graniastosłup trójkątny jest wielościanem z trójkątami jako podstawami i prostokątami jako ścianami bocznymi.

Jak więc znaleźć objętość graniastosłupa trójkątnego za pomocą naszego narzędzia? To tak prostsze, niż się wydaje — od wyniku dzielą cię zaledwie sekundy!

1. Wybierz typ obliczania powierzchni trójkąta

   Zweryfikuj dane zawarte w zadaniu i sprawdź, które wartości są już podane:

   • ▲ Podstawa i wysokość — Znasz już długość podstawy i wysokość trójkąta;
   • ◣ Trójkąt prostokątny — Twój trójkąt zawiera kąt prosty (90°) między dwoma ramionami i znasz długości tych ramion;
   • ▲ 3 boki — Znasz długości wszystkich trzech boków trójkąta;
   • ▲ 2 boki + kąt między nimi — Znasz długości dwóch boków i wartość kąta między nimi;
   • ▲ 2 kąty + bok między nimi — Znasz wartość dwóch kątów trójkąta i długość boku między nimi; oraz
   • ▲ Powierzchnia ściany trójkąta — Idealna opcja, jeśli jesteś o krok do przodu i znasz już pole trójkątnej podstawy swojego graniastosłupa.

2. Wprowadź wszystkie dane podane w zapytaniu

   Możesz wybierać spośród 11 różnych jednostek — nie wahaj się ich mieszać!

3. Twoje wyniki zostaną wyświetlone 🎉

Łatwo poszło, prawda? Co powiesz na wypróbowanie naszych innych kalkulatorów geometrycznych:

🔺 Trójkąty:

• kalkulator graniastosłupa trójkątnego
• kalkulator pola powierzchni graniastosłupa trójkątnego

♦️ Prostokąty:

• kalkulator prostopadłościanu
• kalkulator objętości prostopadłościanu
• kalkulator pola powierzchni prostopadłościanu

Jak już wspomnieliśmy, istnieje 6 metod dostępnych w naszym kalkulatorze, służących obliczeniu objętości graniastosłupa trójkątnego. Szybko przejrzyjmy każdą z nich.

1. ▲ Podstawa i wysokość

   To jest podstawowe równanie objętości graniastosłupa trójkątnego:

   Objętość = 1/2 × Długość podstawy × Wysokość podstawy × Wysokość graniastosłupa

   gdzie:

   • Długość podstawy i Wysokość podstawy są wartościami trójkątnej podstawy graniastosłupa; oraz
   • Wysokość graniastosłupa to odległość między dwiema podstawami.

2. ◣ Trójkąt prostokątny

   Prawdopodobnie najpopularniejszy typ graniastosłupa.

   Wzór na objętość tego graniastosłupa wygląda następująco:

   Objętość = Wysokość ⋅ ((a ⋅ b) / 2)

   gdzie:

   • a i b to boki trójkąta, które dotykają kąta prostego; oraz
   • Wysokość to długość całego graniastosłupa, tj. odległość między dwiema podstawami.

   Aby obliczyć bok c w podstawie, użyj twierdzenia Pitagorasa.

3. ▲ 3 boki

   Objętość = 1/4 ⋅ √( (a+b+c) ⋅ (-a+b+c) ⋅ (a-b+c) ⋅ (a+b-c) ) ⋅ Wysokość

   Gdzie:

   • √ — oznacza pierwiastek kwadratowy wszystkich pomnożonych sum boków trójkąta (x² = y, √y = x);
   • a, b i c to boki trójkąta w podstawie; oraz
   • Wysokość to długość całego graniastosłupa, tj. odległość między dwiema podstawami.

4. ▲ 2 boki + kąt pomiędzy

   Objętość = 1/2 ⋅ a ⋅ b ⋅ sin(γ) ⋅ Wysokość

   gdzie:

   • sin(γ) — sinus kąta γ (użyj tablicy trygonometrycznej i naszego kalkulatora twierdzenia sinusów, aby zrozumieć podstawy tego równania);
   • a i b są bokami trójkąta, które dotykają kąt γ;
   • kąt γ — jego wartość musi zawierać się w przedziale od 0 do 180 stopni; oraz
   • Wysokość — długość całego graniastosłupa, tj. odległość między dwiema podstawami.

5. ▲ 2 kąty + bok pomiędzy

   Objętość = 1/2 ⋅ a ⋅ ((a ⋅ sin(β))/ sin(β + γ)) ⋅ sin(γ) ⋅ Wysokość

   gdzie:

   • sin — sinus danego kąta. Znalezione w tablicy trygonometrycznej, w oparciu o twierdzenie sinusów (jak wspomniano powyżej);
   • a — bok trójkąta, który dotyka zarówno kąta γ, jak i kąta β;
   • kąt γ — jego wartość musi zawierać się w przedziale od 0 do 180 stopni;
   • kąt β — jego wartość musi zawierać się w przedziale od 0 do 180 stopni; oraz
   • Wysokość — długość całego graniastosłupa, tj. odległość między dwiema podstawami.

6. ▲ Pole powierzchni podstawy

   Najlepsze rozwiązanie jest dostępne, jeśli znasz już powierzchnię trójkąta podstawy.

   Objętość = Pole podstawy × Wysokość

   gdzie:

   • Pole podstawy podawane jest w jednostkach pola, np. centymetrach kwadratowych (cm²), metrach kwadratowych (m²) lub kilometrach kwadratowych (km²); oraz
   • Wysokość jest długością całego graniastosłupa, tj. odległością między dwiema podstawami.