Kalkulator średniego tempa zmian

Kalkulator średniego tempa zmian jest tutaj, aby pomóc ci zrozumieć prostą koncepcję ukrytą za długą, nieco mylącą nazwą. Czym jest tempo zmian? Ogólnie rzecz biorąc, pokazuje zależność między dwoma czynnikami. Poniżej znajdziesz bardziej precyzyjną definicję średniego tempa zmian. Zademonstrujemy i wyjaśnimy również wzór na Średnie tempo zmian wraz z kilkoma przykładami jego zastosowania.

Wolisz oglądać niż czytać? Dowiedz się wszystkiego, czego potrzebujesz w 90 sekund dzięki temu filmowi, który stworzyliśmy dla ciebie:

Wszystko jest w ciągłym ruchu. Zmiana jest nieunikniona. Począwszy od przyspieszenia twojego roweru lub samochodu, poprzez wzrost populacji, od przepływu krwi w twoich żyłach do symbiozy twoich komórek, tempo zmian pozwala nam ustalić wartość związaną z tymi zmianami.

Średnie tempo zmian to szybkość, która opisuje, jak jedna liczba zmienia się w stosunku do drugiej. Jeśli masz funkcję liniową, jest to nachylenie linii narysowanej między dwoma punktami. Nie myl go jednak z nachyleniem. Możesz użyć średniego tempa zmian dla dowolnej funkcji, nie tylko liniowej.

Na poniższym rysunku zaznaczyliśmy dwa punkty, aby pomóc ci lepiej zrozumieć, jak znaleźć średnie tempo zmian.

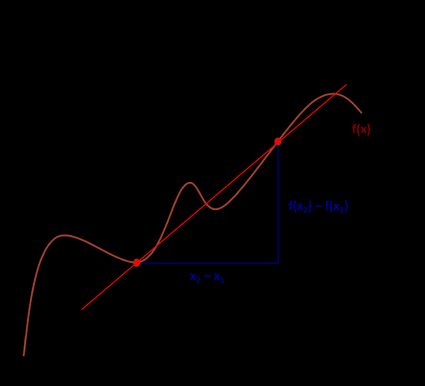
Wzór na średnie tempo zmian to:

A = [f(x₂) - f(x₁)] / [x₂ - x₁]

gdzie:

• (x₁, f(x₁)) — współrzędne pierwszego punktu; oraz
• (x₂, f(x₂)) — współrzędne drugiego punktu.

Jeśli wartość współrzędnej jest dodatnia, oznacza to, że jedna współrzędna rośnie wraz ze wzrostem drugiej. Na przykład, im więcej jeździsz na rowerze, tym więcej kalorii spalasz.

Jeśli wartość współrzędnej jest równa zero, gdy jedna współrzędna się zmienia, ale druga nie. Dobrym przykładem może być nieuczenie się do egzaminów. Gdy czas zaczyna się kończyć, ilość rzeczy do nauczenia się nie zmienia się.

Średnie tempo zmian jest ujemne, gdy jedna współrzędna rośnie, a druga maleje. Powiedzmy, że wybierasz się na wakacje. Im więcej czasu spędzasz w podróży, tym bliżej jesteś celu.

Oblicz średnie tempo zmian odległości (średnią prędkość) pociągu jadącego z Paryża do Rzymu (1420,6 km). Na poniższym wykresie możesz zobaczyć zmianę odległości w czasie:

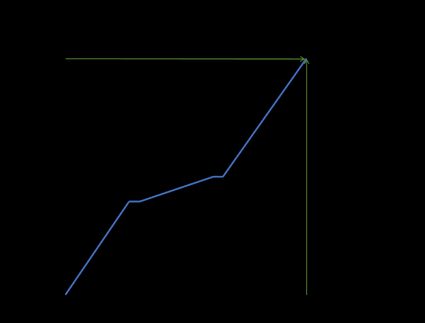
Jak widzisz, prędkość nie była stała. Pociąg zatrzymał się dwa razy, a pomiędzy przystankami jechał znacznie wolniej. Ale do obliczenia średniej prędkości jedynymi zmiennymi, które mają znaczenie, są zmiana odległości i zmiana czasu. Jeśli więc współrzędne pierwszego punktu to (0, 0), a współrzędne drugiego punktu to odległość między dwoma miastami, a czas podróży to (1420,6, 12,5), to:

A = (1420,6 - 0) / (12,5 - 0) = 113,648 [km/h]

Pociąg jechał ze średnią prędkością 113,648 kilometrów na godzinę. Spójrzmy teraz na bardziej matematyczny przykład.

Mamy pewną funkcję:

f(x) = x² + 5x - 7

Znajdźmy więc średnie tempo zmian w przedziale [-4, 6].

1. Najpierw trzeba znaleźć wartości funkcji dla obu punktów:

   f(x₁) = f(-4) = (-4)² + 5 × (-4) - 7 = -11

   f(x₂) = f(6) = 6² + 5 × 6 - 7 = 59

2. Następnie skorzystać z równania średniego tempa zmian:

   A = [f(x₂) - f(x₁)] / [x₂ - x₁] = [f(6) - f(-4)] / [6 - (-4)] = [59 - (-11)] / [6 - (-4)] = 70 / 10 = 7

Jeśli spodobał ci się kalkulator średniego tempa zmian, zapraszamy do zapoznania się z naszymi innymi narzędziami, takimi jak kalkulator odległości, gdzie można znaleźć odległość między punktami lub liniami.