Kalkulator sześciokąta

Witamy w kalkulatorze sześciokąta, naszym niezwykle użytecznym narzędziu gdy masz do czynienia z dowolnym sześciokątem foremnym. Czy wiesz, że sześciokąt foremny jest jednym z najbardziej popularnych kształtów w naszym życiu? Występuje w plastrach miodu jak i sześciokątnych płytkach do luster — jego zastosowania są niemal nieograniczone.

W poniższym artykule podamy definicję sześciokąta, wyjaśniamy popularność tego kształtu oraz nauczymy cię poprawnie rysować sześciokąty. Z naszym kalkulatorem sześciokątów poznasz wiele właściwości geometrycznych i nauczysz się, jak wyznaczyć m.in. pole sześciokąta.

Nie powinno być zaskoczeniem, że sześciokąt ma dokładnie sześć boków. Jest to własność, która definiuje tę figurę. Długości boków mogą być różne, a gdy są równe, to mamy do czynienia z sześciokątem foremnym. Kąty wewnętrzne sześciokąta sumują się do 720º - możesz je łatwo przeliczyć na inne jednostki za pomocą naszego przelicznika kątów 🇺🇸.

Nieco później dowiemy się, jak znaleźć pole sześciokąta foremnego. Na razie wystarczy wiedzieć, że sześciokąt foremny jest najczęściej spotykanym typem sześciokąta: zarówno w przyrodzie, jak i w zadaniach domowych ;).

Jedną z kolejnych sekcji poświęcimy w całości ważnym właściwościom sześciokąta foremnego, ale najpierw musimy dokładniej przedyskutować, czym jest sześciokąt foremny. Odpowiedź na to pytanie pomoże nam zrozumieć sztuczki, których możemy używać, aby obliczyć pole sześciokąta ze zrozumieniem, a nie bezmyślnie stosując wzór na pole sześciokąta. Sztuczki te polegają na wykorzystaniu własności innych wielokątów, takich jak kwadraty, trójkąty, czy równoległoboki.

Jak już sygnalizowaliśmy wyżej, w sześciokącie foremnym wszystkie boki muszą mieć tę samą długość oraz wszystkie kąty muszą być równe. Oczywiście każda długość boków jest dozwolona (o ile wszystkie są takie same), zatem dla sześciokąta foremnego obliczenie obwodu jest tak proste, że nie musisz nawet używać kalkulatora obwodu wielokąta 🇺🇸. Wystarczy obliczyć:

• obwód = 6 × bok

gdzie bok oznacza długość boku twojego sześciokąta foremnego.

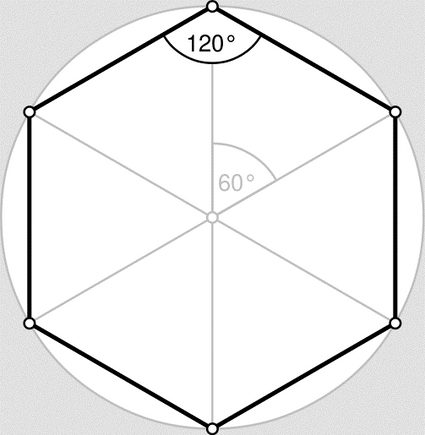
Jeśli chodzi o kąty, sześciokąt foremny ma mieć wszystkie kąty równe. Sumują się one do 720º, co oznacza, że każdy kąt musi mieć 120º.
Ten fakt okazuje się być niezwykle istotny, gdy zastanawiamy się nad powszechnością sześciokąta foremnego w przyrodzie. Będzie on pomocny również do zrozumienia, jak znaleźć pole sześciokąta foremnego.

Przyjrzymy się teraz, jak znaleźć pole sześciokąta przy użyciu różnych metod. Najprostszym sposobem jest oczywiście użycie naszego kalkulatora sześciokąta, który zawiera wbudowane narzędzie do przeliczania powierzchni na różne jednostki. Chcesz zrozumieć jak znaleźć pole sześciokąta foremnego? Doskonale!

Wzór na pole powierzchni wielokąta foremnego jest zawsze taki sam, niezależnie od tego, ile nasz wielokąt ma boków:

pole = apotema × obwód / 2.

Dla przypomnienia, apotema to promień okręgu wpisanego w wielokąt foremny, czyli odległość między środkiem wielokąta i środkowym punktem dowolnego boku.
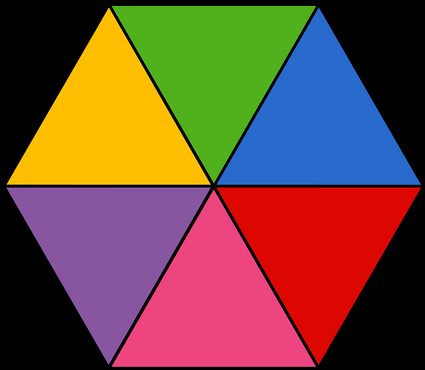
W sześciokącie foremnym jest to po prostu wysokość trójkąta równobocznego utworzonego z jednego boku i dwóch promieni okręgu opisanego na sześciokącie (te trójkąty to kolorowe obszary na powyższym obrazku).

Jeśli nie pamiętasz wzoru, zawsze możesz wyobrazić sobie sześciokąt jako 6 trójkątów. W przypadku sześciokąta foremnego trójkąty te są trójkątami równobocznymi, dzięki czemu łatwo jest obliczyć ich pole — znacznie łatwiej, niż gdyby były to trójkąty równoramienne (lub nawet trójkąty 45 45 90 jak w przypadku kwadratu).

W trójkącie równobocznym wszystkie boki mają taką samą długość (jest to też długość boku naszego sześciokąta foremnego). Będziemy ją oznaczać a. Wysokość trójkąta wynosi zatem h = √3/2 ∙ a. Jest to dokładnie wartość apotemy! (Przypominamy, że √ oznacza pierwiastek kwadratowy.) Mając ten wzór, możemy przystąpić do działań matematycznych:

• P₀ = a ∙ h / 2
• = a ∙ √3/2 ∙ a / 2
• = √3/4 ∙ a².

Gdzie P₀ oznacza pole każdego z trójkątów równobocznych, na które podzieliliśmy nasz sześciokąt. Po pomnożeniu tego pola przez 6 (bo mamy sześć trójkątów), otrzymujemy wzór na pole powierzchni sześciokąta foremnego:

• P = 6 ∙ P₀ = 6 ∙ √3/4 ∙ a²

• P = 3 ∙ √3/2 ∙ a²

• = (√3/2 ∙ a) ∙ (6 ∙ a) / 2

• = apotema × obwód / 2

Teraz już wiesz, skąd bierze się wzór na pole sześciokąta, który podaliśmy wcześniej!

Jeśli masz ochotę na nieco matematycznej egzotyki, możesz pobawić się innymi podziałami sześciokąta. Na przykład, możesz podzielić sześciokąt na pół (od wierzchołka do wierzchołka). W takim przypadku otrzymujemy dwa trapezy i możemy obliczyć pole sześciokąta jako ich sumę. Możesz również połączyć dwa sąsiednie trójkąty, aby skonstruować w sumie trzy różne romby i obliczyć powierzchnię każdego z nich osobno. Możesz nawet rozłożyć sześciokąt na jeden duży prostokąt (używając krótkich przekątnych) i 2 trójkąty równoramienne!

Nie wahaj się skorzystać z różnych kształtów i odpowiadających im Omni kalkulatorów, aby wymyślić jeszcze inne ciekawe podziały. Czy potrafisz obliczyć pole sześciokąta foremnego, używając tylko trójkątów prostokątnych? A może tylko specjalnych trójkątów prostokątnych jak trójkąty 30 60 90 oraz 45 45 90?

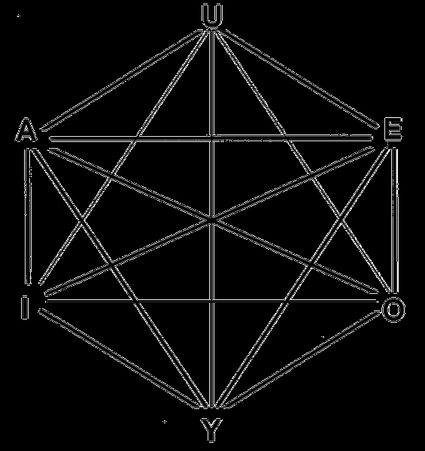
Sześciokąt foremny ma 9 przekątnych — trzy z nich to długie przekątne, przechodzące przez środek figury, a pozostałe sześć to tzw. wysokości sześciokąta. Nasz kalkulator sześciokąta oszczędzi ci żmudnych obliczeń dotyczących długości przekątnych sześciokąta foremnego. Jeśli jednak ciekawi cię, jak obliczyć długości przekątnych, to oczywiście też to wyjaśnimy.

• Długie przekątne — powstają przez połączenie dwóch wierzchołków, które mają pomiędzy sobą dokładnie dwa wierzchołki. Jak można zauważyć na powyższym rysunku, długość takiej przekątnej jest równa dwóm długościom krawędzi sześciokąta:

  D = 2 ∙ a

• Krótkie przekątne — powstają przez połączenie dwóch wierzchołków, które mają pomiędzy sobą dokładnie jeden wierzchołek. Ich długość jest równa:

  d = √3 ∙ a

Kolejne dwie liczby, które są ważne w sześciokącie foremnym, to promienie okręgu opisanego i wpisanego. Przypomnijmy, że okrąg opisany przechodzi przez wszystkie wierzchołki sześciokąta foremnego, zaś okrąg wpisany jest styczny do każdego boku.

• Aby znaleźć promień okręgu opisanego na sześciokącie foremnym, należy wyznaczyć odległość między punktem centralnym sześciokąta (który jest jednocześnie środkiem okręgu) a dowolnym z wierzchołków. Jest ona po prostu równa R = a.

• Promień okręgu wpisanego w sześciokąt foremny jest równy połowie jego wysokości (krótszej przekątnej), czyli równy apotemie: r = √3/2 ∙ a.

Teraz omówimy bardzo praktyczne zagadnienie: jak skonstruować sześciokąt foremny. Dla dowolnego (nieregularnego) sześciokąta odpowiedź jest prosta: narysuj dowolny wielokąt o sześciu bokach i gotowe. W przypadku sześciokąta foremnego sprawa nie jest jednak tak prosta, ponieważ musimy mieć pewność, że wszystkie boki są tej samej długości!

Aby uzyskać idealny efekt, będziesz potrzebować nie tylko linijki, ale też cyrkla. Narysuj dowolny okrąg, a następnie, zachowując ten samym promień, pozaznaczaj krótkie łuki na tym okręgu. Możesz zacząć od dowolnego miejsca, a po narysowaniu łuku przesuń punkt zaczepienia (igłę cyrkla) w miejsce, gdzie łuk przecina się z okręgiem. Wyznaczysz w ten sposób 6 punktów (miejsc przecięcia łuków z okręgiem), a gdy połączysz je odcinkami, otrzymasz sześciokąt foremny. Na powyższej animacji możesz przyjrzeć się, jak ten proces przebiega i... do dzieła!

Nasze narzędzie pozwala na obliczenie wielu parametrów sześciokąta foremnego. Korzystanie z niego jest tak proste, jak to tylko możliwe: jeden parametr wystarczy, aby obliczyć wszystkie pozostałe. Kalkulator zawiera też wbudowane narzędzie do przeliczania jednostek!

Omówimy teraz wszystkie parametry kalkulatora:

• Długość boku – Odległość między dwoma sąsiednimi wierzchołkami;
• Obwód – Suma długości wszystkich boków sześciokąta;
• Pole – Powierzchnia zamknięta przez sześciokąt foremny;
• Długa przekątna – Odległość od jednego z wierzchołków do przeciwległego wierzchołka;
• Krótka przekątna – Odległość między dwoma wierzchołkami, między którymi znajduje się jeden wierzchołek;
• Promień okręgu opisanego – Odległość od środka figury do każdego wierzchołka (promień sześciokąta); oraz
• Promień okręgu wpisanego – Odległość od środka figury do każdego boku (apotema).

Każdy kocha praktyczne zastosowania matematyki w świecie rzeczywistym, a sześciokąty są zdecydowanie jednym z najczęściej używanych wielokątów na świecie. Najprostszym (i prawdopodobnie najmniej ekscytującym) zastosowaniem są pakietaże sześciokątne. Sześciokąty są doskonałym kształtem, ponieważ idealnie pasują do siebie i wspaniale pokrywają każdą powierzchnię. Są przy tym mniej banalne niż kwadraty. Jeśli jesteś zainteresowany takim zastosowaniem, polecamy kalkulator podłóg oraz kalkulator powierzchni, ponieważ są to narzędzia skonstruowane specjalnie by ci w tym pomóc.

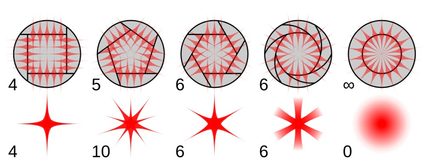
Kolejne zastosowanie jest wspólne dla wszystkich wielokątów, ale i tak jest bardzo ciekawe. W fotografii otwór matrycy prawie zawsze ma kształt wielokąta. Ta część aparatu nazywa się przysłoną i to ona odpowiada za liczne cechy zdjęć robionych danym aparatem. Najbardziej nieoczekiwaną z nich jest kształt bardzo jasnych (punktowych) obiektów, spowodowany efektem zwanym siatką dyfrakcyjną. Jest on zilustrowany na powyższej ilustracji.

Jednym z najbardziej wartościowych obszarów współczesnych zastosowań sześciokątów, ściśle związanym z tym, o czym mówiliśmy wyżej odnośnie fotografii, jest astronomia. Poważnym problemem, na jaki napotykamy podczas obserwacji odległych gwiazd jest to, jak słabo są one widoczne na nocnym niebie. Dzieje się tak dlatego, że mimo iż są to bardzo jasne obiekty, to znajdują się tak daleko od nas, że dociera do nas tylko niewielka część ich światła; więcej na ten temat dowiesz się z naszego kalkulatora jasności 🇺🇸. Na dodatek, z powodu efektów relatywistycznych (podobnych do dylatacji czasu i skrócenia długości), ich światło dociera do Ziemi z mniejszą energią niż zostało wyemitowane. Efekt ten nazywany jest przesunięciem ku czerwieni.

W efekcie dociera do nas niewielka ilość energii o większej długości fali niż byśmy chcieli. Najlepszym sposobem zaradzenia temu jest budowanie jak największych teleskopów. Problem w tym, że wykonanie jednoczęściowego zwierciadła większego niż kilka metrów jest prawie niemożliwe, nie mówiąc już o problemach z logistyką. Rozwiązaniem jest zbudowanie modułowego zwierciadła przy użyciu sześciokątnych segmentów takich jak te, które widzisz na zdjęciach powyżej.

Użycie tak dużego zwierciadła poprawia rozdzielczość kątową teleskopu oraz współczynnik powiększenia dzięki własnościom geometrycznym tzw. teleskopu Cassegraina. Możemy więc powiedzieć, że dzięki sześciokątom foremnym widzimy lepiej, dalej i wyraźniej, niż moglibyśmy to kiedykolwiek zrobić, stosując w teleskopach jedynie jednoczęściowe zwierciadła.

Czy wiesz, że istnieją również narzuty patchworkowe składające się z setek sześciokątów foremnych? Dowiedz się więcej dzięki Omni kalkulatorowi narzut patchworkowych z sześciokątów 🇺🇸!

Jak wiemy, wzór plastra miodu składa się z regularnych sześciokątów ułożonych obok siebie. Wypełniają one całkowicie dostępną powierzchnię, nie ma więc między nimi żadnych otworów. Wzór plastra miodu pojawia się w plastrach miodu (niespodzianka!), ale także w wielu innych obiektach w przyrodzie. Jest tak popularny, że można powiedzieć, iż jest to domyślny kształt, gdy w grę wchodzą rywalizujące ze sobą siły, a natura problemu wyklucza zastosowanie okręgów (lub sfer).

Od pszczelich uli do pęknięć skał, poprzez chemię organiczną (nawet w podstawowym budulcu życia: białkach), sześciokąty foremne są najbardziej powszechnym kształtem wielokątnym występującym w przyrodzie. I jest ku temu powód: wewnętrzne kąty sześciokątów. Kąt 120º jest najbardziej ze wszystkich kątów stabilny mechanicznie. Pod tym kątem spotykają się boki sześciokątów**, gdy ustawimy je obok siebie. Jeśli chcesz dowiedzieć się więcej o znaczeniu i zaletach sześciokątów foremnych, zachęcamy do obejrzenia tego filmu.

Sposób, w jaki kąty 120º rozkładają siły (i w konsekwencji naprężenia) na dwa boki sześciokąta sprawia, że jest to bardzo stabilna i mechanicznie wydajna struktura. Jest to istotna zaleta sześciokątów. Inną ważną własnością sześciokątów foremnych jest to, że mogą one wypełnić powierzchnię bez żadnych przerw między nimi (tzw. parkietaż, podobną własność mają trójkąty równoboczne i kwadraty). Ponadto sześciokąt foremny ma najmniejszy obwód przy największej powierzchni wśród wielokątów wypełniających powierzchnię, co czyni go bardzo wydajnym kształtem.

Fascynującym przykładem są też bańki mydlane, omówione w tym filmie. Kiedy tworzysz bańkę używając wody, mydła i własnego oddechu, zawsze ma ona kulisty kształt. Wynika to z tego, że objętość kuli jest największa ze wszystkich innych obiektów o danej powierzchni.

Jeśli jednak ułożymy bańki na płaskiej powierzchni, kula traci swoją przewagę wydajności, ponieważ okręgi (przekroje kuli) nie mogą całkowicie pokryć dwuwymiarowej przestrzeni. Tak się składa, że następny w kolejności najlepszy kształt (pod względem stosunku objętości do powierzchni) jest również najlepszy w równoważeniu napięcia między bańkami, które powstaje na ich powierzchni. Mowa oczywiście o naszym ulubionym sześciokącie foremnym.

Bańki są ciekawym sposobem wizualizacji zalet sześciokąta nad innymi kształtami, ale nie jedynym. W naturze, jak już wspomnieliśmy, istnieje mnóstwo przykładów formacji sześciokątnych, głównie z powodów związanych z naprężeniami i napięciami w materiale. Nie mamy miejsca, by omówić szczegółowo wszystkie z nich, ale możemy przynajmniej kilka z nich wymienić:

• plastry miodu;
• organiczne związki chemiczne;
• formacje baniek mydlanych i bąbelków;
• formacje skalne (jak Grobla Olbrzyma w Irlandii Północnej);
• oczy owadów; i wiele innych!