Calculadora de Regressão Exponencial

A calculadora de regressão exponencial da Omni está aqui para te ajudar sempre que precisar determinar o modelo de regressão exponencial de um conjunto de dados, ou, em outras palavras, para encontrar a curva exponencial de melhor ajuste.

O que é regressão exponencial? Continue lendo, pois não apenas fornecemos a você a fórmula de regressão exponencial, mas também explicamos como calcular a regressão exponencial e em quais situações o ajuste exponencial tem utilidade. Como bônus, mostramos como derivar a equação de regressão exponencial para que você não precise decorá-la. 😉

O objetivo da regressão exponencial é encontrar uma curva exponencial que melhor se ajuste a um determinado conjunto de dados. Isso é muito semelhante a outros modelos de regressão, que você pode descobrir por meio das ferramentas da Omni:

• Calculadora de mínimos quadrados 🇺🇸, onde procuramos a linha (reta) de melhor ajuste;
• Calculadora de regressão quadrática 🇺🇸, em que você procura o ajuste de uma parábola;
• Calculadora de regressão cúbica 🇺🇸 trata das curvas cúbicas (ou seja, grau três) de melhor ajuste; e
• Calculadora de regressão polinomial 🇺🇸, onde procuramos a curva polinomial de melhor ajuste.

Há muitas situações em que os dados não seguem nem uma linha reta nem uma parábola, mas uma curva exponencial parece ser o ajuste a ideal; esses são processos que crescem lentamente no início e depois se aceleram rapidamente ou cujo decaimento começa rapidamente e depois se torna mais lento com o passar do tempo. Os exemplos incluem o crescimento do investimento, as temperaturas de objetos resfriados e o decaimento radioativo.

Seja x a variável explicativa e y a variável de resposta. A equação da regressão exponencial é y = a ⋅ b^x, em que a ≠ 0 e b > 0, b ≠ 1. Os coeficientes a e b devem ser escolhidos de forma que a equação corresponda à curva exponencial de melhor ajuste para o conjunto de dados, (x₁, y₁), ..., (x_n, y_n):

Na próxima seção, mostraremos a você como encontrar os coeficientes a e b. Mas antes, vamos discutir o significado deles aqui:

• a é o valor previsto pelo modelo de regressão exponencial para x = 0;
• Se b > 1, o ajuste exponencial descreve um crescimento exponencial; e
• Se 0 < b < 1, o ajuste exponencial descreve um decaimento exponencial.

Observe que temos a ⋅ b^x+1 = a ⋅ b ⋅ b^x, portanto, se x aumenta em 1 unidade, então y é multiplicado por b. Isso contrasta fortemente com a regressão linear y = m ⋅ x ⋅ c, em que um aumento em x de 1 unidade resulta no valor de m (inclinação) sendo adicionado a y!

Discutimos a equação de ajuste exponencial, mas como você pode calcular a regressão exponencial depois de coletar alguns dados? O truque é:

1. Transformar nossos dados para que eles permitam um modelo linear.
2. Determinar esse modelo linearmente, por exemplo, com o método dos mínimos quadrados.
3. Transformar os dados e o modelo de volta à forma original.

A fórmula da regressão exponencial para os dados (x, y) é:

y = exp(c) ⋅ exp(m ⋅ x)

onde m é a inclinação e c é a interceptação do modelo de regressão linearmente ajustado aos dados (x, ln(y)). Consulte a próxima seção para verificar os detalhes da derivação.

Com o modelo de regressão exponencial, procuramos explicar nossos dados com a ajuda da equação na forma y = a ⋅ bˣ. Aqui, mostraremos a você como a fórmula da regressão exponencial pode ser derivada. Para determinar os coeficientes a e b, siga estas etapas:

1. Tome o logaritmo de ambos os lados da equação; temos a seguinte equação equivalente:

   ln(y) = ln(a ⋅ bˣ)

2. As propriedades dos logaritmos fornecem:

   ln(y) = ln(a) + ln(bˣ)

   e

   ln(y) = ln(a) + x ⋅ ln(b)

3. Expressamos ln(y) como uma função linear de x, com inclinação ln(b) e interceptação ln(a).

4. Encontre a reta de melhor ajuste para (x, ln(y)). Digamos que você considere ln(y) = c + x ⋅ m.

5. Procure por a e b que satisfaçam

   ln(a) = c e ln(b) = m

6. Para calcular a e b, tome a exponencial (antilogaritmo) da inclinação m e do intercepto c:

   a = exp(c) e b = exp(m)

1. Insira seus dados na calculadora. Você pode inserir até 30 pontos de dados (novas linhas aparecerão à medida que você preencher os campos). Lembre-se de que precisamos de pelo menos 3 pontos (em ambas as coordenadas!) para ajustar um modelo.

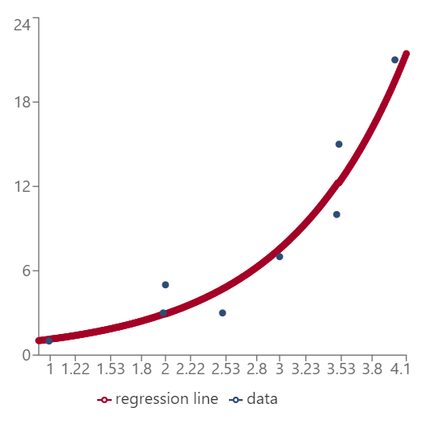
2. Você verá um gráfico de dispersão com seus dados, juntamente com a curva exponencial de melhor ajuste.

3. Abaixo do gráfico, você pode encontrar a equação da regressão exponencial para seus dados.

4. Se necessário, vá para o Modo Avançado para aumentar a precisão (número de algarismos significativos) com a qual o coeficiente é calculado. A precisão padrão é definida como 4 algarismos significativos.

A fórmula para a função exponencial é f(x) = a ⋅ b^x ou f(x) = ab^x, onde a é o coeficiente, b é a base e x é o expoente. Isso se aplica quando a ≠ 0 e b > 0, b ≠ 1.

Para calcular a regressão exponencial, você precisa:

1. Transformar seus dados para que eles permitam um modelo linear.
2. Determinar o modelo linear específico usando o método dos mínimos quadrados.
3. Transformar os dados e o modelo de volta à forma original.

R² é o coeficiente de determinação na regressão exponencial. Em outras palavras, o valor de R² indica o grau de precisão com que a reta de regressão representa os pontos de dados. Quanto mais próximo R² estiver de 1, mais precisa é a regressão.

A taxa de variação de y baseada em x é diferente. Na regressão linear, a alteração de y é uma adição constante, enquanto na regressão exponencial, a alteração de y é uma multiplicação constante.

Por exemplo, o valor de y poderia aumentar em +3 na regressão linear ou ×3 na regressão exponencial, conforme mostrado na tabela:

Você pode usar a Desmos para traçar uma regressão exponencial:

1. Insira seus pontos de dados (x₁ e y₁, etc.) inserindo-os em uma tabela ou colando-os do Excel.
2. Os gráficos de dados aparecerão no gráfico da Desmos.
3. Insira sua equação exponencial ou modelo na próxima célula para criar uma linha de regressão exponencial no gráfico.
4. Pronto!