Calculadora de Tensão

Esta calculadora de tensão é uma ferramenta Omni que ensinará a você como encontrar a força de tensão em uma corda ou um fio usado para levantar um objeto. Neste artigo, você também pode aprender a encontrar a tensão em cordas usadas para puxar um objeto em uma superfície sem atrito. Você também verá nesta calculadora de tensão de corda, uma variedade de diagramas de corpo livre para entender melhor como calcular as forças de tensão. Se quiser saber mais sobre a tensão e a fórmula da força de tensão, continue lendo!

Imagine que você pegue uma bola de basquete do chão. Você sentirá o peso da bola nas suas mãos devido à força da gravidade agindo sobre a massa da bola. Agora imagine amarrar uma corda ao redor da bola, que você usará para levantá-la novamente. Você ainda sentiria o peso da bola por meio da corda. Nessa situação, a corda está agora em tensão. O que mantém a corda unida à bola é chamado de força de tensão. Ao cortar a corda, você liberará a força de tensão e colocará a bola em queda livre.

A força de tensão é uma força axial que passa por um objeto que puxa, como uma corda, um barbante ou uma corrente. Também podemos observar a força de tensão em outros materiais, como hastes e barras, uma vez que, eles são submetidos a cargas externas de puxar ou de tração. Os materiais com alta resistência à tração são as melhores hastes e barras, pois não se quebram facilmente quando submetidos a forças de tensão. Você pode consultar a nossa outra calculadora de tensão mecânica, que discute o conceito de elasticidade, para saber mais sobre resistência à tração.

A força de tensão também é um ótimo exemplo da terceira lei de Newton para o movimento. A terceira lei de Newton para o movimento afirma que, quando um corpo exerce uma força em um segundo corpo, o segundo corpo exerce uma força igual na direção oposta de volta ao corpo original. A força de tensão é uma força de reação que neutraliza uma força externa que puxa o objeto.

Para calcular a tensão que age em uma corda, primeiro precisamos entender a segunda lei de Newton para o movimento. Essa lei afirma que a soma das forças que agem em um objeto de massa constante é igual à massa desse objeto multiplicada por sua aceleração. Também podemos expressar essa afirmação como uma equação:

ΣF = m ⋅ a

onde:

• Σ: (sigma) denota a soma das forças F;
• m: massa do objeto; e
• a: aceleração.

Para um objeto suspenso por uma corda, podemos usar aceleração devido à gravidade 🇺🇸, g. A aceleração gravitacional nos dá o valor de seu peso em termos de força, medida em Newtons. Se o objeto estiver se movendo em uma aceleração diferente, devemos usar sua aceleração real para o cálculo. No entanto, essa calculadora de tensão determina apenas as forças de tensão em casos de equilíbrio estático.

Essa declaração significa que essa ferramenta considera apenas objetos em repouso em um determinado sistema. Além disso, também assumimos que as cordas não têm massa e, portanto, não contribuem com nada para as forças de tensão. Também presumimos que as massas ou os objetos estão em um vácuo e não sofrem atrito ou resistência do ar em relação aos seus arredores.

Podemos ver na ilustração abaixo que a força, F, necessária para levantar o objeto é igual ao peso, W, do objeto. Essa ideia é o conceito fundamental subjacente à nossa fórmula de força de tensão. Também vemos abaixo o diagrama de corpo livre do objeto, que mostra as forças de tensão, T, agindo na corda. Como você pode ver, as forças de tensão vêm em pares e em direções opostas:

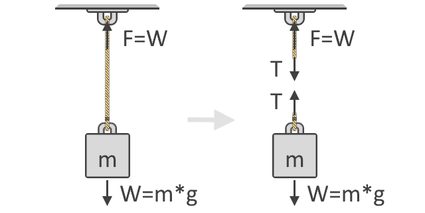
Seguindo a segunda lei de Newton, podemos então expressar a soma das forças usando o diagrama de corpo livre do objeto, conforme mostrado no lado direito da ilustração acima. Usamos diagramas de corpo livre para mostrar as diferentes direções e magnitudes das forças que agem em um corpo. Em equilíbrio, todas essas forças devem ser iguais a zero. Considerando todas as forças para cima como positivas e para baixo como negativas, nossa equação é:

ΣF↑ = 0 = T + (-W)

T = W

onde o peso, W, torna-se negativo, pois é direcionado para baixo. Colocando W do outro lado da equação, podemos ver agora que a força de tensão na corda é igual ao peso do objeto que ela carrega, como também mostrado acima.

Se usarmos mais cordas para levantar o objeto, a força de tensão total será dividida entre as cordas. A força de tensão em cada corda depende de seu ângulo em relação à direção da força à qual ela se opõe. Para entender melhor isso, vamos considerar outro diagrama de corpo livre de um objeto suspenso por duas cordas, conforme mostrado abaixo:

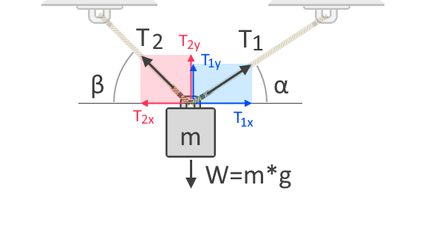
No diagrama de corpo livre mostrado acima, podemos ver as componentes horizontal e vertical das forças de tensão, T₁ e T₂. As forças são vetores, o que significa que sempre têm módulo, direção e sentido. Como todos os vetores, as forças podem ser expressas nessas componentes, que fornecem a influência da força ao longo dos eixos horizontal e vertical. T₁ₓ e T₂ₓ são as componentes horizontais de T₁ e T₂, respectivamente. Por outro lado, T_1y e T_2y são as componentes verticais das mesmas forças, respectivamente. Como a gravidade age sobre o objeto no eixo vertical, precisamos considerar as componentes verticais das forças de tensão para nossa soma de forças da seguinte forma:

ΣF↑ = 0 = T_1y + T_2y + (-W)

W = T_1y + T_2y

Como também conhecemos os ângulos das forças de tensão, podemos expressar T_1y e T_2y em termos de T₁ e T₂, respectivamente, com a ajuda de funções trigonométricas:

T_1y = T₁ × sen(α)

T_2y = T₂ × sen(β)

W = T₁ × sen(α) + T₂ × sen(β)

Você também pode dizer que, para que o sistema esteja em equilíbrio, o objeto não deve se mover horizontalmente ou ao longo do eixo x. Portanto, as componentes horizontais de T₁ e T₂ devem ser iguais a zero. Além disso, com a ajuda da trigonometria, podemos expressar T₁ₓ e T₂ₓ em termos de T₁ e T₂, respectivamente:

T₁ₓ = T₂ₓ

T₁ × cos(α) = T₂ × cos(β)

Se dividirmos ambos os lados por cos(α), obteremos uma equação na qual T₁ é expresso em termos de T₂ e dos ângulos:

T₁ = T₂ × cos(β) / cos(α)

Em seguida, podemos usar essa equação para resolver T₂ substituindo T₂ × cos(β) / cos(α) como T₁ em nossa equação de soma de forças, conforme mostrado abaixo:

W = T₁ × sen(α) + T₂ × sen(β)

W = T₂ × [cos(β) / cos(α)] × sen(α) + T₂ × sen(β)

W = T₂ × [cos(β) × sen(α) / cos(α) + sen(β)]

T₂ = W / [cos(β) × sen(α) / cos(α) + sen(β)]

Finalmente, se multiplicarmos toda essa equação por cos(β) / cos(α), como derivamos o valor de T₁ em termos de T₂, e depois simplificarmos tudo, obteremos esta equação:

T₁ = W / [cos(β) × sen(α) / cos(α) + sen(β)] × [cos(β) / cos(α)]

T₁ = W / [cos(β) × sen(α) / cos(α) + sen(β)] × [cos(β) / cos(α)]

T₁ = W / [cos(α) × sen(β) / cos(β) + sen(α)]

Agora, tudo o que você precisa saber são os ângulos dos cabos de tensão em relação à horizontal. Se você receber um ângulo da vertical, basta subtrair esse ângulo de 90°. Ao fazer isso, você obterá o ângulo em relação à horizontal. No entanto, se você tiver outros valores de ângulos que possam ser maiores que 90° ou mesmo 180°, talvez queira conferir nossa calculadora de ângulo de referência 🇺🇸 para ajudá-lo a determinar o ângulo necessário. Depois de determinar os valores das variáveis em nossas equações, você pode resolver as forças de tensão.

O procedimento para encontrar a força de tensão em um objeto que está sendo puxado é igual ao caso de um objeto que está pendurado. A única diferença é que primeiro precisamos computar a aceleração de todo o sistema e somar todas as forças ao longo da horizontal. Se a corda estiver em um ângulo em relação ao nível do solo, também precisaremos computar a componente horizontal da força de tensão.

Vamos dar uma olhada no exemplo abaixo para que você entenda melhor como encontrar a força de tensão em uma corda que puxa um ou dois objetos. Neste exemplo, dois objetos estão sendo puxados por uma única força de tensão aplicada. Outra corda está puxando o segundo objeto, que está preso ao primeiro objeto, como mostrado abaixo:

Esta ilustração mostra que as massas m₁ e m₂ possuem 3 kg e 2 kg, respectivamente. A soma dessas duas massas dá a massa total do sistema, 5 kg. Também precisamos determinar a componente horizontal da força tensão, T = 24 N, que está em um ângulo θ = 60°. Se usarmos as funções trigonométricas novamente, podemos dizer que o componente horizontal da força de tensão é igual a 24 N × cos(60°), que é igual a 12 N. Agora que conhecemos a componente horizontal da força de tensão e a massa total do sistema, podemos calcular a aceleração, a, da seguinte forma:

F = m ⋅ a → a = F / m

a = 12 N / 5 kg = 2,4 m/s²

Após encontrarmos a aceleração do sistema, podemos usar a segunda lei do movimento de Newton novamente para calcular a tensão da corda ou do fio do sistema. Para fazer isso, multiplique a aceleração pela massa que a corda está puxando. Para T₂, seu diagrama de corpo livre nos mostra que ele é responsável apenas pela massa m₂; podemos dizer que T₂ = a ⋅ m₂. Dito isso, T₂ = (2,4 m/s²) ⋅ (2 kg) = 4,8 N. Por outro lado, T₁ é a força de tensão que puxa tanto o peso m₁ quanto o de m₂. Entretanto, já temos o valor de T₁, que é simplesmente igual a T = 24,0 N. Portanto, T₁ = 24,0 N.

Em nosso exemplo, se as cordas esquerda e direita fossem apenas uma única corda, poderíamos comparar essa configuração a um sistema de polias. Uma polia é uma máquina simples que usa as forças de tensão nas cordas para obter vantagem mecânica. Você pode conferir nossas calculadora de polias e calculadora de comprimento de correia (que é um sistema de duas polias) para saber mais sobre vantagem mecânica e tensão.