Calculadora de Coeficiente Binomial

Bem-vindo à calculadora de coeficiente binomial da Omni, onde você terá a oportunidade de calcular e aprender tudo sobre a misteriosa fórmula n elementos agrupados k a k. A expressão indica o número de combinações de elementos k de um conjunto de elementos n e corresponde ao botão nCr em uma calculadora real.

Para saber a resposta da pergunta "O que é um binômio?", o significado de combinação, a solução para "4 elementos agrupados 2 a 2" e a comparação entre permutação e combinação, vá em frente e explore as seções abaixo!

Em matemática (álgebra, para ser mais preciso), um binômio é um polinômio com dois termos (é daí que vem o prefixo "bi-"). Por exemplo, as expressões x + 1, xy - 2ab ou x³z - 0,5y⁵ são todas binomiais, mas x⁵, a + b - cd ou x² - 4x² não são (a última tem dois termos, mas podemos simplificar essa expressão para -3x², que tem apenas um).

Agora que sabemos o que é um binômio, vamos examinar mais de perto como obter um expoente de um:

(x² - 3)³

Há alguns casos especiais dessa expressão, as fórmulas curtas de multiplicação que você deve conhecer da escola:

(a + b)² = a² + 2ab + b²,

(a - b)² = a² - 2ab + b².

O polinômio que obtemos no lado direito é chamado de expansão binomial do que tínhamos entre colchetes. Acredite ou não, podemos encontrar suas fórmulas para qualquer potência de número inteiro positivo. Em termos gerais, o teorema binomial nos diz como é essa expansão:

onde:

• $C_k$ é o número de todas as combinações possíveis de $k$ elementos de um $n$conjunto de elementos.

Além disso, para um dado n, os $C_k$'s são visualizados claramente através do chamado triângulo de Pascal, onde uma única linha na totalidade conta todos os subconjuntos possíveis do conjunto (ou seja, a cardinalidade do conjunto de potências). Visite nossa calculadora do triângulo de Pascal para gerar o triângulo de Pascal do tamanho que você quiser.

E este é um bom momento para verificarmos o significado de "combinação", que já mencionamos algumas vezes.

Imagine que você é um estudante universitário, tirando um cochilo casual durante uma palestra. De repente, o professor traz você de volta à Terra dizendo: "Vamos escolher aleatoriamente os grupos para os projetos do meio do semestre". Bem, parece que você não conseguirá escapar de fazer algum trabalho.

O problema é que só há um colega com quem você gostaria de trabalhar no projeto. Se houver vinte pessoas no grupo e o professor dividir vocês em grupos de quatro, qual é a probabilidade de você ficar com seu colega?

Cada grupo possível é um exemplo de uma combinação. Nesse caso, uma combinação de quatro elementos de um conjunto de vinte elementos ou, se você preferir, de quatro alunos de um grupo de vinte pessoas. Se você quiser ser um pouco mais técnico, escolher uma combinação significa escolher um subconjunto de um conjunto maior. O mais importante aqui é que a ordem dos elementos que escolhemos não importa. Afinal de contas, todos os membros de uma equipe de projeto são iguais (exceto aqueles que não fazem nenhum trabalho).

O número de combinações de k elementos de um conjunto de n elementos é denotado por

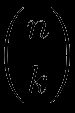
(como uma fração de n dividida por k, mas sem a linha no meio), que lemos como "n elementos agrupados k a k em todas as instâncias" Esse também é o símbolo que aparece quando escolhemos pressionar nCr em uma calculadora (não a nossa calculadora de coeficiente binomial, mas uma calculadora comum do dia-a-dia). Por exemplo,

é "4 elementos agrupados 2 a 2" e

é "6 elementos agrupados 2 a 2". Em alguns livros didáticos, o coeficiente binomial também é denotado por C(n,k), tornando-o uma função de n e k. "E como posso calculá-lo?" Bem, é bastante fácil. A fórmula de n elementos agrupados k a k é

n!/(k! × (n - k)!).

O ponto de exclamação é chamado de fatorial. A expressão n! é o produto dos primeiros n números naturais, ou seja,

n! = 1 ⋅ 2 ⋅ 3 ⋅ ... ⋅ n.

Isso significa, por exemplo, que 4 elementos agrupados 2 a 2 é

4! / (2! ⋅ (4 - 2)!) = (1 ⋅ 2 ⋅ 3 ⋅ 4) / (1 ⋅ 2 ⋅ 1 ⋅ 2) = 6,

e que 6 elementos agrupados 2 a 2 é

6! / (2! ⋅ (6 - 2)!) = (1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6) / (1 ⋅ 2 ⋅ 1 ⋅ 2 ⋅ 3 ⋅ 4) = 15.

Para saber mais sobre fatoriais, visite nossa calculadora de fatorial 🇺🇸!

Portanto, temos seis maneiras de escolher dois elementos de um conjunto de quatro, e quinze maneiras de fazer o mesmo para um conjunto de seis.

Antes de prosseguirmos, vamos dar mais uma olhada na fórmula n elementos agrupados k a k. Podemos obter dela uma propriedade simétrica bastante interessante.

Se tomarmos n agrupados n - k a n - k, iremos obter

n! / ((n - k)! × (n - (n - k))!) = n! / ((n - k)! × k!)

que é o mesmo que n elementos agrupados k a k (já que a multiplicação é comutativa). Em outras palavras, temos

ou C(n,k) = C(n,n-k) na outra notação.

Na seção anterior vimos o que é um fatorial. Em análise combinatória, ele denota o número de permutações. Uma permutação de comprimento n significa colocar n elementos em alguma ordem. Por exemplo, se tivermos três expressões de gatinhos fofos, digamos 😹, 😻 e 🙀, poderemos ordená-los de seis maneiras diferentes:

(😹, 😻, 🙀)

(😹, 🙀, 😻)

(😻, 😹, 🙀)

(😻, 🙀, 😹)

(🙀, 😹, 😻)

(🙀, 😻, 😹).

Observe que isso está de acordo com a definição de fatorial:

3! = 3 ⋅ 2 ⋅ 1 = 6.

Visite a calculadora de permutação 🇺🇸 para se aprofundar ainda mais neste assunto.

Observe que podemos entender essa fórmula da seguinte maneira: escolhemos o primeiro elemento dentre três (3 opções), o segundo dentre os dois restantes (porque já escolhemos um - 2 opções) e o terceiro dentre o que resta (porque já escolhemos dois - 1 opção). Multiplicamos o número de opções: 3 ⋅ 2 ⋅ 1 = 6, e obtemos o fatorial.

Quando comparamos permutação e combinação, a palavra-chave é ordem. Como dissemos na seção anterior, o significado por trás de uma combinação é escolher alguns elementos de uma coleção maior. Em essência, dizemos quais escolhemos, mas não qual é o primeiro, o segundo, etc. Eles formam um conjunto na totalidade.

Uma permutação, no entanto, coloca os elementos em uma ordem fixa, um após o outro, tornando-a uma sequência em vez de um conjunto. Além disso, uma permutação usa todos os elementos do conjunto que você obteve, enquanto uma combinação escolhe apenas alguns deles.

Como exemplo, mais uma vez, coloque-se no lugar do estudante universitário. Quando o professor escolheu o grupo para você, ele escolheu uma combinação. E quando chega a hora de apresentar seu projeto e eles fazem uma pergunta para cada um de vocês, eles escolhem uma permutação (determinando a ordem em que fazem as perguntas). Todos nós sabemos como a ordem pode ser importante para a nota final.

Os coeficientes binomiais são uma das sequências de números mais importantes em matemática discreta e em análise combinatória. Eles aparecem com muita frequência em cálculos de estatística e probabilidade e talvez sejam os mais importantes na distribuição binomial (incluindo a distribuição binomial negativa 🇺🇸). Isso significa que somente os matemáticos nerds têm algum uso real para isso?

Nem sempre! Todo jogo de azar é baseado no acaso, e os coeficientes binomiais são o fator vital. Um simples lançamento de moeda é o exemplo mais fácil, o qual você pode calcular com outra ferramenta da Omni: a calculadora de probabilidade no lançamento de moedas. No entanto, vamos dar um passo adiante e analisar o pôquer.

Você já se perguntou por que algumas mãos no pôquer são mais valiosas do que outras? Isso acontece simplesmente porque elas são mais raras (a menos que alguém esteja trapaceando, mas já vimos séries de TV de gângsteres suficientes para saber que isso geralmente é uma má ideia).

Há 52 cartas em um baralho normal em que um jogador recebe cinco cartas. Nossa calculadora de coeficiente binomial e a fórmula n elementos agrupados k a k (no nosso caso com n = 52 e k = 5), nos diz que isso se traduz em 2.598.960 mãos possíveis em um jogo de pôquer. Bastante coisa, concorda? E agora considere a melhor mão possível, um royal flush em paus (Ás, Rei, Rainha, Valete e 10). Essa mão pode acontecer somente em um caso, quando obtivermos exatamente estas cartas. Isso significa que você tem uma 1 em 2.598.960 chances de tê-la. Não recomendamos que você aposte todas as suas economias nessas probabilidades.

Vejamos outro exemplo: um full house (três cartas do mesmo tipo e um par). Dessa vez, há consideravelmente mais possibilidades. Afinal, qualquer uma das 13 cartas de um naipe pode ser uma trinca e o par está em uma das outras 12 cartas (não pode ter o mesmo valor que a trinca). Além disso, a trinca está em apenas três dos quatro símbolos de cartas e, da mesma forma, o par está em apenas dois.

E é aí que nos lembramos do significado de uma combinação! Precisamos escolher três de quatro símbolos para a trinca e uma combinação de dois de quatro para o par. A fórmula n elementos agrupados k a k traduz isso em 4 agrupado 3 a 3 e 4 agrupado 2 a 2, e a calculadora de coeficiente binomial conta que eles são 4 e 6, respectivamente. Assim, se agora multiplicarmos os números que obtivemos, descobriremos que há

13 ⋅ 12 ⋅ 4 ⋅ 6 = 3.744

mãos possíveis que dão um full house. Bem, não são muitas em comparação com todas as possibilidades, mas pelo menos é 3.744 vezes mais provável do que o royal flush em paus.

Ainda assim, sugerimos que você economize seu dinheiro ao invés de usá-lo em apostas.