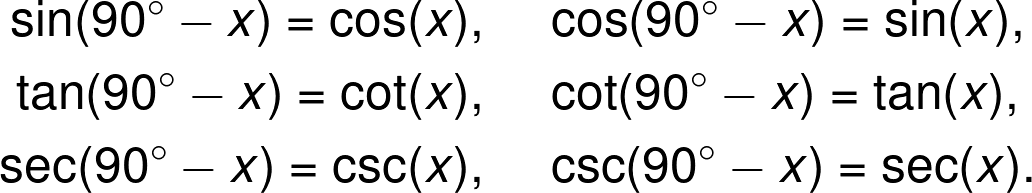Calculadora de Cofunção
Boas-vindas à calculadora de cofunção da Omni, onde estudaremos as funções trigonométricas de ângulos complementares, e veremos também como usá-las. Em essência, na trigonometria, há seis funções que descrevem completamente as relações entre os ângulos e os lados de um triângulo. Essas funções estão conectadas umas às outras através de ângulos complementares, por isso, costumamos pensar nelas como pares: sen e cos, tan e cot, sec e csc. Hoje, examinaremos essas relações e aprenderemos como passar de uma função para seu par, ou seja, sua cofunção.
Portanto, sente-se, relaxe e desfrute de uma boa matemática!
Funções trigonométricas
Antes de vermos o que é uma cofunção, precisamos começar com o básico. Na geometria, não podemos ser mais básicos do que os triângulos: três lados, três vértices, três ângulos internos. De certa forma, não pode haver polígono mais simples.
No entanto, estamos mais interessados em um tipo específico de triângulo: triângulos retângulos (você sabe, aqueles sobre os quais o teorema de Pitágoras trata). Um de seus ângulos é sempre (daí o nome), portanto, já temos algumas informações sobre nossa forma mesmo antes de desenhá-la.
Além disso, podemos observar algumas outras dependências que fazem com que o triângulo tenha a aparência que tem. Afinal, se aumentarmos um dos ângulos agudos, podemos ver facilmente que o lado oposto também terá de ficar mais longo. Essa observação é, mais ou menos, a ideia por trás da trigonometria: relacionar os ângulos internos de um triângulo com seus lados. Nós nos concentramos nesse tópico em nossa calculadora de trigonometria.
Além disso, devemos lembrar que a soma dos ângulos internos de qualquer triângulo é igual à , portanto, a soma dos ângulos agudos do triângulo retângulo vale . Quando a soma de dois ângulos é igual à eles são chamados de complementares.
Definimos funções trigonométricas como proporções entre os lados de um triângulo retângulo. Abaixo você pode encontrar uma figura com as fórmulas para todas as seis.
Observe como, na calculadora de cofunção, há uma identidade para cada uma delas.
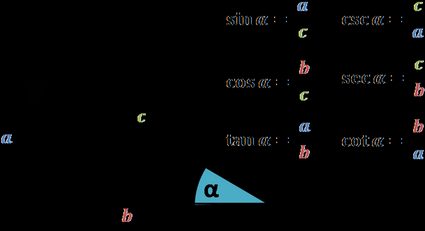
🔎 As funções trigonométricas (sen, cos, tan) são todas proporções. Portanto, você pode encontrar os termos ausentes usando nada mais do que a nossa calculadora de proporções!
Por exemplo, vemos que o seno é igual ao cateto oposto ao ângulo dividido pela hipotenusa. Observe como nunca mencionamos o tamanho do triângulo. De fato, é aí que reside uma propriedade crucial da trigonometria: mesmo se dimensionarmos o triângulo para o dobro de seu tamanho, se mantivermos os ângulos intactos, os valores das funções trigonométricas não mudarão.
Entretanto, as fórmulas acima, apesar de toda a sua beleza, têm uma falha importante. Nós as definimos usando um triângulo retângulo, de modo que o ângulo só pode estar entre e graus (ou e em radianos). Mas não fique de mau humor! Felizmente para nós, para a matemática e para o mundo todo, existe uma maneira de corrigir isso! A única coisa que precisamos fazer é traduzir o raciocínio para um espaço Euclidiano bidimensional, ou seja, o plano.
Seja um ponto no plano e o ângulo que vai no sentido anti-horário da metade positiva do eixo horizontal até o segmento de reta cujos pontos finais são e . Observe, como dissemos, que vai de uma reta para a outra e não que é simplesmente o ângulo entre elas. É por isso que geralmente chamamos de ângulo direcionado.
Obviamente, agora pode ser maior que . De fato, pode até mesmo ir além de . Para esses ângulos, consideramos apenas o primeiro como a primeira volta em torno de e, a partir desse valor, continuamos com a segunda volta (e, se necessário, a terceira, a quarta, etc.). Na verdade, é ainda mais do que isso: também pode ser negativo. Afinal, dissemos que se trata de um ângulo direcionado, portanto, para valores negativos, simplesmente invertemos a direção, ou seja, seguimos no sentido horário em vez de anti-horário.
Agora que entendemos os ângulos de todos os tamanhos, podemos definir as funções trigonométricas para eles e para o ponto . A regra aqui é bem simples: repetimos as fórmulas da figura acima, mas substituímos por , por , e por , ou seja, a distância de a . Por exemplo, a secante agora terá a forma:
Ok, agora conhecemos as funções trigonométricas a partir de suas definições, portanto, estamos prontos para nos aprofundar no tema. Afinal, o nome “calculadora de cofunção” foi o que nos trouxe aqui, e ainda não sabemos como encontrar uma cofunção. Para isso, o melhor que podemos fazer é explorar os gráficos das funções.
Os gráficos da cofunção: sen e cos, tan e cot, sec e csc
As seis funções trigonométricas são seno e cosseno ( e ), tangente e cotangente ( e ) e secante e cossecante ( e ).
Você já deve ter percebido por que as emparelhamos da maneira que fizemos apenas pelos nomes. Em cada par, temos a função “básica” e outra função correspondente com o mesmo nome, mas com um prefixo adicional “co-”. A semelhança com a palavra “cofunção” está longe de ser coincidência. Em cada um dos pares, dizemos que uma é a cofunção da outra.
“Mas o que significa ser uma cofunção?” Bem, estamos felizes com a sua pergunta! Veremos as identidades da cofunção em detalhes na próxima seção. Primeiro, porém, vamos tentar entendê-las observando os gráficos das funções em pares e identificando as semelhanças.
Comecemos com seno e cosseno.
Eles parecem quase iguais, não é mesmo? O seno é apenas o cosseno, mas movido (ou em radianos) para a direita. Assim, podemos dizer que o seno de um ângulo é igual ao cosseno do ângulo complementar. O mesmo tipo de conexão ocorre entre as outras funções e cofunções trigonométricas.
Para nossos propósitos, vamos nos concentrar na área de a e imaginar que você está percorrendo essa distância ao longo das inclinações de ambas as curvas, mas em direções diferentes: O seno de para e o cosseno de para . Você consegue ver que os caminhos são os mesmos?
Falando em inclinações, a calculadora de inclinação da Omni pode ajudar você a entender este conceito. Não deixe de consultá-la se você estiver precisando!
Agora tentemos fazer algo semelhante para os gráficos de tangente e cotangente.
Novamente, se traçarmos a curva tangente de a e a cotangente de a , perceberemos que estamos seguindo um caminho semelhante.
Por fim, temos as funções sec e csc.

Como você deve ter adivinhado, a história se repete para a secante e a cossecante.
Em essência, isso é o que caracteriza as cofunções. Poderíamos dizer que seus gráficos são reflexos mútuos se colocarmos um espelho no ponto médio do intervalo , ou seja, em . Isso, por sua vez, significa que o valor de uma função trigonométrica em deve ser o mesmo que o valor da cofunção no ponto . E é exatamente isso que as identidades das cofunções afirmam.
Identidades das cofunções
Conforme mencionado na seção anterior, dividimos as funções trigonométricas em pares. Em cada um deles, uma é a cofunção da outra. Isso significa que seus gráficos (e, portanto, valores) são reflexos uns dos outros no intervalo . Portanto, o valor de um ponto na primeira função é o mesmo que o valor de na segunda função.
Se você quiser agradar a alguns cientistas, podemos escrever o parágrafo acima usando notação matemática:
No entanto, lembre-se de que elas funcionam somente para ângulos entre e . Observe que as fórmulas acima se baseiam no fato de que os ângulos de cada lado do sinal são complementares, ou seja, juntos eles formam .
Na verdade, existe uma maneira de considerar outros ângulos também. No entanto, isso é complicado. Aqui, tivemos a conveniência de que todas as funções admitem valores positivos no intervalo . Fora dele, os termos podem se tornar negativos. Além disso, surge a questão de onde colocar “o espelho”, que reflete as cofunções.
Apesar dos obstáculos, após horas de trabalho árduo, os matemáticos foram capazes de propor fórmulas que generalizam as identidades das cofunções. Elas são chamadas de fórmulas de redução trigonométrica (não é o mesmo conceito descrito na calculadora de redução de potência 🇺🇸, cuidado). Embora não as forneçamos aqui, incentivamos você a pesquisá-las e aproveitar um pouco mais de conhecimento matemático. Certamente é melhor do que passar horas e horas vendo memes!
E com isso, declaramos o fim da teoria por hoje! Já passamos um bom tempo aprendendo definições e fórmulas. Por que você não pega alguns exemplos e coloca as identidades da cofunção em uso?
Exemplo: usando a calculadora de cofunção
Digamos que você tenha decidido fazer algumas reformas na sua sala de estar.
Seu plano é consertar o piso e talvez substituir os azulejos por madeira. O problema é que você precisa das medidas, e o cômodo não é um retângulo perfeito; há algumas paredes inclinadas. Felizmente, você ainda se lembra de algumas coisas da faculdade e, depois de pensar um pouco, percebe que você precisará do cosseno de e da cotangente de para fazer outros cálculos.
No entanto, há um problema: já se passaram alguns anos desde a sua última aula de trigonometria e você não se lembra das fórmulas do cosseno ou da cotangente. O que você lembra é o seno e a tangente. Como a calculadora de cofunção se encaixa bem nesse cenário!
(Tudo bem, admitimos que os detalhes são um pouco rebuscados, mas, por favor, nos dê um desconto. A imaginação dos desenvolvedores de conteúdo da Omni também tem um limite).
Em primeiro lugar, vejamos como a tarefa é fácil quando você tem a calculadora de cofunção em mãos. Lá, começamos escolhendo a função que temos. Em primeiro lugar, escolhemos o cosseno, ou seja, , na lista. Assim que tivermos isso, passamos para o campo da variável abaixo, que contém o ângulo. Inserimos e, no momento em que fazermos isso, a calculadora de cofunção exibe a resposta abaixo, indicando tanto a cofunção como o valor. Da mesma forma, para o segundo caso, escolhemos a cotangente () na lista e inserimos .
Observe como, em cada um desses casos, a ferramenta nos dá um valor preciso (ou seja, na forma de uma fração com raiz quadrada) além do valor arredondado. Explicaremos por que isso acontece em um segundo momento. Além disso, embora a calculadora de cofunção busque a precisão, você pode querer reduzir o número de algarismos significativos na resposta para quaisquer outros cálculos.
Agora, vamos deixar a ferramenta da Omni de lado e ver como você pode encontrar a resposta por conta própria. Você seguirá as etapas abaixo:
- Desenhe um triângulo retângulo com o ângulo dado;
- Use as identidades de cofunção para transformar a função que estamos buscando em sua cofunção; e
- Calcule o valor da cofunção tomando as razões dos lados do triângulo.
Começamos com o ângulo de .
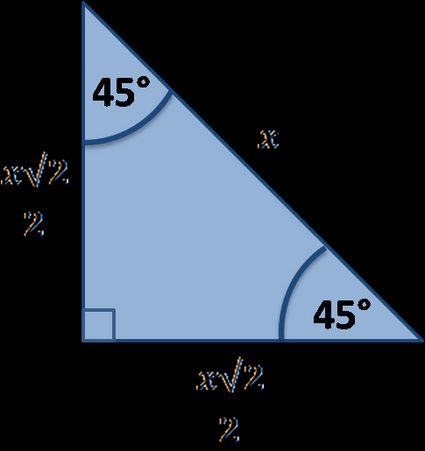
Observe que esse é um exemplo de triângulo bastante especial, para o qual conhecemos as relações entre os lados, ou seja, sabemos que se o lado tem comprimento , então, a hipotenusa deve ser . Isso ocorre porque nossa forma é, de fato, a metade de um quadrado, onde o lado maior é a diagonal do quadrado. A calculadora de triângulos retângulos especiais pode dizer a você mais sobre esse tipo de triângulo.
Agora, lembre-se das identidades de cofunção vistas na seção anterior e use-as para transformar em um seno:
Dessa forma, podemos aplicar a fórmula do seno para encontrar a resposta. Na primeira seção, dissemos que é o cateto oposto ao ângulo dividido pela hipotenusa. Isso dá:
Agora passemos para o caso . Novamente, começamos com um desenho.

Como antes, temos a sorte de conhecer as relações entre os lados. Desta vez, é porque nossa forma é, de fato, a metade de um triângulo equilátero.
Usamos as identidades de cofunção para transformar em uma tangente:
Observe que, embora o ângulo em questão tenha mudado, ainda podemos usar a mesma figura. Esse sempre será o caso das identidades de cofunção, pois estamos sempre lidando com ângulos complementares, ou seja, aqueles que formam os ângulos agudos do mesmo triângulo retângulo.
Por fim, lembramos da fórmula da tangente da primeira seção: a função retorna o lado oposto ao ângulo dividido pelo outro. No nosso caso, isso é:
Pronto! Encontramos as funções trigonométricas de que precisávamos; estamos prontos para cuidar desses azulejos e melhorar a sala de estar. Com certeza, ela ficará muito mais aconchegante quando você instalar a madeira compensada. E quando você terminar, por que não ir além e pensar na reforma para o quarto?
FAQ
Como usar as identidades da cofunção?
As identidades da cofunção permitem que você determine o valor de uma função trigonométrica dado o valor da cofunção (da sua função) no ângulo complementar ao seu ângulo. Por exemplo, você pode encontrar facilmente cos(20°) se souber sen(70°) porque o seno e o cosseno são cofunções e 70° + 20° = 90°.
Quanto vale x para satisfazer sen(x) = cos(15°)?
A resposta é x = 75°. Sabemos que o seno e o cosseno são cofunções, ou seja, seus valores concordam em ângulos complementares. Portanto, x e 15° devem ser complementares: x + 15° = 90°. Portanto, x = 75°, como afirmado.
Como encontrar o seno com o cosseno?
Para determinar sen(x) dado cos(x), siga estas etapas:
- Calcule o quadrado de
cos(x). - Subtraia
cos²(x)de1. - Pegue a raiz quadrada do resultado da etapa 2. Lembre-se de que há dois resultados possíveis: um positivo e um negativo.
- O que você tem são os dois valores possíveis de
sen(x). Se você sabe, por exemplo, que o ânguloxé agudo, então, seu seno é positivo. - A forma completa da identidade trigonométrica que aplicamos é
sen²(x) + cos²(x) = 1.
Como encontrar o seno com o cosseno e a tangente?
Para determinar o seno de um ângulo, dados o cosseno e a tangente, você precisa multiplicar o cosseno pela tangente. A fórmula que você precisa é:
sen(α) = tan(α) ⋅ cos(α)