Calculadora de Trigonometria

Essa calculadora de trigonometria da Omni ajudará você a resolver dois problemas nos quais os conceitos sobre trigonometria são necessários. Se você quiser encontrar os valores de seno, cosseno, tangente e suas funções recíprocas, use a primeira parte da calculadora. Você está procurando o lado ou o ângulo que falta em um triângulo retângulo usando a trigonometria? Nossa ferramenta também irá te ajudar! Forneça 2 ou 3 valores na segunda parte da calculadora e você encontrará a resposta em um piscar de olhos. Role a tela para baixo se quiser saber mais sobre trigonometria e onde você pode aplicá-la.

Há muitas outras ferramentas úteis quando você lida com problemas de trigonometria. Confira duas leis trigonométricas muito utilizadas com a calculadora da lei dos senos e a calculadora da lei dos cossenos da Omni. Elas ajudarão você a solucionar qualquer tipo de triângulo.

Esta calculadora de trigonometria tem duas seções que executam duas funções diferentes usando a trigonometria. As instruções a seguir devem ajudar você a usar esta calculadora com facilidade:

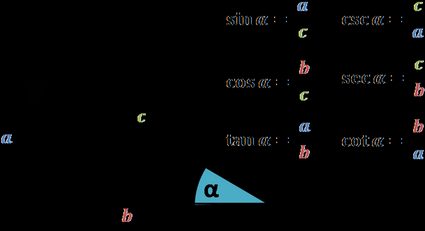
1. A primeira seção recebe um ângulo e fornece a você uma lista de valores de função trigonométrica para esse ângulo. Para inserir uma unidade diferente, clique na unidade para alterá-la e, em seguida, insira o ângulo.

Por exemplo, para encontrar o valor de sen(45°), basta inserir 45 graus como o ângulo. A calculadora informa instantaneamente a você que sen(45°) = 0,70710678. Ela também fornece a você os valores de outras funções trigonométricas, como cos(45°) e tan(45°).

2. A segunda seção usa a trigonometria para determinar os parâmetros ausentes de um triângulo retângulo:

   1. Primeiro, selecione quais parâmetros são conhecidos. Você pode escolher entre “dois lados”, “um ângulo e um lado” e “área e um lado”.

   2. Consulte o diagrama na parte inferior da calculadora para entender melhor a definição dos parâmetros. Insira os parâmetros de sua escolha. Se você precisar inserir um parâmetro em uma unidade diferente, altere a unidade antes de inserir o valor.

   3. A ferramenta calculará os parâmetros ausentes usando trigonometria.

Por exemplo, se você conhece dois lados, a = 7 cm e b = 12 cm, insira-os nessa calculadora. Imediatamente, você verá que c = 13,892 cm, α = 30,256° e β = 59,74°.

Também podemos usar essa seção de forma inversa! Digamos que você saiba que o ângulo β = 30° e b = 10 cm. Primeiro, digite β = 30°, e imediatamente você saberá que α = 60°. Agora, digite b = 10 cm. Imediatamente nossa calculará preencherá os outros campos, mostrando que c = 20 cm e a = 17,32 cm.

Se você está se perguntando como a trigonometria pode te ajudar a aprender tanto sobre triângulos, continue lendo este artigo. Ele responde a muitas perguntas que pessoas novas no mundo da trigonometria devem saber.

A trigonometria é um ramo da matemática. A palavra em si vem do grego trigōnon (que significa "triângulo") e metron ("medida"). Como o nome sugere, a trigonometria lida principalmente com ângulos e triângulos. Na verdade, ela define e usa as relações e proporções entre ângulos e lados em triângulos. A principal aplicação é, portanto, encontrar as medidas de um triângulo, sejam eles triângulos retângulos ou qualquer outro tipo de triângulo que você queira.

A trigonometria tem muitas aplicações: desde problemas do dia a dia, como o cálculo da altura ou da distância entre objetos, até o sistema de navegação por satélite, a astronomia e a geografia. Além disso, as funções seno e cosseno são fundamentais para a descrição de fenômenos periódicos. Graças a elas, podemos descrever movimentos oscilatórios (como em nossa calculadora de pêndulo simples) e ondas como som, vibração ou luz.

Muitos campos da ciência e da engenharia utilizam a trigonometria e as funções trigonométricas, entre eles: música, acústica, eletrônica, medicina e imagens médicas, biologia, química, meteorologia, engenharia elétrica, mecânica, civil e até mesmo economia... As funções trigonométricas estão realmente ao nosso redor!

Para encontrar os lados ou ângulos do triângulo retângulo, tudo o que você precisa fazer é inserir as variáveis conhecidas na calculadora de trigonometria. Você precisa fornecer pelo menos dois valores, que podem ser:

• um lado e um ângulo
• dois lados
• área e um lado

Lembre-se de que saber dois ângulos, não é suficiente para encontrar os lados do triângulo. Dois triângulos com a mesma forma (o que significa que eles têm ângulos iguais), podem ter tamanhos ou comprimentos de lados, diferentes. Esse tipo de relação é chamada de similaridade de triângulo. Se os lados tiverem o mesmo comprimento, então os triângulos são congruentes.

Olá, eu sou Hanna, a criadora desta calculadora de trigonometria, sou doutora em engenharia mecânica e mestre na criação de ferramentas científicas. Eu sabia que uma boa calculadora de trigonometria me ajudaria a obter a profundidade de campo certa para minhas fotografias, então me sentei para criá-la. Graças a ela, consegui tirar algumas fotos nítidas de lindos pássaros na natureza!

Dedicamos um cuidado extra à qualidade de nosso conteúdo para que ele seja o mais preciso e confiável possível. Cada ferramenta é revisada por um especialista treinado e, em seguida, revisada por um falante nativo. Para saber mais sobre nossos padrões, consulte a página de políticas editoriais.