Calculadora de Raiz Cúbica

A calculadora de raiz cúbica da Omni é uma ferramenta útil que ajudará você a determinar a raiz cúbica de qualquer número positivo. Você pode usar nossa calculadora imediatamente; basta digitar o número a partir do qual deseja encontrar a raiz cúbica e pronto! Além disso, você pode fazer os cálculos ao contrário e usar esta ferramenta para elevar números ao cubo. Para fazer isso, basta digitar o número que você deseja elevar a potência no último campo! Isso pode ser extremamente útil quando você estiver procurando pelos chamados cubos perfeitos 🇺🇸. Você pode ler mais sobre eles neste artigo.

Graças à nossa calculadora de raiz cúbica, você também pode calcular as raízes de outros graus. Para fazer isso, você precisa alterar o número no campo grau da raiz. Se você quiser saber mais sobre a definição de raiz cúbica, familiarizar-se com as propriedades da função de raiz cúbica e encontrar uma lista dos cubos perfeitos, recomendamos que continue lendo este texto. Nele, você também encontrará alguns truques sobre como encontrar a raiz cúbica em uma calculadora ou como calculá-la mentalmente.

Se você estiver interessado na história dos símbolos de raiz, vá para a nossa calculadora de raiz quadrada, onde discutimos isso.

Vamos supor que você queira encontrar a raiz cúbica de um número, x. A raiz cúbica, y, é um número que, se você elevar a terceira potência, terá x como resultado. Essa frase pode ser escrita matematicamente como:

∛x = y ⟺ y^3 = x

onde ⟺ é um símbolo matemático que significa se e somente se.

Você também pode escrever a raiz cúbica de uma maneira diferente, o que às vezes é muito mais conveniente. Isso ocorre porque a raiz cúbica é um caso especial de um expoente. Ela pode ser escrita como

∛(x) = x^(1/3)

Um exemplo geométrico pode ajudar você a entender isso. O melhor exemplo que podemos dar é o do cubo. Bem, a raiz cúbica do volume de um cubo é o comprimento de sua aresta. Assim, por exemplo, se um cubo tem um volume de 27 cm³, então o comprimento de suas arestas é igual à raiz cúbica de 27 cm³, que é 3 cm. Fácil?

Lembre-se de que, na maioria dos casos, a raiz cúbica não será um número racional. Esses números podem ser expressos como um quociente de dois números naturais, ou seja, uma fração. As frações podem trazer algumas dificuldades, especialmente quando se trata de somá-las. Se você estiver tendo problemas para trabalhar com frações, tente nossa calculadora de adição de frações 🇺🇸, que o ajudará nesta tarefa.

É muito fácil encontrar a raiz cúbica de qualquer número positivo com nossa calculadora de raiz cúbica! Basta digitar qualquer número para encontrar sua raiz cúbica. Por exemplo, a raiz cúbica de 216 é 6. Para ver a lista de cubos perfeitos, vá para a próxima seção deste artigo.

Observe que também é possível encontrar a raiz cúbica de um número negativo. Afinal de contas, um número negativo elevado à terceira potência ainda é negativo, por exemplo, (-6)³ = -216.

No entanto, você precisa lembrar que qualquer número diferente de zero tem três raízes cúbicas: pelo menos uma real e duas imaginárias. Essa calculadora de raiz cúbica lida apenas com números reais, mas se você estiver interessado, recomendamos que leia a seção mais abaixo intitulada "Três soluções da raiz cúbica", que aborda o tópico de números imaginários!

Você pode encontrar os valores mais comuns da raiz cúbica abaixo. Esses números também são frequentemente chamados de cubos perfeitos porque suas raízes cúbicas são inteiras. Aqui está a lista dos dez primeiros cubos perfeitos:

• raiz cúbica de 1: ∛1 = 1, já que 1 ⋅ 1 ⋅ 1 = 1;
• raiz cúbica de 8: ∛8 = 2, já que 2 ⋅ 2 ⋅ 2 = 8;
• raiz cúbica de 27: ∛27 = 3, pois 3 ⋅ 3 ⋅ 3 = 27;
• raiz cúbica de 64: ∛64 = 4, pois 4 ⋅ 4 ⋅ 4 = 64;
• raiz cúbica de 125: ∛125 = 5, pois 5 ⋅ 5 ⋅ 5 = 125;
• raiz cúbica de 216: ∛216 = 6, já que 6 ⋅ 6 ⋅ 6 = 216;
• raiz cúbica de 343: ∛343 = 7, já que 7 ⋅ 7 ⋅ 7 = 343;
• raiz cúbica de 512: ∛512 = 8, já que 8 ⋅ 8 ⋅ 8 = 512;
• raiz cúbica de 729: ∛729 = 9, já que 9 ⋅ 9 ⋅ 9 = 729;
• raiz cúbica de 1000: ∛1000 = 10, pois 10 ⋅ 10 ⋅ 10 = 1000;

Como você pode ver, os números se tornam muito grandes rapidamente, mas às vezes você terá de lidar com números ainda maiores, como fatoriais. Nesse caso, recomendamos que você use a notação científica, que é uma forma muito mais conveniente de escrever números muito grandes ou muito pequenos.

Por outro lado, a maioria dos outros números não são cubos perfeitos, mas alguns deles ainda são usados com frequência. Aqui está a lista de alguns dos cubos não perfeitos (arredondados até os centésimos):

• raiz cúbica de 2: ∛2 ≈ 1,26;
• raiz cúbica de 3: ∛3 ≈ 1,44;
• raiz cúbica de 4: ∛4 ≈ 1,59;
• raiz cúbica de 5: ∛5 ≈ 1,71;
• raiz cúbica de 10: ∛10 ≈ 2,15;

Não hesite em usar nossa calculadora de raiz cúbica se o número que você deseja e precisa não estiver nessa lista!

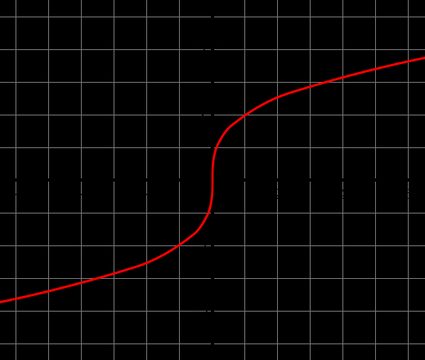
Você pode representar graficamente a função y = ∛(x). Ao contrário, por exemplo, da função logarítmica, a função raiz cúbica é uma função ímpar, o que significa que ela é simétrica com relação à origem e atende à condição - f(x) = f(-x). Essa função também passa por zero.

Graças a essa função, você pode desenhar um gráfico de raiz cúbica, que é mostrado abaixo. Também recomendamos que você confira a calculadora da fórmula quadrática 🇺🇸 para ver outras funções!

Você acha que é possível resolver problemas simples com raiz cúbica sem uma calculadora on-line ou mesmo lápis e papel? Se você acha que isso é impossível ou que é incapaz de fazer isso, confira este método, pois é muito fácil. No entanto, ele só funciona para cubos perfeitos. Esqueça todas as regras dos livros de aritmética e considere por um momento o seguinte método.

Antes de tudo, é essencial que você memorize os cubos dos números de 1 a 10 e o último dígito de seus valores. Você pode ver isso na tabela abaixo.

Quando você tem um número do qual deseja encontrar a raiz cúbica, olhe primeiro para os milhares (pule os três últimos dígitos). Por exemplo, para o número 185.193, os milhares são 185. O cubo de 5 é 125 e o de 6 é 216. Portanto, é óbvio que o número que você está procurando está entre 50 e 60. O próximo passo é ignorar todos os outros números, exceto o último dígito. Podemos ver que é 3, portanto, verifique sua memória ou nossa tabela. Você encontrará que o número que está procurando é 7. Portanto, a resposta é 57! Você acha que é fácil?

Vamos pegar outro exemplo e fazer isso passo a passo!

1. Pense no número que você quer saber como uma raiz cúbica. Vamos pegar 17576.
2. Pule os três últimos dígitos.
3. Encontre as duas raízes cúbicas mais próximas que você conhece. A raiz cúbica de 8 é 2, e a raiz cúbica de 27 é 3. Portanto, seu número está entre 20 e 30.
4. Observe o último dígito. O último dígito de 17576 é 6.
5. Verifique em sua memória (ou em nossa tabela), o último dígito 6 corresponde ao número 6. Esse é o último dígito de seu número.
6. Combine os dois: 26. Essa é a raiz cúbica de 17576!

Lembramos a você que esse algoritmo funciona apenas para cubos perfeitos! E a probabilidade de que um número aleatório seja um cubo perfeito é, infelizmente, muito baixa. Você tem apenas 0,0091 por cento de chance de encontrar um entre 1.000 e 1.000.000. Se você não tiver certeza do seu número, esqueça essa regra e use nossa calculadora de raiz cúbica :-)

1. Primeiro, você precisa digitar o número para o qual precisa encontrar a raiz cúbica
2. Pressione √ (tecla raiz) duas vezes
3. Pressione x (sinal de multiplicação)
4. Pressione √ (tecla raiz) quatro vezes
5. Pressione x (sinal de multiplicação)
6. Pressione √ (tecla raiz) oito vezes
7. Pressione x (sinal de multiplicação)
8. Uma última vez, pressione a √ (tecla raiz) duas vezes
9. E agora você pode pressionar = (sinal de igual)! Aqui está a sua resposta!

Você ainda ficou com dúvidas? Verifique mais uma vez com outro exemplo!

Digamos que você precise fazer uma bola com um volume de 33,5 ml. Para prepará-la, você precisa conhecer seu raio. Como você provavelmente sabe, a equação para calcular o volume de uma esfera é a seguinte:

v = (4/3) ⋅ π ⋅ r³ `

Portanto, a equação para o raio é a seguinte:

r = ∛(3V/4π)

Você sabe que o volume é de 33,5 ml. Inicialmente, você precisa mudar para unidades de volume diferentes. A conversão mais simples é em cm³: 33,5 ml = 33,5 cm³. Agora você pode encontrar o raio:

r = ∛(100,5/12,56)

r = ∛(8)

r = 2

Para que uma bola tenha um volume de 33,5 ml, seu raio deve ser de 2 centímetros.

Com esta calculadora de raiz cúbica, você também pode calcular outras raízes. Basta escrever o número no campo Grau da raiz e você terá uma calculadora de raiz enésima. Nossa calculadora fará automaticamente todos os cálculos necessários, e você poderá usá-la livremente em seus cálculos!

Então, vamos pegar alguns exemplos. Vamos supor que você precise calcular a raiz quarta de 1296. Primeiro, você precisa escrever o número apropriado que deseja enraizar, ou seja, 1296. Em seguida, você deve alterar o grau da raiz para 4. E você tem o resultado! A raiz a quarta de 1296 é 6.

Nossa calculadora de raiz enésima também permite que você calcule a raiz de números irracionais. Vamos tentar calcular a π-ésima raiz. O símbolo π representa a razão entre a circunferência de um círculo e seu diâmetro. Seu valor é constante para cada círculo e é aproximadamente 3,14, mas você pode usar nossa calculadora de razão para encontrar seu valor com mais precisão!

Digamos que você queira calcular a raiz π-ésima de 450. Primeiro, escreva 450 no campo número. Em seguida, altere o grau da raiz, vamos arredondar e escrever 3,14 em vez de π. Agora você pode ver o resultado. É aproximadamente 7.

No final deste artigo, preparamos uma seção de matemática avançada para os mais persistentes. Você provavelmente sabe que os números positivos sempre têm duas raízes quadradas: uma negativa e outra positiva. Por exemplo, √4 = -2 e √4 = 2. Mas você sabia que uma regra semelhante se aplica às raízes cúbicas? Todos os números reais (exceto o zero) têm exatamente três raízes cúbicas: um número real e um par de números complexos. Os números complexos foram introduzidos pelos matemáticos há muito tempo para explicar problemas que os números reais não conseguem resolver. Geralmente, nós os expressamos da seguinte forma:

x = a + b⋅i

onde x é o número complexo com as partes real a e imaginária b (para números reais b = 0). O misterioso número imaginário i é definido como a raiz quadrada de -1:

i = √(-1)

Tudo bem, mas como esse conhecimento influencia o número de soluções de raiz cúbica? Como exemplo, considere as raízes cúbicas de 8, que são 2, -1 + i√3 e -1 - i√3. Se você não acredita, vamos verificar isso elevando-as à potência de 3, lembrando que i² = -1 e usando a fórmula (a + b)³ = a³ + 3a²b + 3ab² + b³:

1. 2³ = 8, o mais óbvio,
2. (-1 + i√3)³ = -1 + 3i√3 + 9 - 3i√3 = 8,
3. (-1 - i√3)³ = -1 - 3i√3 + 9 + 3i√3 = 8.

E agora, você se convenceu? Todos eles são iguais a 8!

A raiz cúbica de um produto de dois números é o produto das raízes cúbicas desses números. Ou seja, a fórmula é ∛(a ⋅ b) = ∛a ⋅ ∛b.

A resposta é -2/3. Para obter esse resultado, você deve seguir estas etapas:

1. Lembre-se da fórmula ∛(a / b) = ∛a / ∛b.
2. Calcule a raiz cúbica de -8. Claramente, ∛(-8) = -2.
3. Calcule a raiz cúbica de 27: temos ∛27 = 3.
4. O resultado final é -2/3. Bom trabalho!

O código Alt para o símbolo da raiz cúbica ∛ é 8731. Ou seja, para produzir ∛, você deve seguir as seguintes etapas:

1. Certifique-se de que o Num Lock esteja ativado.
2. Pressione uma das teclas Alt.
3. Mantendo pressionada a tecla Alt, digite o código 8731 usando o teclado numérico.
4. Solte a tecla Alt. Você verá o símbolo da raiz do cubo.
5. Método alternativo: copie o símbolo ∛ (Ctrl+C) e cole-o onde você precisar (Ctrl+V).