Calculadora de Vetores
Boas-vindas à calculadora de vetores da Omni! Ela ajudará você a realizar e entender uma série de operações vetoriais. Você tem as coordenadas cartesianas de dois vetores ou apenas sabe suas direções, sentidos e módulos? Talvez você precise encontrar o vetor que conecta dois pontos? Esta calculadora de vetores pode ser aplicada em todas essas situações. Ela executa:
- adição de vetores;
- subtração de vetores;
- multiplicação de vetores (produto vetorial e produto escalar!); e
- projeções de vetores.
Como bônus, também ensinaremos a você o que é a norma de um vetor e como normalizar um vetor.
Coordenadas cartesianas
Em um sistema de coordenadas xy retangular (também chamado cartesiano), descrevemos o vetor a em um plano bidimensional por suas coordenadas cartesianas:
a = [ax, ay].
Essas coordenadas correspondem ao processo de decompor o vetor a em um deslocamento horizontal ax ao longo do eixo x e em um deslocamento vertical ay ao longo do eixo y.
Da mesma forma, descrevemos os vetores no espaço tridimensional usando o sistema cartesiano xyz com três entradas:
a = [ax, ay, az],
que correspondem a deslocamentos ao longo dos eixos x, y e z, respectivamente.
Direção e módulo do vetor
Também podemos descrever um vetor plano em termos de sua direção e módulo. O módulo de um vetor é seu comprimento (também chamado de norma ou magnitude), e a direção de um vetor é o ângulo entre o eixo horizontal e o vetor.
Sejam [ax, ay] as coordenadas cartesianas de um vetor com módulo m e direção θ. Para converter um conjunto de coordenadas em outro, use as fórmulas a seguir:
ax = m × cos(θ)
ay = m × sen(θ)
Como determinar um vetor que conecta dois pontos?
Se você precisar determinar um vetor que conecta dois pontos, ou seja, a partir do ponto inicial e final, basta fazer a subtração das coordenadas destes pontos, ou seja:
-
Ponto inicial (origem): a = [ax, ay, az]
-
Ponto final: b = [bx, by, bz]
-
As coordenadas do vetor resultante entre esses dois pontos são:
[bx - ax, by - ay, bz - az]
Vamos dar uma olhada em um exemplo:
-
Ponto inicial:
[1, 2, 3] -
Ponto final:
[1, 1, -1] -
Coordenadas do vetor entre esses dois pontos:
[1 - 1, 1 - 2, 3 - (-1)] = [0, -1, 4]
Como normalizar um vetor? O que é a norma de um vetor?
A normalização de vetores é simplesmente apertar/esticar um vetor para que ele tenha módulo unitário, ou seja, igual a 1. Lembre-se de que a direção de um vetor deve ser mantida mesmo após a normalização!
Você pode encontrar a norma de um vetor aplicando o teorema de Pitágoras. A norma de um vetor é seu módulo, sendo este, a raiz quadrada da soma do quadrado de cada uma das coordenadas do seu vetor. A fim de normalizar, divida cada coordenada do vetor inicial pela norma. Você também pode usar a calculadora da norma de um vetor 🇺🇸 para determinar o módulo de qualquer vetor instantaneamente.
Exemplo:
Seja a = [2, 3, 4]. Vamos encontrar a norma de a:
|a| = √(4 + 9 + 16) = √29
A normalização de a nos dá o vetor a/|a| = [2/√29, 3√29, 4/√29]. Você sabia que temos uma ferramenta dedicada a esse tópico? Acesse a nossa calculadora de vetor unitário.
Como usar esta calculadora de vetores?
Para usar a calculadora de vetores, basta que você siga os passos abaixo:
- Informe se você está lidando com vetores planos (2D) ou espaciais (3D).
- Decida a operação vetorial que você deseja realizar. Você pode escolher adição ou subtração de vetores, multiplicação de vetores (produto escalar ou vetorial), normalização, projeção de vetores ou encontrar o vetor entre dois pontos.
- Insira seus dados. Você pode escolher entre coordenadas cartesianas ou direção e módulo do vetor (esta última opção no caso de vetores planos).
- A nossa calculadora de vetores retornará os resultados imediatamente 😊!
Adição de vetores
-
Em coordenadas cartesianas, podemos realizar a soma de vetores simplesmente somando as componentes correspondentes de cada vetor, ou seja:
para a = [ax, ay, az],
e b = [bx, by, bz],
temos a + b = [ax + bx, ay + by, az + bz].
Exemplo:
A soma de
a = [2, 3, 4]eb = [1, -2, 3]é:a + b = [2 + 1, 3 + (-2), 4 + 3] = [3, 1, 7] -
Método gráfico: para dois vetores
aeb, se você quiser obter a soma vetoriala + b, coloque a origem debna ponta da seta dea. O vetor resultante vai da origem deaaté a ponta da seta deb. Essa regra é conhecida como a lei do paralelogramo:
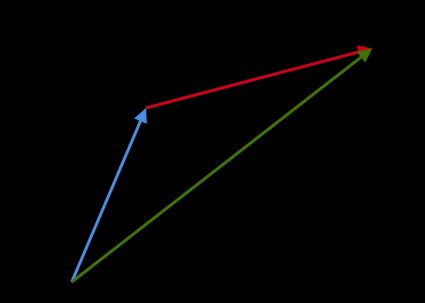
Subtração de vetores
A subtração envolvendo os vetores a e b pode ser entendida como a soma de a com -b. Para obter o vetor -b, reescreva as coordenadas do vetor b com sinais opostos, ou seja, troque os sinais positivos por negativos e os negativos por positivos:
assim, se b = [1, -2, 4],
então, -b = [-1, 2, -4]
-
Consequentemente, em coordenadas cartesianas, a subtração
a - bé realizada seguindo os passos abaixo:se a = [ax, ay, az]
e b = [bx, by, bz],
então, a - b = [ax - bx, ay - by, az - bz].
Exemplo:
A subtração de
a = [2, 3, 4]eb = [1, -2, 3]é dada pora - b = [2 - 1, 3 - (-2), 4 - 3] = [1, 5, 1]. -
Método gráfico: você obtém o vetor
a - bcolocando a ponta da seta debna ponta da seta deae desenhando um vetor que parte da origem deaaté a origem deb:
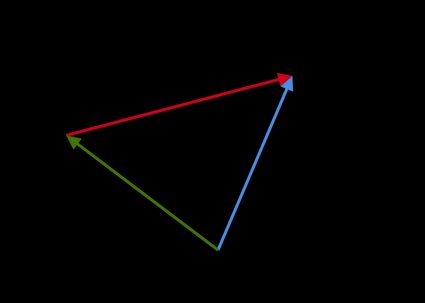
Multiplicação de vetores
Tenha cuidado quando quiser multiplicar vetores. Há vários tipos de produtos envolvendo vetores! Os mais populares são o produto vetorial e o produto escalar, que descrevemos a seguir:
Multiplicação de vetores - Produto vetorial
O produto vetorial é uma operação denotada pelo operador × envolvendo dois vetores e retornando outro vetor.
A fórmula é a seguinte:
a × b = |a| × |b| × sen(θ) × n,
onde:
θ: ângulo entreaeb;|a|e|b|: módulos deaeb; en: vetor unitário perpendicular aos vetoresaeb, determinado pela famosa Regra da Mão Direita.
Regra da mão direita:
Posicione a mão direita de modo que o dedo indicador aponte para o vetor
ae o dedo médio para o vetorb: o polegar mostra a direção do produto vetoriala × b.
- Interpretação gráfica: O vetor resultante
a × bforma um ângulo reto (perpendicular) em relação aos vetores iniciais e seu módulo é igual à área de um paralelogramo traçado a partir dos vetoresaeb:
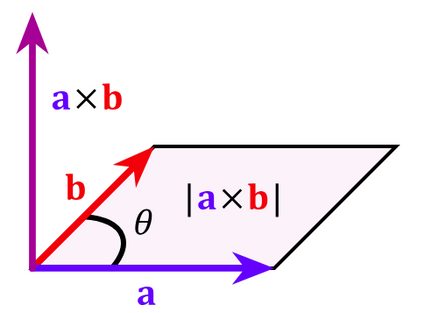
-
Considerando coordenadas cartesianas:
se a = [ax, ay, az],
e b = [bx, by, bz], temos
a × b = [ay×bz - az×by, az×bx - ax×bz, ax×by - ay×bx].
Exemplo:
O produto vetorial de
a = [2, 3, 4]eb = [1, -2, 3]é igual a`a × b = [3 × 3 - 4 × (-2), 4 × 1 - 2 × 3, 2 × (-2) - 3 × 1] = [17, -2, -7]`. -
Sim, a fórmula parece um pouco intimidadora. É mais fácil lembrar dela quando você percebe que as coordenadas do produto são equivalentes aos determinantes das matrizes 2 x 2 construídas a partir das componentes dos vetores iniciais:
- A primeira coordenada do vetor resultante é:

- A segunda coordenada do vetor resultante é:

- A terceira coordenada do vetor resultante é:

-
Tenha cuidado com a ordem dos vetores porque, ao contrário do produto escalar, a ordem importa para o produto vetorial! Mais precisamente, temos que
b × a = - a × b, portanto, se você errou na ordem, basta mudar o sinal e tudo ficará bem 🙃 -
O produto vetorial tem muitas aplicações em física e engenharia, por exemplo, você pode usá-lo para determinar a força de Lorentz agindo sobre partículas carregadas sujeitas a campos elétricos e magnéticos. Confira nossa calculadora de força de Lorentz 🇺🇸 e nossa calculadora de produto vetorial 🇺🇸 para ver outros exemplos!
-
O produto vetorial tem muitas aplicações em física e engenharia, por exemplo, você pode usá-lo para determinar a . Confira nossa para saber mais!
Multiplicação de vetores - Produto escalar
O produto escalar é uma operação denotada pelo operador · que envolve dois vetores e retorna um número (ou um escalar). Para dois vetores a e b, o produto escalar é o produto de seus módulos (normas) |a| e |b| pelo cosseno do ângulo θ entre eles, ou seja:
a · b = |a| × |b| × cos(θ).
-
Em coordenadas cartesianas, o produto escalar é a soma dos produtos das coordenadas correspondentes de seus dois vetores:
a · b = ax × bx + ay × by + az × bz
Exemplo:
O produto escalar de
a = [2, 3, 4]eb = [1, -2, 3]éa · b = 2 × 1 + 3 × (-2) + 4 × 3 = 2 - 6 + 12 = 8. -
Como você já deve ter concluído a partir da fórmula, a ordem não importa neste tipo de produto, assim:
a · b = b · a. -
Dica: calcular o produto escalar de um vetor com ele mesmo é equivalente ao quadrado do módulo (norma) do vetor:
a · a = |a|²! -
Para obter mais detalhes, consulte a calculadora de produto escalar 🇺🇸 da Omni.
Projeção vetorial
A projeção de b sobre a consiste em calcular a componente do vetor b paralela ao vetor a. Portanto, para encontrá-la, você só precisa determinar o fator de projeção escalar apropriado
-
Fórmula:
A projeção de
bsobreaé o vetoramultiplicado pelo fator:a · b / |a|².Exemplo:
Sejam
a = [2, 3, 4]eb = [1, -2, 3]. Vamos calcular a projeção debsobrea. Primeiro, vamos encontrar o fator de projeção escalar. Vimos anteriormente quea · b = 8e|a| = √29. Consequentemente, a projeção debsobreaé:8/29 · [2, 3, 4] = [16/29, 24/29, 32/29] -
Para encontrar a projeção de
bsobreagraficamente, você precisa decomporbao longo dos eixos paralelo e perpendicular aa. A componente paralela ao vetoraé a projeção debsobrea. Você também pode pensar nisso como a sombra que o vetorbprojetaria no vetorase houvesse uma fonte de luz acima destes vetores:
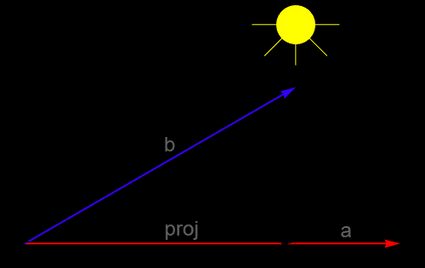
Para saber mais sobre a projeção de vetores, acesse a calculadora de projeção de um vetor 🇺🇸 da Omni.
Perguntas frequentes
O que é um vetor?
Um vetor é um objeto matemático definido por:
- Um módulo/magnitude; e
- Uma direção e um sentido.
Eles são substancialmente diferentes das quantidades escalares, uma vez que, escalares não mudam de valor com a direção.
Os vetores têm ampla aplicação na física, onde são usados para descrever posição e velocidade, por exemplo.
Como encontrar a projeção de um vetor sobre outro?
Se você considerar os vetores a e b, poderá encontrar a projeção de a sobre b seguindo os passos a seguir:
- Calcule o produto escalar entre
aeb:a · b. - Calcule o produto escalar de
bpor ele mesmo:b · b. - Faça a razão entre os dois resultados:
(a · b)/(b · b). - Multiplique o resultado (um escalar) pelo vetor
b:[(a · b)/(b · b)] × b.
O que é o produto escalar de dois vetores?
O produto escalar de dois vetores é uma operação que consiste em somar o produto de cada uma de suas componentes.
Se você tiver dois vetores, a = (a₁, a₂, a₃, ..., an) e b = (b₁, b₂, b₃, ..., bn), siga os passos a seguir para computar o produto escalar:
- Calcule o produto de cada par de componentes: a₁ × b₁, a × b₂, etc.
- Some os resultados: (a₁ × b₁) + (a₂ × b₂) + ....
Observe que você só pode calcular o produto escalar de vetores com o mesmo número de componentes.
Qual é a norma de um vetor com componentes (3,1,4,1,5)?
Para computar a norma, ou módulo, de um vetor com as componentes (3,1,4,1,5), aplique o teorema de Pitágoras generalizado sobre todas as componentes. Se o vetor for a = (a₁, a₂, a₃, ..., an), você encontrará a norma a partir da seguinte equação:
|a| = √(a₁² + a₂² + a₃² + ... + an²)
No caso do vetor (3,1,4,1,5), o módulo é:
√(3² + 1² + 4² + 1² + 5²) = √(9+1+16+1+25) = √(52) ≈ 7,21
