Calculadora da Razão de Ouro

A calculadora da razão de ouro da Omni permite determinar o comprimento das partes de um segmento que você precisa dividir para obter a proporção de ouro, também conhecida como proporção áurea. Antes de passarmos ao cálculo real da razão de ouro, vamos discutir o que ela significa. Nos tópicos abaixo, você encontrará todo o conhecimento que precisa!

Você também pode acessar a calculadora de proporção 🇺🇸 se quiser aprender sobre proporções em geral.

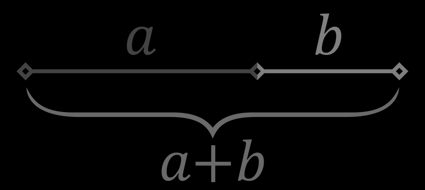
A razão de ouro (também conhecida como razão áurea ou proporção áurea) surge quando um segmento é dividido em duas partes, de modo que a razão entre a parte mais longa e a mais curta deve ser a mesma que a razão entre o segmento inteiro e a parte mais longa. Desta forma, se a parte mais longa tem comprimento $a$ e a parte mais curta tem comprimento $b$, a fórmula da razão de ouro é a seguinte:

Para calcular o valor da razão de ouro, você precisa resolver a equação acima e determinar a proporção $a/b$. Deste modo, é conveniente reescrever a equação como:

Assim, basta encontrarmos a solução $x$ da equação quadrática $x^2-x-1=0$. Ao realizarmos este cálculo por métodos bem conhecidos, descobrimos que a proporção áurea é igual a $\frac 12 (1+\sqrt{5})$, que é aproximadamente $1,61803398875...$. Esse número é frequentemente representado pela letra grega $\phi$.

Agora sabemos o que é a razão de ouro e como calcular seu valor, portanto, vamos verificar se dois comprimentos escolhidos satisfazem esta proporção divina.

Aqui estão as instruções passo a passo para ajudá-lo a descobrir se dois segmentos obedecem à razão de ouro:

1. Encontre o comprimento do segmento mais longo e identifique-o como a;
2. Encontre o comprimento do segmento mais curto e identifique-o como b;
3. Calcule a/b; e
4. Se a razão for (aproximadamente) igual a 1,618, seus segmentos estão em proporção áurea.

Você também pode usar a calculadora de razão de ouro da Omni para fazer o trabalho. Embora qualquer calculadora de razão possa ajudá-lo com isso, nossa calculadora de razão de ouro lida especificamente com essa questão, portanto, você não encontrará uma ferramenta melhor!

A calculadora de razão de ouro da Omni não poderia ser mais amigável e fácil de utilizar. Ela possui três campos, correspondentes aos três comprimentos que aparecem na fórmula da proporção áurea. Você só precisa inserir um deles para que os dois restantes sejam calculados automaticamente. Isso não é fantástico?

O retângulo de ouro (ou retângulo áureo), é um retângulo cujos comprimentos laterais obedecem à proporção áurea, ou seja, a proporção de seu comprimento em relação à largura é de $1,618$. Esse retângulo é frequentemente visto nas obras de arte, pois acredita-se que ele seja o mais agradável ao olho humano de todos os retângulos. A calculadora do retângulo de ouro é uma maneira conveniente de encontrar os lados de um retângulo áureo em vez de calculá-los à mão.

A razão de ouro possui uma relevância especial na ciência e na arte graças às suas propriedades e aparência. Do ponto de vista da matemática:

• Um retângulo de ouro pode ser dividido em dois retângulos áureos menores (ele mantém suas proporções); e
• A razão de ouro está profundamente correlacionada com o número 5. Esse número aparece em sua definição (φ = (1 + √5)/2) e no pentágono como a razão entre sua diagonal e um de seus lados.

Nas artes, a razão de ouro apareceu mais recentemente: Dalí, por exemplo, usou essa proporção em muitas de suas obras.

Muitas fontes históricas e contemporâneas afirmam que a razão de ouro é bastante onipresente na natureza. Alguns exemplos são:

• O padrão de crescimento das folhas;
• As superfícies geométricas de alguns vegetais e conchas; e
• As proporções dos ossos de alguns animais.

Entretanto, embora não possamos negar a presença de padrões geométricos na natureza, não podemos confirmar a exatidão das proporções dos exemplos acima: alguns apresentam grandes variações, enquanto outros são aproximações da razão de ouro.