30-60-90 Dreiecksrechner

Mit unserem 30-60-90-Dreiecksrechner kannst du alle relevanten Werte dieses speziellen rechtwinkligen Dreiecks finden. Egal, ob du nach den Formeln für die Hypotenuse des 30-60-90-Dreiecks suchst, die Seitenverhältnisse des 30-60-90-Dreiecks bestimmen willst oder einfach nur eine grafische Darstellung dieses Dreiecks brauchst, hier bist du definitiv auf der richtigen Seite. Lies weiter, um mehr über dieses bestimmte rechtwinklige Dreieck zu erfahren, oder sieh dir unser Tool für den Zwilling dieses Dreiecks an – den 45-45-90-Dreiecksrechner.

Wir sollten erst einmal klären, was „30 60 90“ überhaupt bedeutet. Wenn wir von einem 30-60-90-Dreieck sprechen, beziehen wir uns auf die Winkel des Dreiecks, welche gleich 30°, 60° und 90° sind.

Nehmen wir an, dass die kürzeste Seite (eine der zwei Katheten) eines 30-60-90-Dreiecks gleich a ist. Dann ist:

• die zweite Kathete gleich a√3,
• die Hypotenuse (die längste Seite) gleich 2a,
• die Fläche des Dreiecks gleich a²√3/2 und
• der Umfang gleich a(3 + √3).

Die 30-60-90-Dreiecksformeln sind ziemlich einfach, aber wie genau kommt man auf diese Ergebnisse? Sehen wir uns die Methoden an, mit denen wir diese Eigenschaften beweisen können:

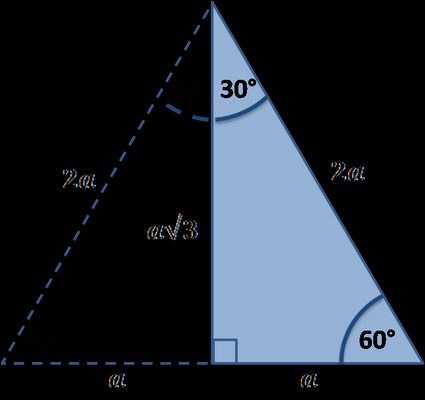
1. Indem wir die Eigenschaften des gleichseitigen Dreiecks nutzen

Ist dir aufgefallen, dass das 30-60-90-Dreieck einfach die Hälfte des gleichseitigen Dreiecks ist? Wenn du dich an die Formel für die Höhe eines solchen gleichmäßigen Dreiecks erinnerst, dann kennst du bereits die Länge der zweiten Kathete. Diese ergibt sich aus der Multiplikation der Seitenlänge mit der Quadratwurzel aus 3 und Division durch 2:

h = c√3/2, h = b und c = 2a also b = c√3/2 = a√3

2. Mittels trigonometrischen Funktionen

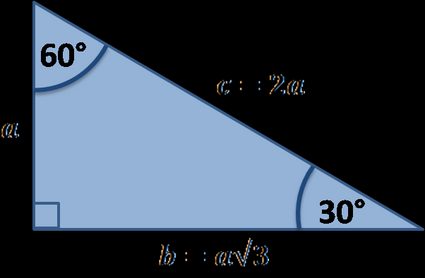
Wenn du mit den Grundlagen der Trigonometrie vertraut bist, kannst du z. B. den Sinus und Kosinus von 30° verwenden, um die anderen Seitenlängen zu ermitteln:

a/c = sin(30°) = 1/2 also c = 2a

b/c = sin(60°) = √3/2 also b = c√3/2 = a√3

Wenn du die Länge zweier Dreiecksseiten bereits kennst, kannst du die dritte mithilfe des Satzes des Pythagoras ermitteln. Die oben beschriebenen Methoden sind jedoch praktischer, da sie nur die Länge einer der 30-60-90-Dreiecksseiten benötigen.

Wenn wir die kürzere Kathete a kennen, können wir Folgendes herleiten:

• b = a√3

• c = 2a

Falls jedoch b, also die längere Kathete, angegeben ist:

• a = b√3/3

• c = 2b√3/3

Wenn die Hypotenuse c bekannt ist, sehen die anderen Längen wie folgt aus:

• a = c/2

• b = c√3/2

Alternativ kannst du einfach deine Werte in den 30-60-90-Dreiecksrechner eingeben, er erledigt den Rest!

Die wichtigste Eigenschaft dieses spezifischen Dreiecks ist, dass er einen rechten Winkel besitzt und seine Seiten stets in dem folgenden Verhältnis zueinander stehen a : a√3 : 2a. Ist doch leicht zu merken! Eine ungewöhnliche Eigenschaft dieses 30-60-90-Dreiecks ist zudem, dass es das einzige rechtwinklige Dreieck ist, dessen Winkel aus einer arithmetischen Folge besteht.

Was ist eine arithmetische Folge? Schau dir unseren arithmetische Folge Rechner an, um mehr zu erfahren!

In einem 30-60-90-Dreieck können folgende Verhältnisse vorkommen:

• 1 : 2 : 3 für Winkel von (30° : 60° : 90°) und
• 1 : √3 : 2 für die Seiten (a : a√3 : 2a).

Da du bereits die Eigenschaften eines 30-60-90-Dreiecks kennst, ist es höchste Zeit, dein Wissen in der Praxis anzuwenden!

1. Gebe den vorgegebenen Wert in den Rechner ein. Nehmen wir an, wir wollen die Werte für das rote 30-60-90-Dreieck auf dem Bild berechnen und dass die Länge der Seite 11 cm beträgt.
2. Nun erscheinen alle anderen Werte! Dank dieses 30-60-90-Dreiecksrechners weißt du, dass:

• Die kürzere Kathete 6,35 cm lang ist – denn a = b√3/3 = 11 cm ∙ √3/3 ≈ 6,35 cm.
• Die Hypotenuse 12,7 cm lang ist – weil c = 2b√3/3 = 2a ≈ 12,7 cm.
• Die Fläche gleich 34,9 cm² ist – dies ergibt sich aus der Multiplikation der Kathetenlängen und der Division durch 2 Fläche = (a²√3)/2 ≈ 34,9 cm².
• Der Umfang beträgt 30,05 cm – wenn du alle Seiten addierst, erhältst du das Ergebnis Umfang = a + a√3 + 2a = a(3 + √3) ≈ 30,05 cm.