45 45 90 Dreieck Rechner

Unser 45-45-90-Dreieck-Rechner setzt sich genau mit dieser Art von rechtwinkligen Dreiecken auseinander. Finde heraus, wie man die Seiten, die Hypotenuse, die Fläche und den Umfang eines solchen Dreiecks mit 45 Grad berechnet und lerne die für ein 45-45-90-Dreieck typische Verhältnisse und Formeln kennen. Außerdem besprechen wir die Regeln, die für diese Dreiecke gelten und höchstwahrscheinlich in deinen Hausaufgaben vorkommen werden. Du wirst dich nie wieder fragen müssen, wie du die Werte eines 45-45-90-Dreiecks bestimmst und den 90 Grad-Winkel berechnest!

Wenn du mehr über andere typische rechtwinklige Dreiecke und die Berechnung von Dreiecken mit 90 Grad-Winkeln wissen möchtest, schau dir den 30-60-90 Dreiecksrechner und den Rechner für spezielle rechtwinklige Dreiecke an.

Suchst du die Formeln für das 45-45-90-Dreieck? Dann bist du hier beim 45-45-90-Dreieck-Rechner genau richtig! Finde heraus, wie ein Dreieck mit 90 Grad-Winkel berechnet wird. Wenn eine der Katheten des Dreiecks gleich a ist, dann ist:

• die zweite Kathete ebenso gleich a,
• die Hypotenuse (die längste Seite) gleich a√2,
• die Fläche gleich a²/2 und
• der Umfang gleich a(2 + √2).

OK, diese Formeln für die Dreiecksberechnung mit 90 Grad sehen einfach aus, aber wie kann man sie herleiten? Es gibt einige Methoden, um sie zu beweisen. Die bekanntesten davon sind:

1. Mittels des Satzes des Pythagoras

• Da du die Länge der Kathete a kennst, kennst du auch die Länge der anderen, da beide gleich lang sind.

• Finde die Hypotenuse mithilfe des Satzes des Pythagoras: Wir wissen, dass a² + b² = c² und a = b sind, somit kommen wir auf

  a² + a² = c²

  was

  c = √(2a²) = a√2 ergibt

2. Indem wir uns die Quadrateigenschaften zunutze machen

Hast du bemerkt, dass das 45-45-90-Dreieck die Hälfte eines Quadrats ist, das entlang seiner Diagonale geschnitten wurde?

• Auch hier wissen wir, dass beide Katheten gleich a sind.
• Wie du dich wahrscheinlich erinnerst, ist die Diagonale des Quadrats gleich der Seite mal der Quadratwurzel aus 2, also a√2. In unserem Fall ist diese Diagonale gleich der Hypotenuse. Das ging aber schnell!

3. Durch die Trigonometrie

Wenn du dich mit der Trigonometrie auskennst, kannst du die Eigenschaften des Sinus und Kosinus nutzen. Um dieses spezielle Dreieck mit 45 Grad zu berechnen, sind beide gleich √2/2. Also:
a/c = √2/2 sodass c = a√2 ist

Um die Fläche des Dreiecks zu bestimmen, benutze die bekannte Flächenformel für Dreiecke: Fläche = Grundseite x Höhe / 2. In unserem Fall ist eine der Katheten die Basis und die andere die Höhe, da es zwischen ihnen ein rechter Winkel liegt. Die Fläche dieses Dreiecks mit 90 Grad-Winkel ist also:

Fläche = a² / 2

Um den Umfang des Dreiecks mit 45 Grad zu berechnen, addierst du einfach alle Seitenlängen:

Umfang = a + b + c = a + a + a√2 = a(2 + √2)

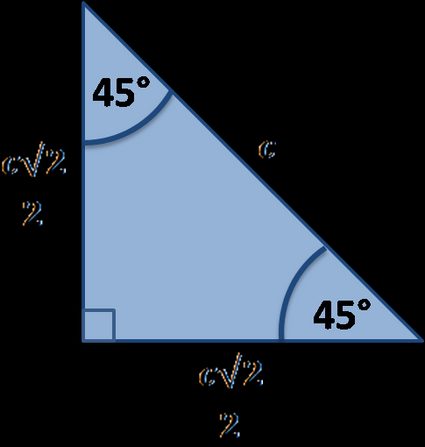
Die Katheten eines solchen Dreiecks sind gleich lang; die Hypotenuse wird direkt aus der Gleichung c = a√2 berechnet. Wenn die Länge der Hypotenuse gegeben ist, ist die Seitenlänge gleich a = c√2/2.

Die wichtigste Regel ist, dass dieses spezielle Dreieck einen rechten Winkel besitzt und die anderen zwei Winkel 45°-Grad-Winkel sind. Das bedeutet, dass zwei der Seiten – die Katheten – gleich lang sind, womit du die Hypotenuse leicht berechnen kannst. Weitere interessante Eigenschaften des 45-45-90-Dreiecks sind:

• Dass es das einzige rechtwinklige Dreieck ist, das zugleich ein gleichschenkliges Dreieck ist.
• Von allen rechtwinkligen Dreiecken hat es das kleinste Verhältnis von Hypotenuse zur Summe der Seitenlängen.
• Von allen rechtwinkligen Dreiecken hat es das größte Höhenverhältnis von der Hypotenuse zur Summe der Seitenlängen.

In einem 45-45-90-Dreieck kommen die folgenden Verhältnisse vor:

• 1 : 1 : 2 für die Winkel (45° : 45° : 90°) und
• 1 : 1 : √2 für die Seiten (a : a : a√2).

Sieh dir dieses praktische Beispiel an, um die Dreiecksberechnung mit 90 Grad besser zu verstehen.

Angenommen, wir möchten die die Dreiecksberechnung mit 90 Grad für ein gleichschenkliges Dreiecks durchführen.

1. Tippe den angegebenen Wert ein. Nehmen wir an, dass die Schenkel 9 cm lang sind. Gib diesen Wert in das Feld a oder b ein.
2. Der 45-45-90-Dreieck-Rechner zeigt dir die restlichen Werte an. Jetzt kennst du:

• die Hypotenusenlänge – 9 cm ∙ √2 = 12,73 cm,
• die Fläche – 9 cm ∙ 9 cm / 2 = 40,5 cm² und
• den Umfang – 9 cm + 9 cm + 9 cm ∙ √2 = 30,73 cm.

Vergiss nicht, dass du die Einheiten ändern kannst, indem du auf die angegebene Einheit im Rechner klickst. Denk auch dran, dass unser 45-45-90-Dreieck-Rechner ein flexibles Werkzeug ist – wenn du nur die Fläche, die Hypotenuse oder sogar nur den Umfang kennst, kann er auch die restlichen Werte berechnen. Wahnsinn!