Kosinussatz Rechner

Der Kosinussatz-Rechner kann dir helfen, eine Vielzahl von Dreiecksaufgaben zu lösen. Du erfährst, was der Kosinussatz ist, die Kosinusformel und ihre Anwendungen. Scrolle nach unten, um herauszufinden, wann und wie du den Kosinussatz anwenden kannst, und sieh dir die Beweise für dieses Gesetz an. Dank dieses Dreiecksrechners kannst du die Eigenschaften jedes beliebigen Dreiecks schnell ermitteln.

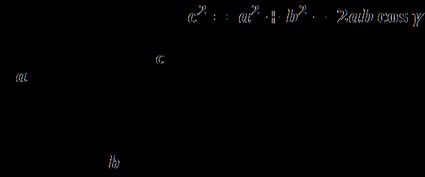
Wenn du dich eigentlich fragst, was ein Kosinus ist, solltest du dir unseren Kosinus Rechner 🇺🇸 ansehen.

Der Kosinussatz besagt, dass für ein Dreieck, dessen Seiten und Winkel mit den oben abgebildeten Symbolen gekennzeichnet sind, die folgenden Regeln gelten:

a² = b² + c² - 2bc ∙ cos(α)

b² = a² + c² - 2ac ∙ cos(β)

c² = a² + b² - 2ab ∙ cos(γ)

Bei einem rechtwinkligen Dreieck ist der Winkel Gamma (γ), also der Winkel zwischen den Schenkeln a und b, gleich 90°. Da der Kosinus von 90° = 0 ist, lässt sich die Formel des Kosinussatzes in diesem speziellen Fall auf die bekannte Gleichung des Satzes des Pythagoras reduzieren:

a² = b² + c² - 2bc ∙ cos(90°)

a² = b² + c²

Der Kosinussatz beschreibt das Verhältnis zwischen den Seitenlängen eines Dreiecks und dem Kosinus seiner Winkel. Es kann auf alle Dreiecke angewendet werden, nicht nur auf rechtwinklige Dreiecke. Dieses Gesetz ist eine Verallgemeinerung des Satzes des Pythagoras, da es dir erlaubt, die Länge einer der Seiten zu berechnen, wenn du die Länge der beiden anderen Seiten und den von ihnen eingeschlossenen Winkel kennst.

Das Gesetz erschien in Euklids Element, einer mathematischen Abhandlung, die Definitionen, Postulate und Lehrsätze der Geometrie enthält. Euklid formulierte es nicht so, wie wir es heute lernen, denn das Konzept des Kosinus war noch nicht entwickelt worden.

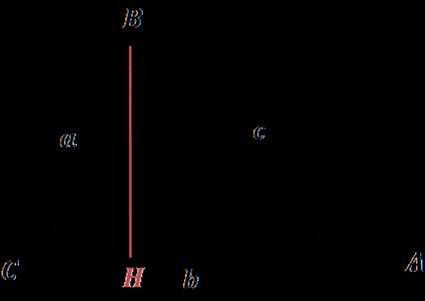
AB² = CA² + CB² - 2 ∙ CA ∙ CH (für spitze Winkel)

AB² = CA² + CB² - 2 ∙ CA ∙ CH (für stumpfe Winkel)

Wir können den Satz von Euklid jedoch leicht in die aktuelle Form der Kosinusformel umformulieren:

CH = CB ∙ cos(γ), also AB² = CA² + CB² - 2 ∙ CA ∙ (CB ∙ cos(γ)).

Wenn wir die Schreibweise ändern, erhalten wir den bekannten Ausdruck:

c² = a² + b² - 2ab ∙ cos(γ).

Die erste explizite Gleichung des Kosinussatzes wurde im 15. Jahrhundert von dem persischen Mathematiker d'Al-Kashi aufgestellt. Im 16. Jahrhundert wurde das Gesetz von dem berühmten französischen Mathematiker Viète popularisiert, bevor es im 19. Jahrhundert seine endgültige Form annahm.

Du kannst diese Formeln des Kosinussatzes umwandeln, um einige Probleme bei Dreiecksberechnungen zu lösen. Du kannst sie zur Lösung folgender Parameter verwenden:

1. Die dritte Seite eines Dreiecks, wenn du zwei Seiten und den Winkel zwischen ihnen kennst (SAS):

   • a = √[b² + c² - 2bc ∙ cos(α)]

   • b = √[a² + c² - 2ac ∙ cos(β)]

   • c = √[a² + b² - 2ab ∙ cos(γ)]

2. Die Winkel eines Dreiecks, wenn du alle drei Seiten kennst (SSS):

   • α = arccos [(b² + c² - a²)/(2bc)]

   • β = arccos [(a² + c² - b²)/(2ac)]α = arccos [(a² + c² - b²)/(2ac)

   • γ = arccos [(a² + b² - c²)/(2ab)]

3. Die dritte Seite eines Dreiecks, wenn du zwei Seiten und einen Winkel kennst, der einer der beiden gegenüberliegt (SSW):

   • a = b ∙ cos(γ) ± √[c² - b² × sin²(γ)]

   • b = c ∙ cos(α) ± √[a² - c² × sin²(α)]

   • c = a ∙ cos(β) ± √[b² - a² × sin²(β)]

Denke daran, dass die Kenntnis von zwei Seiten und einem angrenzenden Winkel zwei verschiedene mögliche Dreiecke ergeben kann (oder eine oder null positive Lösungen, abhängig von den gegebenen Daten). Deshalb haben wir uns entschieden, SSW und SSS in dieses Tool zu integrieren, aber nicht SWS.

Der Kosinussatz ist eines der grundlegenden Gesetze und wird für viele geometrische Probleme verwendet. Wir nutzen dieses Gesetz auch in vielen Omnitools, um nur ein paar zu nennen:

• Dreieckswinkel Rechner
• Fläche Dreieck Rechner
• Umfang Dreieck Rechner 🇺🇸
• Dreiecksprisma Rechner

Du kannst den Kosinussatz-Rechner auch mit dem Sinussatz Rechner kombinieren, um andere Probleme zu lösen, z. B. um die Seite des Dreiecks zu finden, wenn zwei Winkel und eine Seite (WWS und WSW) gegeben sind.

Es gibt viele Möglichkeiten, den Kosinussatz zu beweisen. Eine davon hast du bereits kennengelernt – sie stammt direkt aus Euklids Formulierung des Gesetzes und einer Anwendung des Satzes des Pythagoras. Die anderen Beweise für den Kosinussatz sind folgende:

1. Trigonometrie

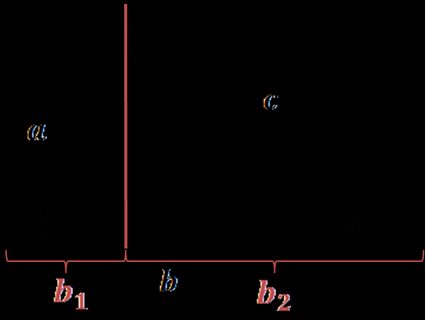
Zeichne eine Gerade für die Höhe des Dreiecks und teile die Seite, die senkrecht dazu steht, in zwei Teile:

b = b₁ + b₂.

Aus den Definitionen von Sinus und Kosinus kann b₁ als a ∙ cos(γ) und b₂ = c ∙ cos(α) ausgedrückt werden. Daraus folgt:

b = a ∙ cos(γ) + c ∙ cos(α) und durch Multiplikation mit b erhalten wir:

b² = ab ∙ cos(γ) + bc ∙ cos(α) (1).

Für die anderen beiden Seiten lassen sich analoge Gleichungen ableiten:

a² = ac ∙ cos(β) + ab ∙ cos(γ) (2); und

c² = bc ∙ cos(α) + ac ∙ cos(β) (3).

Um den Beweis des Kosinussatzes abzuschließen, musst du die Gleichungen (1) und (2) addieren und (3) subtrahieren:

a² + b² - c² = ac ∙ cos(β) + ab ∙ cos(γ) + bc ∙ cos(α) + ab ∙ cos(γ) - bc ∙ cos(α) - ac ∙ cos(β).

Das Vereinfachung der Gleichung ergibt eine der Formen der Kosinusregel:

a² + b² - c² = 2ab ∙ cos(γ);

c² = a² + b² - 2ab ∙ cos(γ).

Wenn du die Reihenfolge änderst, in der sie addiert und subtrahiert werden, kannst du die anderen Formeln des Kosinussatzes ableiten.

2. Formel für die Entfernung

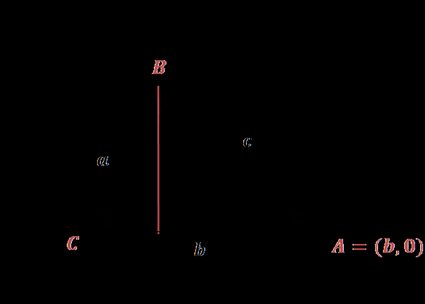
Nehmen wir, wie auf der obigen Abbildung, an, dass: C = (0,0) und A = (b,0) sind.

Um die Koordinaten von B zu finden, können wir die Definition vom Sinus und Kosinus verwenden:

B = (a ∙ cos(γ), a ∙ sin(γ))

Aus der Entfernungsformel können wir ablesen:

c = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(a ∙ cos(γ) - b)² + (a ∙ sin(γ) - 0)²]

Daraus folgt:

c² = a² ∙ cos(γ)² - 2ab ∙ cos(γ) + b² + a² ∙ sin(γ)²

c² = b² + a²(sin(γ)² + cos(γ)²) - 2ab ∙ cos(γ)

Da die Summe der Quadrate von Sinus und Kosinus gleich 1 ist, erhalten wir die endgültige Formel:

c² = a² + b² - 2ab × cos(γ).

3. Satz von Ptolemäus

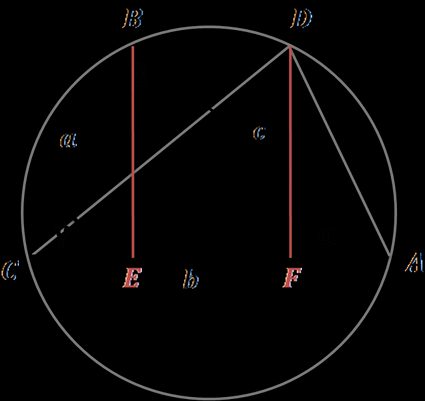
Ein anderer Beweis für den Kosinussatz, der relativ leicht zu verstehen ist, verwendet den Satz von Ptolemäus:

• Angenommen, wir haben das Dreieck ABC, wie in der obigen Abbildung zu sehen, in seinem Umkreis gezeichnet.

• Konstruiere das kongruente Dreieck ADC, wobei AD = BC und DC = BA

• Die Höhen der Punkte B und D teilen die Basis AC durch E bzw. F. CE ist gleich FA.

• Aus der Definition des Kosinus können wir CE als a ∙ cos(γ) ausdrücken.

• Somit schreiben wir für BD = EF = AC - 2 ∙ CE = b - 2 ∙ a ∙ cos(γ).

• Dann können wir für unser Viereck ADBC den Satz von Ptolemäus anwenden, der die Beziehung zwischen den vier Seiten und den beiden Diagonalen erklärt. Der Satz besagt, dass bei zyklischen Vierecken die Summe der Produkte der gegenüberliegenden Seiten gleich dem Produkt der beiden Diagonalen ist:

  BC ∙ DA + CA ∙ BD = AB ∙ CD,

  also in unserem Fall:

  a² + b ∙ (b - 2 ∙ a ∙ cos(γ)) + a² = c².

• Nach dem Kürzen erhalten wir die endgültige Formel:

  c² = a² + b² - 2ab ∙ cos(γ).

Der große Vorteil dieser drei Beweise ist ihre Universalität – sie funktionieren für spitze, rechteckige und stumpfe Dreiecke.

4. Anwendung des Sinussatzes;
5. Anwendung der Definition des Skalarprodukts 🇺🇸;
6. Vergleich von Flächeninhalten; und
7. Geometrie des Kreises.

Die letzten beiden Beweise erfordern die Unterscheidung zwischen verschiedenen Dreiecksfällen. Der Beweis, der auf der Definition des Skalarprodukts beruht, wird in einem anderen Artikel gezeigt, und der Beweis mit dem Sinussatz ist ziemlich kompliziert, weshalb wir ihn hier nicht wiedergeben. Wenn du neugierig auf diese Beweise zum Kosinusgesetz bist, schau dir die Wikipedia Erklärung (englisch) an.

1. Fange damit an, dein Problem zu formulieren. Du kennst zum Beispiel zwei Seiten des Dreiecks und den Winkel zwischen ihnen und suchst die verbleibende Seite.

2. Gib die bekannten Werte in die entsprechenden Felder dieses Rechners ein. Vergiss nicht, anhand der Abbildung oben zu überprüfen, ob du die Seiten und Winkel mit den richtigen Symbolen bezeichnet hast.

3. Sieh zu, wie unser Kosinussatz Rechner alle Berechnungen für dich durchführt!

Wenn deine Aufgabe darin besteht, die Winkel eines Dreiecks mit allen drei Seiten zu bestimmen, brauchst du nur die Formeln der umgewandelten Kosinusregel zu verwenden:

α = arccos [(b² + c² - a²)/(2bc)]
β = arccos [(a² + c² - b²)/(2ac)]
γ = arccos [(a² + b² - c²)/(2ab)]

Lass uns einen der Winkel berechnen. Nehmen wir an, dass a = 4 cm, b = 5 cm und c = 6 cm ist. Wir verwenden die erste Gleichung, um α zu finden:

α = arccos [(b² + c² - a²)/(2bc)]

= arccos [(5² + 6² - 4²)/(2 ∙ 5 ∙ 6)]

= arccos [(25 + 36 - 16)/60]

= arccos [(45/60)] = arccos [0,75]

α = 41,41°

Den zweiten Winkel kannst du auf analoge Weise aus der zweiten Gleichung berechnen, und den dritten Winkel kannst du ermitteln, indem du weißt, dass die Summe der Winkel in einem Dreieck gleich 180° (π) ist.

Wenn du etwas Zeit sparen möchtest, gib die Seitenlängen in unseren Kosinussatz-Rechner ein – unser Tool ist eine sichere Sache! Befolge einfach diese einfachen Schritte:

1. Wähle die Option, die von den gegebenen Werten abhängt. Wir müssen die zweite Option wählen – SSS (3 Seiten).

2. Gib die bekannten Werte ein. Gib die Seiten ein: a = 4 cm, b = 5 cm und c = 6 cm.

3. Der Rechner zeigt das Ergebnis an! In unserem Fall sind die Winkel gleich: α = 41,41°, β = 55,77° und γ = 82,82°.

Nach dieser Erklärung sind wir uns sicher, dass du verstanden hast, was der Kosinussatz ist und wann du ihn anwendest. Probiere dieses Tool aus, löse einige Aufgaben und denke daran, dass Übung den Meister macht!