Kubikwurzel Rechner

Unser Kubikwurzel-Rechner ist ein praktisches Tool, mit dem du die Kubikwurzel, auch 3. Wurzel genannt, einer beliebigen positiven Zahl bestimmen kannst. Du kannst unseren Rechner sofort benutzen; gib einfach die Zahl ein, aus der du die Kubikwurzel ziehen möchtest, und schon bist du fertig! Du kannst die Berechnungen auch andersherum durchführen und eine Zahl mit 3 exponenzieren. Gib diese Zahl dafür einfach in das letzte Feld ein! Das kann bei der Suche nach sogenannten perfekten Kubikzahlen 🇺🇸 sehr nützlich sein. Mehr darüber erfährst du im folgenden Artikel.

Dank unseres Kubikwurzel-Rechners kannst du auch die Wurzeln anderer Grade berechnen. Dazu musst du die Zahl im Feld Grad der Wurzel ändern. Wenn du mehr über die Definition der Kubikwurzel erfahren, dich mit den Eigenschaften der Kubikwurzelfunktion vertraut machen und eine Liste der perfekten Kubikzahlen finden möchtest, empfehlen wir dir dringend, diesen Text weiterzulesen. Darin findest du auch einige Tricks, wie du die Kubikwurzel auf einem Taschenrechner findest oder wie du sie im Kopf berechnen kannst.

Wenn du dich für die Geschichte der Quadratwurzel-Symbole interessierst, schau dir den Quadratwurzel Rechner an, in dem wir sie diskutieren.

Nehmen wir an, du möchtest die Kubikwurzel einer Zahl, x, finden. Die Kubikwurzel, y, ist eine solche Zahl, die, wenn man sie mit 3 exponenziert, x als Ergebnis liefert, was in dieser Formel dargestellt wird:

∛x = y ⟺ y^3 = x,

wobei ⟺ ein mathematisches Symbol ist, das wenn und nur wenn bedeutet.

Es ist auch möglich, die Kubikwurzel anders zu notieren, was manchmal viel bequemer ist. Das liegt daran, dass die Kubikwurzel ein Sonderfall des Exponenten ist. Sie kann also folgendermaßen beschrieben werden:

∛(x) = x^(1/3).

Ein geometrisches Beispiel kann dir helfen, dies zu verstehen. Das beste Beispiel, das wir geben können, ist der Würfel. Die Kubikwurzel aus dem Volumen eines Würfels ist seine Kantenlänge. Wenn ein Würfel also zum Beispiel ein Volumen von 27 cm³ hat, dann ist die Länge seiner Kanten gleich der Kubikwurzel aus 27 cm³, also 3 cm. Einfach?

Du solltest bedenken, dass die Kubikwurzel in den meisten Fällen keine rationale Zahl sein wird. Diese Zahlen können als Quotient zweier natürlicher Zahlen ausgedrückt werden, also als Bruch. Brüche können einige Schwierigkeiten verursachen, vor allem wenn es darum geht, sie zu addieren. Wenn du Probleme mit Brüchen hast, hilft dir unser Brüche Addieren Rechner 🇺🇸 weiter.

Mit unserem Kubikwurzel-Rechner ist es ganz einfach, die Kubikwurzel einer beliebigen positiven Zahl zu finden! Gib einfach eine beliebige Zahl ein, um ihre Kubikwurzel zu finden. Die Kubikwurzel von 216 ist zum Beispiel 6. Die Liste der perfekten Kubikzahlen findest du im nächsten Abschnitt.

Beachte, dass es auch möglich ist, eine Kubikwurzel aus einer negativen Zahl zu finden. Schließlich ist eine negative Zahl, mit 3 exponenziert, immer noch negativ – zum Beispiel (-6)³ = -216.

Du musst aber bedenken, dass jede Zahl, die nicht Null ist, drei Kubikwurzeln hat: mindestens eine reelle und zwei imaginäre. Dieser Kubikwurzel-Rechner befasst sich nur mit reellen Zahlen, aber wenn du dich dafür interessierst, empfehlen wir dir, mehr zum Thema imaginärer Zahlen zu lesen!

Die häufigsten Kubikwurzel-Werte findest du unten. Diese Zahlen werden auch oft perfekte Kubikzahlen genannt, da ihre Kubikwurzeln ganze Zahlen sind. Hier ist die Liste der zehn ersten perfekten Kubikzahlen:

• Kubikwurzel von 1: ∛1 = 1, denn 1 ∙ 1 ∙ 1 = 1;
• Kubikwurzel von 8: ∛8 = 2, denn 2 ∙ 2 ∙ 2 = 8;
• Kubikwurzel von 27: ∛27 = 3, denn 3 ∙ 3 ∙ 3 = 27;
• Kubikwurzel von 64: ∛64 = 4, denn 4 ∙ 4 ∙ 4 = 64;
• Kubikwurzel von 125: ∛125 = 5, da 5 ∙ 5 ∙ 5 = 125;
• Kubikwurzel aus 216: ∛216 = 6, da 6 ∙ 6 ∙ 6 = 216;
• Kubikwurzel von 343: ∛343 = 7, da 7 ∙ 7 ∙ 7 = 343;
• Kubikwurzel von 512: ∛512 = 8, da 8 ∙ 8 ∙ 8 = 512;
• Kubikwurzel von 729: ∛729 = 9, denn 9 ∙ 9 ∙ 9 = 729; und
• Kubikwurzel von 1000: ∛1000 = 10, da 10 ∙ 10 ∙ 10 = 1000.

Wie du siehst, wachsen die Zahlen ziemlich schnell, aber manchmal musst du mit noch größeren Zahlen umgehen, z. B. mit Faktorzahlen. In diesem Fall empfehlen wir dir, die wissenschaftliche Notation zu verwenden, mit der du wirklich große oder kleine Zahlen viel bequemer aufschreiben kannst.

Die meisten anderen Zahlen sind zwar keine perfekten Kubikzahlen, aber einige von ihnen werden trotzdem häufig verwendet. Hier ist eine Liste mit einigen der nicht perfekten Kubikzahlen auf Hundertstel gerundet:

• Kubikwurzel von 2: ∛2 ≈ 1,26;
• Kubikwurzel von 3: ∛3 ≈ 1,44;
• Kubikwurzel von 4: ∛4 ≈ 1,59;
• Kubikwurzel von 5: ∛5 ≈ 1,71; und
• Kubikwurzel von 10: ∛10 ≈ 2,15.

Zögere nicht, unseren Kubikwurzel-Rechner zu benutzen, wenn die Zahl, die du brauchst, nicht in dieser Liste steht!

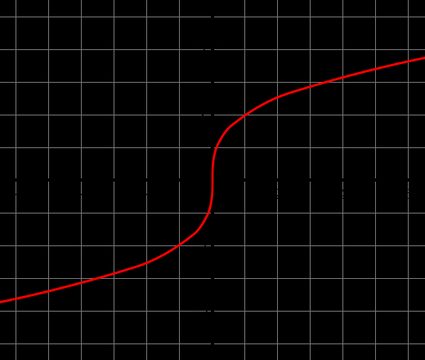
Du kannst die Funktion y = ∛(x) grafisch darstellen. Anders als z. B. die Logarithmusfunktion ist die Kubikwurzelfunktion eine ungerade Funktion – das bedeutet, dass sie symmetrisch zum Ursprung ist und die Bedingung - f(x) = f(-x) erfüllt. Auch diese Funktion geht durch null.

Mithilfe dieser Funktion kannst du einen Graphen der Kubikwurzel zeichnen, der unten abgebildet ist. Wir empfehlen dir auch den ABC-Formel Rechner 🇺🇸, um dir andere Funktionsformeln anzuschauen!

Glaubst du, dass es möglich ist, einfache Aufgaben mit Kubikwurzeln ohne einen Online-Rechner oder sogar ohne Bleistift und Papier zu lösen? Wenn du denkst, dass es unmöglich ist oder dass du es nicht kannst, dann schau dir diese Methode an, denn sie ist sehr einfach. Allerdings funktioniert sie nur für perfekte Kubikzahlen. Vergiss alle Regeln aus Rechenbüchern und betrachte für einen Moment die folgende, von Robert Kelly beschriebene Methode.

Zunächst einmal ist es wichtig, sich die Kubikwerte der Zahlen von 1 bis 10 und die letzte Ziffer ihres Kubiks einzuprägen. Sie sind in der folgenden Tabelle aufgeführt.

Wenn du die Kubikwurzel einer Zahl wissen möchtest, schau dir zuerst die Tausender an (lass die letzten drei Ziffern weg). Zum Beispiel für die Zahl 185 193: Die Tausender sind 185. Das Kubik von 5 ist 125 und das von 6 ist 216. Es ist also offensichtlich, dass die gesuchte Zahl zwischen 50 und 60 liegt. Der nächste Schritt besteht darin, alle anderen Zahlen außer der letzten Ziffer zu ignorieren. Wir sehen, dass es die 3 ist, also überprüfe dein Gedächtnis oder unsere Tabelle. Du wirst feststellen, dass die Zahl, die du suchst, 7 ist. Die Antwort lautet also 57! Einfach?

Nehmen wir ein anderes Beispiel und machen es Schritt für Schritt!

1. Stell dir die Zahl, die du wissen möchtest, als Kubikwurzel vor. Nehmen wir 17 576.
2. Lass die drei letzten Ziffern weg.
3. Finde die zwei nächstgelegenen Kubikwurzeln, die du kennst. Die Kubikwurzel von 8 ist 2, und die Kubikwurzel von 27 ist 3. Deine Zahl liegt also zwischen 20 und 30.
4. Schau dir die letzte Ziffer an. Die letzte Ziffer von 17 576 ist 6.
5. Schau auf unsere Tabelle: Die letzte Ziffer 6 entspricht der Zahl 6. Dies ist die letzte Ziffer deiner Zahl.
6. Kombiniere die beiden: 26. Das ist die Kubikwurzel von 17 576!

Wir erinnern dich daran, dass dieser Algorithmus nur bei perfekten Kubikzahlen funktioniert! Und die Wahrscheinlichkeit, dass eine Zufallszahl ein perfektes Kubik ist, ist leider sehr gering. Du hast nur eine Chance von 0,0091 Prozent, eine Zahl zwischen 1000 und 1 000 000 zu finden. Wenn du dir bei deiner Zahl nicht sicher bist, vergiss diese Regel einfach und benutze unseren Kubikwurzel-Rechner :-)

1. Zuerst musst du die Zahl eingeben, für die du die Kubikwurzel finden möchtest.
2. Drücke √ (Wurzel-Taste) zwei Mal.
3. Drücke x (Multiplikationszeichen).
4. Drücke √ (Wurzel-Taste) vier Mal.
5. Drücke x (Multiplikationszeichen).
6. Drücke √ (Wurzel-Taste) acht Mal.
7. Drücke x (Multiplikationszeichen).
8. Drücke ein letztes Mal die Wurzeltaste zwei Mal
9. Jetzt kannst du = (Gleichheitszeichen) drücken! Hier ist deine Antwort!

Glaubst du es nicht? Überprüfe es noch einmal mit einem anderen Beispiel!

Nehmen wir an, du musst eine Kugel mit einem Volumen von 33,5 ml herstellen. Um sie herzustellen, musst du ihren Radius kennen. Wie du wahrscheinlich weißt, lautet die Gleichung zur Berechnung des Volumens einer Kugel wie folgt:

V = (4/3) ∙ π ∙ r³.

Die Gleichung für den Radius sieht also wie folgt aus:

r = ∛(3V/4π).

Du weißt, dass das Volumen 33,5 ml beträgt. Zuerst musst du in andere Volumeneinheiten umrechnen. Am einfachsten ist die Umrechnung in cm³: 33,5 ml = 33,5 cm³. Jetzt kannst du den Radius berechnen:

r = ∛(100,5/12,56)

r = ∛(8)

r = 2

Damit eine Kugel ein Volumen von 33,5 ml hat, muss ihr Radius 2 Zentimeter betragen.

Mit unserem Wurzel-Rechner kannst du auch andere Wurzeln berechnen. Schreibe einfach die Zahl in das Feld Wurzelgrad und du erhältst einen beliebigen n-ten Wurzelrechner. Unser Rechner führt automatisch alle notwendigen Berechnungen durch, und du kannst ihn frei für deine Berechnungen verwenden!

Schauen wir uns ein paar Beispiele an. Nehmen wir an, du musst die vierte Wurzel aus 1296 berechnen. Gib zuerst die entsprechende Zahl ein, aus der du die Wurzel ziehen möchtest – 1296. Dann änderst du den Grad der Wurzel in 4. Und schon hast du das Ergebnis! Die vierte Wurzel aus 1296 ist 6.

Mit unserem n-ten Wurzel-Rechner kannst du auch die Wurzel aus irrationalen Zahlen berechnen. Versuchen wir es mit der Berechnung der π-ten Wurzel. Das Symbol π steht für das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser. Sein Wert ist für jeden Kreis konstant und beträgt gerundet 3,14, aber du kannst unseren Quotientenrechner 🇺🇸 verwenden, um seinen Wert genauer zu ermitteln!

Nehmen wir an, du möchtest die π-te Wurzel aus 450 berechnen. Schreibe zunächst 450 in das Feld Radikand. Ändere dann den Grad der Wurzel – runden wir und schreiben 3,14 statt π. Und jetzt kannst du das Ergebnis sehen. Es ist fast 7.

Am Ende dieses Artikels haben wir für die hartnäckigsten unter euch einen Abschnitt über fortgeschrittene Mathematik vorbereitet. Du weißt wahrscheinlich, dass positive Zahlen immer zwei Quadratwurzeln haben: Eine negative und eine positive. Zum Beispiel: √4 = -2 und √4 = 2. Aber wusstest du, dass eine ähnliche Regel auch für Kubikwurzel gilt? Alle reellen Zahlen (außer Null) haben genau drei Kubikwurzeln: eine reelle Zahl und ein Paar komplexe Zahlen. Komplexe Zahlen wurden von Mathematikern schon vor langer Zeit eingeführt, um Probleme zu erklären, die reelle Zahlen nicht lösen können. Wir drücken sie normalerweise in der folgenden Form aus:

x = a + b ∙ i,

dabei ist x die komplexe Zahl mit dem reellen a und dem imaginären b Teil (für reelle Zahlen ist b = 0). Die geheimnisvolle imaginäre Zahl i ist definiert als die Quadratwurzel aus -1:

i = √(-1).

Gut, aber wie wirkt sich dieses Wissen auf die Anzahl der Lösungen der Kubikwurzel aus? Betrachte zum Beispiel die Kubikwurzeln von 8, die 2, -1 + i√3 und -1 - i√3 sind. Wenn du uns nicht glaubst, können wir das überprüfen, indem wir sie mit 3 exponenzieren, uns daran erinnern, dass i² = -1 ist und die kurze Multiplikationsformel (a + b)³ = a³ + 3a²b + 3ab² + b³ verwenden:

1. 2³ = 8 — die offensichtliche Lösung;
2. (-1 + i√3)³ = -1 + 3i√3 + 9 - 3i√3 = 8; und
3. (-1 - i√3)³ = -1 - 3i√3 + 9 + 3i√3 = 8.

Siehst du es jetzt? Sie sind alle gleich 8!

Die Kubikwurzel eines Produkts aus zwei Zahlen ist das Produkt der Kubikwurzeln dieser Zahlen. De Formel lautet also ∛(a ∙ b) = ∛a ∙ ∛b.

Die Antwort ist -2/3. Um dieses Ergebnis zu erhalten, gehe folgendermaßen vor:

1. Erinnere dich an die Formel ∛(a / b) = ∛a / ∛b.
2. Berechne die Kubikwurzel aus -8. Es ist klar: ∛(-8) = -2.
3. Berechne die Kubikwurzel von 27: Wir haben ∛27 = 3.
4. Das Endergebnis ist -2/3. Gut gemacht!

Der Alt-Code für das Symbol der Kubikwurzel ∛ lautet 8731. Das heißt, um ∛ zu erzeugen, musst du folgende Schritte ausführen:

1. Stelle sicher, dass du Num Lock eingeschaltet hast.
2. Drücke eine der Alt-Tasten.
3. Halte die Alt-Taste gedrückt und gib den Code 8731 im numerischen Tastenblock ein.
4. Lass die Alt-Taste los. Das Symbol der Kubikwurzel wird angezeigt.
5. Alternative Methode: Kopiere das ∛ Symbol (Strg+C) und füge es dort ein, wo du es brauchst (Strg+V).