Runden auf ganze Zahlen Rechner

Wenn die Dezimalstellen keine Rolle spielen, wird unser Rechner für das Runden auf ganze Zahlen nützlich. Mit unserem einfachen Tool erfährst du:

• Wie man auf ganze Zahlen rundet: die einfachen Regeln;

• Die Berechnungen zum Runden auf ganze Zahlen im Fall von Dezimalzahlen; und

• Einfache und ausführliche Beispiele.

Was du mit $0,\!5$ machen sollst, ist kein Geheimnis mehr: Du lernst, wie du diese immer wieder verwirrenden Zahlen in den Griff bekommst, oder entdeckst zumindest ein Tool, das das für dich erledigt!

Das Runden auf ganze Zahlen ist eine einfache mathematische Operation, die wir auf Dezimalzahlen anwenden. Ok, was ist eine Dezimalzahl? Eine Dezimalzahl ist eine Zahl, bei der wir einen ganzzahligen Teil ($1$, $2$, $3$, usw.) und einen Rest (Dezimalteil) haben. Wir trennen diese beiden Mengen mit dem Komma:

Im obigen Beispiel ist der ganzzahlige Teil rot, der Dezimalteil blau. Oft müssen wir den dezimalen Teil loswerden (z. B. weil wir ihn nicht brauchen oder, wie wir aus dem Signifikante Stellen Rechner wissen, die Genauigkeit zu hoch wäre). Das Ergebnis der Berechnungen zum Runden auf ganze Zahlen ist eine ganze Zahl, wie du schon am Namen erkennen kannst. Aber welche Regeln verwenden wir dafür?

Die folgenden Regeln gelten für jedes Intervall zwischen zwei Paaren von zusammenhängenden ganzen Zahlen (z. B. $1$-$2$, $10$-$11$, $-9$-$-8$, usw.). In jedem solchen Intervall kannst du unendliche Dezimalzahlen finden. Für die meisten von ihnen sind die Berechnungen zum Runden auf die nächste ganze Zahl ziemlich einfach. Betrachte die allgemeine ganze Zahl $i$. Hier sind die möglichen Situationen, denen du begegnen kannst, wenn du die Dezimalzahl $n$ betrachtest:

• Für $n = i,\!0$ runden wir auf $i$;

• Für $n\ \text{\textgreater}\ i,\!0$ und $n\ \text{\textless}\ i,\!5$ runden wir auf $i$ (du kannst den Dezimalteil einfach entfernen);

• Für $n=i,\!5$, schaue in den nächsten Textabschnitt;

• Für $n\ \text{\textgreater}\ i,\!5$ und $n\ \text{\textless}\ i+1,\!0$ (wobei $i+1$ die nächsthöhere ganze Zahl ist), runden wir auf $i+1$; und

• Für $n=i+1,\!0$ runden wir auf $i+1$.

Du kannst eine Symmetrie erkennen, bei der ähnliche Verhaltensweisen durch den Wert $i,\!5$ getrennt sind. Bevor wir prüfen, was im Fall von Dezimalzahlen zu tun ist, sehen wir uns einige Beispiele für die oben genannten Situationen an.

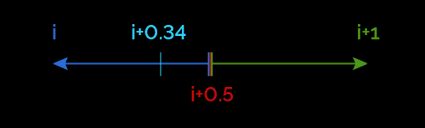
Nehmen wir die Zahl $4,\!8$. Da sie in die zweite Hälfte des Integrals fällt, runden wir sie auf $4+1 = 5$. Was ist dann mit $5,\!0$? Entferne einfach die $,\!0$: $5,\!0\rightarrow 5$.

Betrachten wir die andere Hälfte des Intervalls: Im Fall von $1,\!3$ runden wir auf $1$ ab. Was ist mit den längeren Dezimalteilen? Betrachten wir pi, $3,\!141592653589$. Ja, wie du siehst, fällt der Dezimalteil in die erste Hälfte, von $3,\!0$ und $3,\!5$: Rundet man pi auf die nächste ganze Zahl, erhält man $3$, wie dir viele Ingenieure bestätigen werden!

Für negative Zahlen gelten die gleichen Regeln!

Was passiert im Fall von Dezimalzahlen? Jede Dezimalzahl, die mit $0,\!5$ endet, hat die gleiche „Entfernung“ zu den beiden ganzen Zahlen, die das Intervall definieren. Wie runden wir dann auf die nächste ganze Zahl? Wir verwenden eine Konvention namens Aufrunden, bei der $0,\!5$ aufgerundet wird:

Beachte, dass diese Operation für negative und positive Zahlen unterschiedliche Ergebnisse liefert:

Während:

Das Aufrunden ist nicht die einzige Möglichkeit, Dezimalzahlen auf die nächste ganze Zahl zu runden.

• Das Abrunden liefert die kleinste ganze Zahl zwischen den Extremwerten: $4,\!5\rightarrow4$, und $-4,\!5\rightarrow-5$.

• Die Rundung Halbgerade liefert die abwechselnden Ergebnisse:

Beachte, dass diese Art der Berechnung der Rundung auf die nächste ganze Zahl immer eine gerade Zahl ergibt.

Beachte, dass du die Aufrundungsmethode mit der Obergrenze-Funktion ausdrücken kannst. Die „Zwillingsfunktion“, Untergrenze, gibt uns eine weitere Rundungsmethode. Schauen wir sie uns an!

Untergrenze (Floor) und Obergrenze (Ceil) sind zwei besondere mathematische Funktionen, die jeweils die nächste kleinste ganze Zahl und die nächste größte ganze Zahl liefern:

Und:

Mit diesen Funktionen definieren wir:

• Die Halbe Obergrenze, die die Obergrenze von $i,\!05$ zurückgibt: $4,\!5\rightarrow5$, und $-4,\!5\rightarrow -4$.

• Die Halbe Untergrenze, bei der du die Floor-Funktion anwendest und immer die kleinere ganze Zahl erhältst: $4,\!5\rightarrow4$, und $-4,\!5\rightarrow-5$.

Eine letzte Methode ist die sogenannte Weg von $0$. In diesem Fall runden wir Dezimalzahlen auf die ganze Zahl, die sich auf der gegenüberliegenden Seite von $0$ auf dem Zahlenstrahl befindet: $4,\!5\rightarrow5$, und $-4,\!5\rightarrow-5$.

Die Verwendung unseres Tools ist ganz einfach: Du gibst die Zahl ein und wir runden sie nach den in diesem Artikel beschriebenen Regeln auf die nächste ganze Zahl.

Unter der Optionen Erweiterter Modus findest du weitere Rundungstechniken (z. B. die gewünschte Zehnerpotenz) oder Richtlinien für Dezimalzahlen.

Das Runden auf ganze Zahlen ist nur eine von vielen Möglichkeiten, eine Zahl zu runden. Omni hat sich darum gekümmert: Probiere unsere anderen Rundungstools aus:

• Rundungsrechner (ein allgemeines Tool, das alle deine Bedürfnisse abdeckt);
• Runden auf Zehner Rechner;
• Runden auf Zehntel Rechner;
• Runden auf Hunderter Rechner;
• Runden auf Hundertstel Rechner;
• Runden auf Tausender Rechner;
• Runden auf Tausendstel Rechner 🇺🇸;
• Auf ganze Euro Runden Rechner 🇺🇸;
• Auf volle Pennys runden Rechner 🇺🇸; und
• Auf ganze Cent runden Rechner 🇺🇸.

Um eine Dezimalzahl auf die nächste ganze Zahl zu runden, sieh dir ihren Bruchteil an:

• Wenn der Dezimalteil zwischen ,0 (eingeschlossen) und 0,5 (ausgeschlossen) liegt, runde auf den ganzzahligen Teil.

• Liegt der Dezimalteil zwischen ,5 (ausgeschlossen) und ,0 (ausgeschlossen), runde die Zahl auf den ganzzahligen Teil +1.

• Wenn der Dezimalteil ,5 (Dezimalzahl) ist, rundest du immer auf die nächstgrößere ganze Zahl.

Um 4,5 zu runden, befolge diese einfachen Schritte:

1. Wähle die Rundungsmethode: Die Standardmethode ist das Aufrunden.

2. Füge 0,5 zur Zahl hinzu:

   4,5 + 0,5 = 4,0

3. Runde nach dem Standardverfahren: Das Ergebnis ist 5.

Nein! Bevor du eine Dezimalzahle rundest, solltest du dich über die geltende Regelung informieren. Hier sind die gebräuchlichsten:

• Halbe Obergrenze: Du rundest Dezimalzahlen immer auf die höchste, nächstliegende Ganzzahl;

• Halbgerade: Du rundest immer auf die nächste gerade Zahl;

• Abrunden: Du rundest immer auf die Zahl, die näher an 0 liegt;

• Halbe Untergrenze: Das Ergebnis ist immer die kleinste benachbarte ganze Zahl; und

• Abwärts von 0: runde auf die Zahl, die auf dem Zahlenstrahl von 0 entfernt liegt.

Für negative Zahlen gelten dieselben Regeln wie für positive Zahlen, wenn es darum geht, sie auf die nächste ganze Zahl zu runden, mit Ausnahme von Dezimalzahlen.

Bei Dezimalzahlen musst du eine Konvention wählen, um auf die nächstliegende Zahl zu runden. Beim Aufrunden behandelst du ,5 als „größeren“ Bruchteil und rundest die Zahl auf die ganze Zahl rechts auf dem Zahlenstrahle.