Summe und Differenz Identitäten Rechner

Willkommen bei Omni's ** Summe-und-Differenz-Identitäten-Rechner**, wo wir die Summen- und Differenzenformeln für alle sechs trigonometrischen Funktionen untersuchen, z. B. die Additionstheoreme für Sinus und Kosinus.

Summen- und Differenzidentitäten können sich als äußerst nützlich erweisen, wenn das Argument einer Funktion nicht von vornherein ein einfaches Ergebnis liefert. In solchen Fällen können wir den Winkel (und damit die Funktion) als einen Ausdruck mit angenehmeren Elementen ausdrücken. Je nach Wahl verwenden wir die Summen- oder die Differenzformel, um ein einfacheres Ergebnis zu erhalten.

Obwohl die Trigonometrie ein breites Thema mit vielen Verallgemeinerungen ist, sollten wir am Ursprung beginnen: im antiken Griechenland.

Nun gut, das war ein bisschen übertrieben, aber wir sind nicht allzu weit davon entfernt. Schließlich erinnern wir uns an die alten Griechen als diejenigen, die begannen, die Mathematik mit Formeln und Beweisen im Detail zu studieren. Vor allem die Geometrie und das Studium der Dreiecke zog ihre Aufmerksamkeit auf sich. Ein Beispiel dafür ist der berühmte Satz des Pythagoras. Und damit beginnt unsere heutige Geschichte.

Du kannst im Satz des Pythagoras Rechner mehr erfahren, aber für den Moment musst du nur wissen, dass dieser Satz die Seiten eines rechtwinkligen Dreiecks mit einer einfachen Formel in Beziehung zueinander setzt. Er sagt uns, dass die Welt der Geometrie keineswegs chaotisch ist: Es gibt Regeln, die wir befolgen müssen. Schließlich können wir leicht erkennen, dass wir, wenn wir ein beliebiges rechtwinkliges Dreieck nehmen und einen seiner spitzen Winkel vergrößern, auch einen der Schenkel entsprechend verlängern müssen. Die Trigonometrie baut auf dieser Beobachtung auf.

Die Trigonometrischen Funktionen beschreiben die Verhältnisse zwischen den Seiten eines rechtwinkligen Dreiecks. Da es sich um Verhältnisse handelt, könntest du sie theoretisch mit unserem Verhältnisrechner 🇺🇸 ermitteln – das kann sich als nützlich erweisen!

Unten findest du eine Abbildung mit Formeln, die alle sechs trigonometrischen Funktionen definieren. (Beachte, dass wir sie alle in unserem Rechner erwähnen).

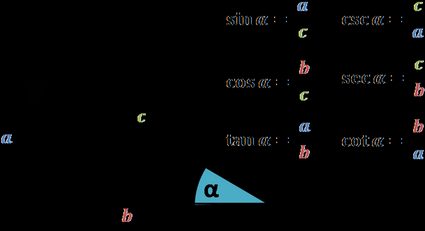
Beachte, dass die Formeln nicht erwähnen, wie groß das Dreieck ist. Darin liegt eine entscheidende Eigenschaft der Funktionen: Selbst wenn wir die Form auf die doppelte Größe skalieren, bleiben die Werte der Funktionen gleich, solange wir die Winkel beibehalten.

Allerdings haben wir zu Beginn des Abschnitts gesagt, dass die Trigonometrie ein breites Thema mit vielen Verallgemeinerungen ist, und hier sehen wir ein großes Hindernis. Wenn wir die Funktionen in einem rechtwinkligen Dreieck definieren, muss das Argument, also der Winkel, zwischen 0 und 90 Grad (oder 0 und π/2 im Bogenmaß) liegen.

Aber keine Angst! Es gibt einen Weg, das zu ändern und alle möglichen Winkel zuzulassen, auch negative. Wir müssen die ganze Argumentation nur auf einen zweidimensionalen euklidischen Raum, also eine Ebene, übertragen.

Nehmen wir an, dass A = (x,y) ein Punkt in der Ebene ist. Definiere α als den Winkel gegen den Uhrzeigersinn von der positiven Hälfte der horizontalen Achse zu dem Segment der Geraden, dessen Endpunkte (0,0) und A sind. Beachte, dass wir gesagt haben, dass α von einer Geraden zur anderen geht und nicht, dass es nur der Winkel zwischen ihnen ist. Deshalb nennen wir α oft einen gerichteten Winkel.

Natürlich kann α auch größer als 90 Grad sein. Wir können sogar Werte größer als 360 Grad (voller Winkel) zulassen – wir betrachten die 360 Grad einfach als eine komplette Runde um (0,0), und von dort aus beginnen wir einfach die zweite Runde. Und noch besser – wir können jetzt auch negative Werte verstehen! Da wir α als gerichtet definiert haben, können wir sagen, dass negative Winkel einfach die Richtung umkehren, d. h. im Uhrzeigersinn statt gegen den Uhrzeigersinn verlaufen.

Für ein solches beliebiges α und einen Punkt A = (x,y), erweitern wir die Definitionen aller sechs trigonometrischen Funktionen, indem wir die Formeln aus der obigen Abbildung wiederholen, aber mit ein paar Änderungen: Wir ersetzen b für x, a für y und c für √(x² + y²) ein, d. h. die Entfernung von (0,0) zu A.

Im Allgemeinen ist das Berechnen trigonometrischer Funktionen keine leichte Aufgabe. Normalerweise verwenden wir dafür externe Hilfsmittel, beispielsweise Omni's Trigonometrische Funktionen Rechner 🇺🇸.

Die Summen- und Differenzformeln ermöglichen es uns, den Wert einer trigonometrischen Funktion zu berechnen, indem wir sie in Form von ähnlichen Funktionen, aber mit unterschiedlichen Argumenten, beschreiben. Im Wesentlichen nehmen wir den Winkel, den wir ursprünglich erhalten haben, und zerlegen ihn in eine Summe oder Differenz von zwei anderen Winkeln. Dann können wir den Ausgangswert finden, indem wir stattdessen die neuen Winkel verwenden und dementsprechend die Summen- oder Differenzformel anwenden.

Wie wir im vorherigen Abschnitt gesehen haben, gibt es sechs trigonometrische Funktionen. Für jede gibt es eine Formel für die Winkeladdition und eine für die Winkelsubtraktion. Alles in allem sind das zwölf verschiedene (aber ähnliche) Summen- und Differenzidentitäten. Beginnen wir mit den beiden am häufigsten verwendeten Additionstheoremen für Sinus und Cosinus:

sin(α + β) = sin(α)cos(β) + cos(α)sin(β)

cos(α + β) = cos(α)cos(β) - sin(α)sin(β)

Wir sehen, dass die beiden obigen Formeln für Winkelsummen die Funktion von α + β (die von vornherein ein schwer zu handhabender Winkel sein kann) in einen Ausdruck mit separatem α und β zerlegen. Beachte auch, dass die Formeln zur Addition von Sinus und Kosinus beide Funktionen verwenden.

Insbesondere wenn die beiden Winkel gleich sind, d. h. wenn α = β ist, ergibt sich:

sin(α + α) = sin(α)cos(α) + cos(α)sin(α)

cos(α + α) = cos(α)cos(α) - sin(α)sin(α)

Wenn wir die Schreibweise vereinfachen, erhalten wir das, was oft als Doppelwinkelfunktion bezeichnet wird:

sin(2α) = 2sin(α)cos(α)

cos(2α) = cos²(α) - sin²(α)

Für den Kosinus bezieht sich der Exponent auf den Wert der Funktion, d. h. cos²(α) = (cos(α))². Mehr dazu erfährst du im Doppelwinkelfunktion Rechner 🇺🇸.

Bevor wir diesen Abschnitt abschließen, wollen wir noch einen raffinierten Trick anwenden, um die obigen Winkelsummen in Winkeldifferenzen zu verwandeln. Schließlich wissen wir ja, dass die Subtraktion einer Zahl dasselbe ist wie die Addition dieser Zahl mit umgekehrtem Vorzeichen. Mit anderen Worten: Wir können die Formeln für die Winkeladdition zu unserem Vorteil nutzen und schreiben:

sin(α - β) = sin(α + (-β)) = sin(α)cos(-β) + cos(α)sin(-β),

cos(α - β) = cos(α + (-β)) = cos(α)cos(-β) - sin(α)sin(-β).

Als Nächstes können wir die Eigenschaften von Sinus und Kosinus nutzen. Wir erinnern uns insbesondere daran, dass Sinus eine ungerade Funktion ist und Kosinus eine gerade Funktion ist. Das bedeutet, dass sin(-β) = -sin(β) und cos(-β) = cos(β) ist. Mit den obigen Formeln erhalten wir also die Differenzidentitäten von sin und cos:

sin(α - β) = sin(α)cos(β) - cos(α)sin(β)

cos(α - β) = cos(α)cos(β) + sin(α)sin(β)

Wenn wir uns die Summen- oder Differenzformeln ansehen, erkennen wir, dass das einzige, was sich ändert, das Vorzeichen in einem der Summanden ist. Der obige Trick kann auf alle Winkeladditionen angewendet werden, um die Gegenstücke zu erhalten: die Winkelsubtraktions-Identitäten.

Obwohl der Abschnitt „Additionstheoreme für Sinus und Kosinus” heißt, haben wir es auch geschafft, zwei Differenzformeln einzubauen. Das heißt, wir haben ein Drittel der trigonometrischen Summen- und Differenzidentitäten hinter uns. Wir sind mehr als bereit für den nächsten Abschnitt (#andere-trigonometrische-summen-und-sifferenzformeln) und lernen die anderen, nicht wahr?

Obwohl die Formeln für die Addition von Kosinus und Sinus am häufigsten verwendet werden, verdienen auch die anderen vier trigonometrischen Funktionen unsere Aufmerksamkeit. Im Folgenden findest du alle trigonometrischen Identitäten für Summe und Differenz. Der Vollständigkeit halber erwähnen wir auch die aus dem vorherigen Abschnitt.

• Sinus:

• Kosinus:

• Tangens:

• Kotangens:

• Sekans:

• Kosekans:

Beachte, dass es nach den ersten beiden Funktionen ein wenig komplizierter wird. Die trigonometrischen Identitäten für die Summe und Differenz von Tangens und Kotangens erfordern bereits einige Brüche. Und wenn wir uns die Summen- oder Differenzformel für Sekans und Kosekans ansehen, finden wir noch schwierigere Ausdrücke mit vielen Funktionen, die miteinander multipliziert werden.

Die Grundidee gilt aber immer noch: Auf der rechten Seite werden α und β getrennt dargestellt. Beachte auch, dass sich die Winkeladditionsformel für jede Funktion von der Differenzformel nur durch den Vorzeichenwechsel unterscheidet. Diese Eigenschaft ist eine einfache Folge des gleichen Tricks, den wir im vorherigen Abschnitt und der Parität der entsprechenden Funktionen verwendet haben.

Puh, das ist genug Theorie für heute, meinst du nicht auch? Wie wäre es, wenn wir das Ganze in die Tat umsetzen und zur Abwechslung mal ein Rechenbeispiel lösen?

Stell dir vor, du bist ein Lehrer zwischen zwei Schuljahren und möchtest herausfinden, wie du die Tische im Klassenzimmer am effektivsten anordnen kannst (wir haben auch einen Sitzabstand Klassenzimmer Rechner - Coronavirus 🇺🇸).

Du entscheidest dich für eine (grobe) Trapezform mit mehr Schülern in der ersten Reihe und weniger in den Hinteren. Allerdings hast du dein Maßband vergessen, also musst du unkonventionell vorgehen.

Mit Hilfe deines Schuhs und deiner Schrittlänge kannst du die ungefähre Entfernung zwischen den Tischen ermitteln. Du beschließt, dass der Winkel, in dem du die Tische ausrichtest, 75 Grad betragen soll (du hast das Maßband vergessen, aber nicht das Geodreieck!). Der Genauigkeit halber, stehst du irgendwann vor dem Aufgabe, den Kosinus des Winkels zu finden.

Wenn es eine Fragestellung gibt, gibt es auch eine Lösung, und der Summen- und Differenzidentität-Rechner von Omni ist das richtige Werkzeug für diese Aufgabe!

Die erste Variable des Rechners lässt uns die Funktion auswählen, mit der wir uns beschäftigen möchten. Wir brauchen den Kosinus, also wählen wir zunächst Kosinus aus der „Funktion”-Liste. Als Nächstes brauchen wir α und β – die beiden Winkel, die in der Summe und der Differenz der trigonometrischen Identitäten verwendet werden, wie die Formel über den Variablenfeldern zeigt.

Unser Winkel beträgt 75 Grad, aber wir haben keine Einschränkungen, wie wir ihn zerlegen. Wir können zum Beispiel feststellen, dass 75 = 30 + 45 ist (warum wir diese Zahlen gewählt haben, erklären wir weiter unten). Wir benutzen diese Zerlegung, um die Formel für die Winkeladdition anzuwenden, also geben wir sie in den Rechner ein:

α = 30; β = 45.

Sobald wir den zweiten Wert eingegeben haben, zeigt der Rechner dir die Antwort. Beachte, dass der Rechner die Formel Schritt für Schritt anwendet und automatisch die Differenzidentität angibt.

Für Situationen ohne Internetzugang erklären wir dir nun, wie man so eine Aufgabe schriftlich löst.

Erinnern wir uns zunächst daran, dass wir den Winkel in 75 = 30 + 45 zerlegen möchten. Um unsere Wahl zu erklären, erinnern wir daran, dass 30 und 45 Grad in zwei ganz besonderen rechtwinkligen Dreiecken vorkommen. Um genau zu sein, ist das 90-60-30 Dreieck die Hälfte eines gleichseitigen Dreiecks und das 90-45-45 die Hälfte eines Quadrats.

Das gibt uns die genauen Beziehungen zwischen den Seitenlängen der Dreiecke. Und da wir die trigonometrischen Funktionen im ersten Abschnitt als Verhältnisse zwischen den Seiten rechtwinkliger Dreiecke definiert haben, können wir all diese Informationen zusammenschreiben:

sin(30°) = 1/2, cos(30°) = √3/2

sin(45°) = √2/2, cos(45°) = √2/2

(Beachte, dass die genauen Werte mit Quadratwurzeln auch im Summen- und Differenzenrechner erscheinen.)

Schließlich rufen wir uns die Kosinus-Additionsformel in Erinnerung und wenden sie auf unseren Fall an:

cos(75°) = cos(30° + 45°)

= cos(30°)cos(45°) - sin(30°)sin(45°)

= √3/2 ∙ √2/2 - 1/2 ∙ √2/2

= √6/4 - √2/4

≈ 0,259.

Voilà! Wir haben den Kosinus berechnet; jetzt sollte es mit der Tischordnung klappen.

So berechnest du cos(15°) mit der Differenzidentität:

1. Schreibe 15° als die Differenz zwischen zwei Winkeln: 15° = 45° - 30°. Wir haben die Winkel ausgewählt, für die die Werte der trigonometrischen Funktionen leicht zu berechnen sind.

2. Wende die Formel cos(45° - 30°) = cos(45°)cos(30°) + sin(45°)sin(30°) an.

3. Setze die Werte ein: cos(45° - 30°) = √2/2 ∙ √3/2 - √2/2 ∙ 1/2.

4. Das Endergebnis ist cos(45° - 30°) = √2(√3-1)/4.

Die Formel besagt, dass der Kosinus der Differenz zweier Winkel gleich der Summe aus dem Produkt der Kosinuswerte dieser Winkel und dem Produkt ihrer Sinuswerte ist.

Die Trigonometrie hat unzählige Anwendungsmöglichkeiten. Du kannst zum Beispiel auf trigonometrische Identitäten stoßen bei:

• Kartografie;
• Ingenieurwesen;
• Astronomie;
• Navigation;
• Luftfahrt;
• Radarsysteme;
• Kriminologie;
• Medizinische Bildgebung;
• Pharmazie; und...

...viele andere!

Nicht wirklich. Du wirst natürlich die lernen, die für dein Fachgebiet am nützlichsten sind. Wenn du mit der Eulerschen Formel exp(ix) = cos(x) + isin(x) vertraut bist, kannst du die trigonometrischen Identitäten, die du für ein bestimmtes Problem brauchst, sehr effizient ableiten.