Calculadora de Identidades: Soma e Diferença

Boas-vindas à calculadora de identidades: soma e diferença da Omni, onde estudaremos as fórmulas de soma e diferença para todas as seis funções trigonométricas, por exemplo, as fórmulas da soma do seno ou do cosseno.

As identidades de soma e diferença podem se mostrar extremamente úteis sempre que o argumento de uma função não fornecer, a priori, um resultado simples. Nesses casos, podemos expressar o ângulo (e, com ele, a função) como uma equação com termos mais agradáveis. Dependendo da escolha, usamos a fórmula da soma ou da diferença para que você obtenha uma equação mais simples de lidar.

Embora a trigonometria seja um tópico amplo com muitas generalizações, devemos começar onde tudo começou: na Grécia antiga.

Ok, esta abordagem parece um pouco exagerada, mas, na verdade, não é tanto assim. Afinal de contas, foram os gregos antigos que começaram a estudar a matemática em detalhes, com fórmulas e teoremas. Em particular, a geometria atraiu a atenção deles, bem como o estudo dos triângulos. Um exemplo de onde esse fascínio os levou é o famoso teorema de Pitágoras. E é daí de onde vem a base para as fórmulas da nossa calculadora.

Você pode aprender mais sobre esse teorema na nossa calculadora do teorema de Pitágoras, mas, por enquanto, você só precisa saber que ele conecta os lados de um triângulo retângulo com uma fórmula simples. Em outras palavras, ele nos diz que o mundo da geometria não é de forma alguma caótico: existem regras que precisamos seguir. Afinal de contas, podemos ver facilmente que, se pegarmos um triângulo retângulo arbitrário e aumentarmos um de seus ângulos agudos, precisaremos alongar um dos lados de forma proporcional. A trigonometria se baseia nessa observação.

As funções trigonométricas descrevem as proporções entre os lados de um triângulo retângulo. Como se trata de proporções, você poderia teoricamente encontrá-las usando nossa calculadora de proporções, e esta pode ser mais uma ferramenta útil para você!

Abaixo você pode ver uma figura com fórmulas que definem todas as seis funções trigonométricas. Observe que todas elas aparecem em nossa calculadora de identidades trigonométricas de soma e diferença.

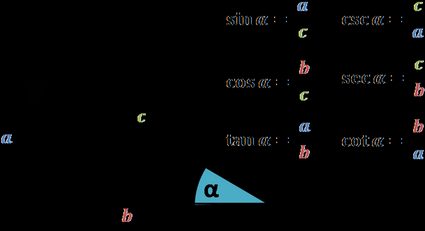
Veja como as fórmulas não mencionam o tamanho do triângulo. Na verdade, é aí que reside uma propriedade crucial das funções: mesmo se dimensionarmos a forma para o dobro de seu tamanho, os valores das funções permanecerão os mesmos, desde que mantenhamos os ângulos intactos.

No entanto, começamos a seção dizendo que a trigonometria é um tópico amplo com muitas generalizações e, aqui, vemos um obstáculo significativo. De fato, ao definir as funções em um triângulo retângulo, o argumento, ou seja, o ângulo, deve estar entre 0 e 90 graus (ou 0 e π/2 em radianos).

Mas não se preocupe! Há uma maneira de corrigir isso e permitir todos os ângulos possíveis, mesmo os negativos. Você só precisa traduzir todo o raciocínio para um espaço euclidiano bidimensional, ou seja, o plano.

Seja A = (x,y) um ponto no plano. Defina α como o ângulo no sentido anti-horário entre a metade positiva do eixo horizontal e o segmento de reta cujos pontos finais são (0,0) e A. Observe que α vai de uma reta para a outra e não é simplesmente o ângulo entre elas.

Claramente, podemos ter α maior que 90 graus. Podemos até mesmo admitir valores maiores do que o ângulo total de 360 graus, se consideramos que 360 graus são uma volta completa em torno de (0,0) e, a partir daí, apenas começamos a segunda volta. E melhor ainda: agora você também pode entender o conceito de valores negativos para os ângulos! Como definimos α como ângulos com valores positivos, podemos dizer que os ângulos negativos simplesmente são aqueles obtidos considerando o sentido oposto, ou seja, vão no sentido horário em vez de anti-horário.

Para este α arbitrário e um ponto A = (x,y), estendemos as definições de todas as seis funções trigonométricas repetindo as fórmulas da figura acima, mas com algumas alterações: substituímos b por x, a por y e c por √(x² + y²), ou seja, a distância de (0,0) até A.

Em geral, calcular funções trigonométricas não é uma tarefa fácil. Normalmente, usamos ferramentas para isso, portanto, aproveitamos esta oportunidade para direcionar você a outro recurso da Omni que certamente tornará essa tarefa muito mais fácil: a nossa calculadora de funções trigonométricas 🇺🇸.

As fórmulas de soma e diferença nos permitem calcular o valor de uma função trigonométrica descrevendo-a em termos de funções semelhantes, mas com argumentos diferentes. Em essência, pegamos o ângulo que obtivemos inicialmente e o decompomos em uma soma ou diferença de dois outros ângulos. Em seguida, podemos encontrar o valor inicial usando os novos ângulos e aplicando, de forma correspondente, a fórmula da soma ou da diferença.

Como vimos na seção anterior, há seis funções trigonométricas. Para cada uma delas, temos uma fórmula de soma de ângulos e uma fórmula de diferença de ângulos. Deste modo, ficamos com doze identidades de soma e diferença diferentes (mas semelhantes). Com esse número em mente, vamos começar com as duas mais usadas: A fórmula da soma do seno e a fórmula da soma do cosseno:

sen(α + β) = sen(α)cos(β) + cos(α)sen(β)

cos(α + β) = cos(α)cos(β) - sen(α)sen(β)

Vemos que ambas as fórmulas de soma de ângulos acima decompõem a função de α + β (que pode, ser um ângulo difícil de trabalhar) em uma expressão com funções de α e β dadas separadamente. Além disso, observe que as fórmulas de soma do cosseno e do seno usam ambas as funções.

Em particular, quando os dois ângulos são iguais, ou seja, quando α = β, as fórmulas da soma do cosseno e do seno são escritas como:

sen(α + α) = sen(α)cos(α) + cos(α)sen(α)

cos(α + α) = cos(α)cos(α) - sen(α)sen(α)

Se simplificarmos a notação, obteremos o que geralmente é chamado de fórmulas de arco duplo:

sen(2α) = 2sen(α)cos(α)

cos(2α) = cos²(α) - sen²(α)

onde, na fórmula do cosseno, o expoente se aplica ao valor da função, ou seja, cos²(α) = (cos(α))². Você pode saber mais sobre isso na nossa calculadora da fórmula do arco duplo 🇺🇸.

Antes de terminarmos esta seção, vamos aplicar um truque interessante para transformar as fórmulas da soma de ângulos acima em fórmulas de diferença de ângulos. Afinal de contas, sabemos que subtrair um número é o mesmo que somar este número com um sinal negativo. Em outras palavras, podemos usar as fórmulas de soma de ângulos a nosso favor e escrever:

sen(α - β) = sen(α + (-β)) = sen(α)cos(-β) + cos(α)sen(-β),

cos(α - β) = cos(α + (-β)) = cos(α)cos(-β) - sen(α)sen(-β).

Em seguida, podemos usar as propriedades do seno e do cosseno. Em particular, lembramos que seno é uma função ímpar e que cosseno é uma função par. Isso significa que sen(-β) = -sen(β) e cos(-β) = cos(β). Portanto, as fórmulas acima nos dão as identidades de diferença do seno e do cosseno:

sen(α - β) = sen(α)cos(β) - cos(α)sen(β)

cos(α - β) = cos(α)cos(β) + sen(α)sen(β)

Quando observamos as fórmulas de soma ou diferença, vemos que a única coisa que muda é o sinal em um dos termos. De fato, o truque que propusemos acima pode ser aplicado a todas as fórmulas de soma de ângulos para que você obtenha suas contrapartes: as identidades de diferença de ângulos.

Bem, a seção se chama “Fórmula da soma do seno, fórmula da soma do cosseno”, mas também conseguimos inserir duas fórmulas de diferença. Em média, você já tem um terço das identidades trigonométricas de soma e diferença. Estamos mais do que prontos para pular para a próxima seção e aprender sobre as outras identidades trigonométricas, não é mesmo?

Embora as fórmulas de soma do cosseno e do seno sejam as mais comuns, as outras quatro funções trigonométricas também merecem um pouco de atenção. Abaixo, você pode encontrar todas as identidades trigonométricas de soma e diferença. Para completar a nossa abordagem, mencionamos também as da seção anterior.

• Seno:

• Cosseno:

• Tangente:

• Cotangente:

• Secante:

Cossecante:

Observe que, após as duas primeiras funções, as equações começam a ficar um pouco mais complicadas. As identidades trigonométricas da soma e da diferença da tangente e da cotangente já exigem algumas frações. E se você observar a fórmula de soma ou diferença para a secante e a cossecante, verá expressões ainda piores com muitas funções multiplicadas.

No entanto, a ideia básica ainda se aplica: no lado direito das equações, α e β aparecem separadamente. Além disso, observe que, para qualquer função, a fórmula da soma de ângulos difere da fórmula da diferença apenas pela mudança de sinais. Essa propriedade é uma consequência direta do mesmo truque que usamos na seção anterior, onde consideramos a paridade das funções correspondentes.

Ufa, isso parece ser teoria suficiente para hoje, você não acha? Que tal de fazermos bom uso da nossa calculadora e resolvermos um exemplo numérico?

Digamos que você é um professor do ensino fundamental e quer reorganizar a disposição da sua sala de aula. Suponha que você queira aplicar um formato de organização das carteiras de modo a manter os novos padrões relacionados ao distanciamento social seguro. Além disso, suponha que você não conheça nossa calculadora de disposição de sala de aula 🇺🇸, então, você deve organizar as carteiras “à mão”.

Você decide manter uma forma (aproximada) de um trapézio com mais alunos na primeira fila e menos na parte de trás. No entanto, você parece ter esquecido sua fita métrica, portanto, terá de fazer as coisas de forma não convencional.

Usando seu sapato e o comprimento de cada passo, você consegue propor distâncias aproximadas entre as carteiras. Você decide que o ângulo ao longo do qual você as alinha deve ser de 75 graus (você esqueceu a fita métrica, mas não o transferidor!). Além disso, para tornar tudo mais preciso, em algum ponto do caminho, você se depara com o problema de encontrar o cosseno do ângulo.

Se você tem um problema, também tem uma solução, a calculadora de identidades: soma e diferença da Omni é a ferramenta certa para o trabalho!

A primeira variável na calculadora nos permite escolher a função com a qual estamos lidando. Precisamos do cosseno, então, vamos começar escolhendo cosseno no campo “Função”. Em seguida, precisamos inserir os valores para α e β, ou seja, para os dois ângulos usados nas identidades trigonométricas de soma e diferença, conforme a fórmula mostrada acima dos campos das variáveis.

Nosso ângulo é de 75 graus, mas não temos restrições sobre como decompô-lo. Por exemplo, podemos observar que 75 = 30 + 45 (explicaremos porque escolhemos estes números mais adiante). Usamos essa decomposição para aplicar a fórmula da soma de ângulos, de modo que a inserimos na calculadora de identidades de soma e diferença:

α = 30, β = 45

Assim que inserirmos o segundo valor, a ferramenta exibirá a resposta. Observe como a calculadora nos dá uma aplicação passo a passo da fórmula e fornece automaticamente a identidade da diferença.

Ainda assim, para as situações assustadoras em que não há internet, vejamos como encontrar a solução manualmente.

Primeiro, lembremos que gostaríamos de decompor o ângulo como 75 = 30 + 45. Para explicar nossa escolha, lembre-se de que os graus 30 e 45 aparecem em dois triângulos retângulos muito especiais. Para ser mais preciso, o triângulo 90-60-30 é, de fato, a metade de um triângulo equilátero e o 90-45-45 é a metade de um quadrado.

Isso, em particular, nos diz as relações exatas entre os comprimentos dos lados dos triângulos. Uma vez que definimos as funções trigonométricas na primeira seção deste artigo como razões entre os lados de triângulos retângulos, podemos combinar todas essas informações para escrever:

sen(30°) = 1/2, cos(30°) = √3/2

sen(45°) = √2/2, cos(45°) = √2/2

Observe como os valores exatos com raízes quadradas também aparecem na calculadora de identidades: soma e diferença.

Por fim, relembramos a fórmula da soma do cosseno e a aplicamos ao nosso caso:

cos(75°) = cos(30° + 45°)

= cos(30°)cos(45°) - sen(30°)sen(45°)

= √3/2 ⋅ √2/2 - 1/2 ⋅ √2/2

= √6/4 - √2/4

≈ 0,259

Temos nosso cosseno; agora, a organização da sala deve ser tranquila. Esperamos que as crianças respeitem o novo posicionamento das carteiras para que o esforço não seja em vão.

Para calcular cos(15°) com a identidade trigonométrica da diferença:

1. Escreva 15° como a diferença entre dois ângulos: 15° = 45° - 30°. Escolhemos os ângulos para os quais os valores das funções trigonométricas são fáceis de calcular.

2. Aplique a fórmula cos(45° - 30°) = cos(45°)cos(30°) + sen(45°)sen(30°).

3. Insira os valores: cos(45° - 30°) = √2/2 ⋅ √3/2 - √2/2 ⋅ 1/2.

4. O resultado final é cos(45° - 30°) = √2(√3-1)/4.

A identidade diz que o cosseno da diferença de dois ângulos é igual à soma do produto dos cossenos desses ângulos e do produto de seus senos.

A trigonometria tem inúmeras aplicações. Por exemplo, você pode se deparar com identidades trigonométricas em:

• Cartografia;
• Engenharia;
• Astronomia;
• Navegação;
• Aviação;
• Sistemas de radar;
• Criminologia;
• Imagens médicas;
• Farmácia; e...

… muitos outros casos!

Na verdade, não. Você aprenderá naturalmente aquelas que são mais úteis em seu campo de especialização. Na verdade, se você estiver familiarizado com a fórmula de Euler exp(ix) = cos(x) + isen(x), poderá derivar com muita eficiência as identidades trigonométricas necessárias em um determinado problema.