Zugkraft Rechner

Mit diesem Zugkraft Rechner lernst du, wie du die Kraft in einem Seil oder einer Schnur zum Anheben eines Objekts berechnen kannst. Du erfährst, wie man die Zugkraft in Seilen ermittelt, die zum Zug eines Objekts auf einer reibungsfreien Oberfläche verwendet werden. Außerdem zeigen wir dir zur Verdeutlichung der Berechnung der Zugkräfte eine Reihe von Freikörper-Diagrammen. Wenn du mehr über die Zugkraft und ihre Formel erfahren möchtest, lies weiter!

Stell dir vor, du hebst einen Basketball vom Boden auf. Du spürst das Gewicht des Balls in deinen Händen, da die Schwerkraft auf die Masse des Balls wirkt. Jetzt stell dir vor, du bindest ein Seil um den Ball und hebst ihn damit wieder hoch. Du würdest das Gewicht des Balls immer noch durch das Seil spüren. Das Seil steht unter Zug. Die Zugkraft hält das Seil zusammen. Wenn du das Seil durchschneidest, wird diese Kraft aufgehoben und die Kugel fällt.

Die Zugkraft ist eine axiale Kraft, die durch ein unter Zug stehendes Objekt, wie ein Seil, eine Schnur oder eine Kette, wirkt. Wir können die Zugkraft auch bei anderen Materialien wie Stäben und Stangen beobachten, wenn sie einer äußeren Zugkraft ausgesetzt sind. Materialien mit hoher Zugfestigkeit eignen sich am besten für Stäbe und Stangen, da sie unter Zug nicht so leicht brechen. In unserem Spannungsrechner, in dem es um Elastizität geht, erfährst du mehr über Zugfestigkeit.

Die Zugkraft ist auch ein gutes Beispiel für das dritte Newtonsche Gesetz. Newtons drittes Gesetz besagt, dass, wenn ein Körper eine Kraft auf einen zweiten Körper ausübt, übt der zweite Körper eine gleich große Kraft in die entgegengesetzte Richtung auf den ersten Körper aus. Die Zugkraft ist eine reaktive Kraft, die einer äußeren Zugkraft entgegenwirkt.

Um die in einem Seil wirkende Zugkraft zu berechnen, müssen wir zunächst das zweite Newtonsche Gesetz verstehen. Dies besagt, dass die Summe der Kräfte, die auf ein Objekt mit konstanter Masse wirken, gleich der Masse dieses Objekts multipliziert mit seiner Beschleunigung ist. Wir können diese Aussage auch in einer Gleichung ausdrücken:

ΣF = m × a

wobei:

• Σ (sigma) bezeichnet die Summe der Kräfte F;
• m ist die Masse des Objekts; und
• a die Beschleunigung.

Für ein Objekt, das an einem Seil aufgehängt ist, können wir die Gravitationsbeschleunigung 🇺🇸 g verwenden. Die Gravitationsbeschleunigung gibt uns den Wert des Gewichts als Kraft an, z. B. in Newton oder Kraftpfund. Wenn sich das Objekt mit einer anderen Beschleunigung bewegt, sollten wir seine tatsächliche Beschleunigung für die Berechnung verwenden. Dieser Spannungsrechner ermittelt jedoch nur die Spannungskräfte im Falle eines statischen Gleichgewichts.

Diese Aussage bedeutet, dass dieses Tool nur ruhende Objekte in einem bestimmten System berücksichtigt. In diesem Zugkraft Rechner gehen wir außerdem davon aus, dass Seile masselos sind und daher nichts zu den Zugkräften beitragen. Wir gehen ebenfalls davon aus, dass sich Massen oder Objekte in einem Vakuum befinden und keine Reibung oder Luftwiderstand auf sie wirkt.

In der folgenden Abbildung sehen wir, dass die Kraft F, die zum Anheben des Objekts benötigt wird, gleich dem Gewicht W des Objekts ist. Dieser Gedanke ist das grundlegende Konzept unserer Formel für Zugkräfte. Des Weiteren ist ein Freikörperdiagramm des Objekts zu sehen, das auf die Schnur wirkende Zugkräfte T zeigt. Wie du sehen kannst, treten die Zugkräfte paarweise und in entgegengesetzter Richtung auf:

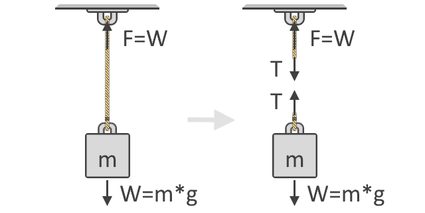
Nach dem zweiten Newton’schen Gesetz können wir die Summe der Kräfte mithilfe des Freikörperdiagramms des Objekts ausdrücken, wie auf der rechten Seite der obigen Abbildung zu sehen ist. Wir verwenden Freikörperdiagramme, um die verschiedenen Richtungen und Größenordnungen der Kräfte darzustellen, die auf einen Körper wirken. Im Gleichgewicht sollten diese Kräfte summiert Null ergeben. Wenn wir alle nach oben gerichteten Kräfte als positiv und alle nach unten gerichteten Kräfte als negativ betrachten, lautet unsere Gleichung:

ΣF↑ = 0 = T + (-W)

T = W

wobei das Gewicht W negativ wird, da es nach unten gerichtet ist. Wenn wir die Gleichung nach W auflösen, sehen wir, dass die Zugkraft im Seil gleich dem Gewicht des getragenen Objekts ist.

Wenn wir mehrere Seile zum Heben eines Gegenstands verwenden, wird die gesamte Zugkraft auf die einzelnen Seile aufgeteilt. Die Zugkraft in jedem Seil hängt von seinem Winkel zur entgegenwirkenden Kraft ab. Zur Verdeutlichung betrachten wir ein weiteres Freikörperdiagramm eines Objekts, das an zwei Seilen aufgehängt ist:

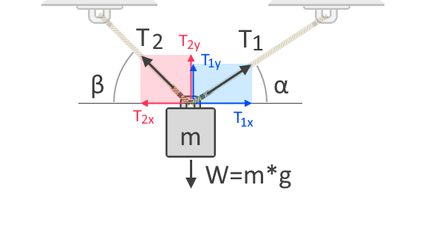
Im obigen Freikörperdiagramm sehen wir die horizontalen und vertikalen Komponenten der Zugkräfte T₁ und T₂. Kräfte sind Vektoren, das heißt, sie besitzen sowohl eine Größe als auch eine Richtung. Wie alle Vektoren können Kräfte in diesen Komponenten ausgedrückt werden, die den Einfluss der Kraft entlang der horizontalen und vertikalen Achse angeben. T₁ₓ und T₂ₓ beschreiben die horizontale Komponenten von T₁ bzw. T₂. T_1y und T_2y drücken die vertikalen Komponenten derselben Kräfte aus. Da die Schwerkraft in der Vertikalen auf das Objekt einwirkt, müssen wir die vertikale Komponente der Zugkräfte bei der Summierung der Kräfte wie folgt berücksichtigen:

ΣF↑ = 0 = T_1y + T_2y + (-W)

W = T_1y + T_2y

Da die Winkel der Zugkräfte gegeben sind, können wir T_1y und T_2y mithilfe trigonometrischer Funktionen in T₁ bzw. T₂ ausdrücken:

T_1y = T₁ × sin(α)

T_2y = T₂ × sin(β)

W = T₁ × sin(α) + T₂ × sin(β)

Damit das System im Gleichgewicht ist, sollte sich das Objekt nicht horizontal oder entlang der x-Achse bewegen. Daher müssen die horizontalen Komponenten von T₁ und T₂ Null ergeben. Mithilfe der Trigonometrie können wir T₁ₓ und T₂ₓ in Form von T₁ bzw. T₂ ausdrücken:

T₁ₓ = T₂ₓ

T₁ × cos(α) = T₂ × cos(β)

Wenn wir beide Seiten durch cos(α) dividieren, erhalten wir eine Gleichung, in der T₁ in Form von T₂ und den Winkeln ausgedrückt wird:

T₁ = T₂ × cos(β) / cos(α)

Mit dieser Gleichung können wir nach T₂ auflösen, indem wir T₂ × cos(β) / cos(α) als T₁ in unsere Gleichung zur Summierung der Kräfte einsetzen:

W = T₁ × sin(α) + T₂ × sin(β)

W = T₂ × [cos(β) / cos(α)] × sin(α) + T₂ × sin(β)

W = T₂ × [cos(β) × sin(α) / cos(α) + sin(β)]

T₂ = W / [cos(β) × sin(α) / cos(α) + sin(β)]

Multiplizieren wir schließlich diese ganze Gleichung mit cos(β) / cos(α), wie wir es in dem Wert von T₁ in Bezug auf T₂ abgeleitet haben, erhalten wir:

T₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]

T₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]

T₁ = W / [cos(α) × sin(β) / cos(β) + sin(α)]

Jetzt musst du nur noch die Winkel der Zugseile gegenüber der Horizontalen kennen. Wenn nur ein Winkel von der Vertikalen gegeben ist, ziehst du diesen einfach von 90° ab. Auf diese Weise erhältst du den Winkel zur Horizontalen. Wenn du jedoch andere Winkelwerte erhältst, die größer als 90° oder sogar 180° sind, möchtest du vielleicht unseren Referenzwinkel Rechner 🇺🇸 benutzen, um den benötigten Winkel zu bestimmen. Nachdem wir die Werte für die Variablen in unseren Formeln für die Zugkräfte bestimmt haben, können wir nun die Zugkräfte berechnen.

Die Berechnung der Kraft, die auf ein gezogenes Objekt einwirkt, ist ähnlich wie beim Aufhängen. Der einzige Unterschied ist, dass wir zuerst die Beschleunigung des gesamten Systems berechnen und alle Kräfte entlang der Horizontalen summieren müssen. Wenn das Seil schräg zum Boden liegt, müssen wir auch die horizontale Komponente der Zugkraft berechnen.

Schauen wir uns das folgende Beispiel an, um besser zu verstehen, wie man die Zugkraft eines Seils ermittelt, das einen oder zwei Gegenstände zieht. In diesem Beispiel werden zwei Gegenstände von einer einzigen Zugkraft gezogen. Ein weiteres Seil zieht das zweite Objekt, das am ersten Objekt befestigt ist, wie unten dargestellt:

Diese Abbildung zeigt, dass die Massen von m₁ und m₂ 3 kg bzw. 2 kg betragen. Die Summe dieser beiden Massen ergibt die Gesamtmasse des Systems, 5 kg. Wir müssen auch die horizontale Komponente der Zugkraft T = 24 N bestimmen, die in einem Winkel θ = 60° wirkt. Mithilfe trigonometrischer Funktionen können wir die horizontale Komponente der Zugkraft berechnen: 24 N × cos(60°) ergibt 12 N . Da wir nun die horizontale Komponente der Zugkraft und die Gesamtmasse des Systems kennen, können wir die Beschleunigung a des Systems wie folgt berechnen:

F = m × a → a = F / m

a = 12 N / 5 kg = 2,4 m/s²

Nachdem wir die Beschleunigung des Systems ermittelt haben, können wir das Zweite Newton’sche Gesetz erneut anwenden, um die Seil- oder Schnurspannung des Systems zu berechnen. Dazu multiplizierst du die Beschleunigung mit der Masse, an der das Seil zieht. Im Freikörperdiagramm für T₂ erkennen wir, dass es nur auf die Masse m₂ wirkt: T₂ = a × m₂. Somit berechnen wir für T₂ = (2,4 m/s²) × (2 kg) = 4,8 N. Andererseits ist T₁ die Zugkraft, die sowohl das Gewicht m₁ als auch m₂ zieht. Der Wert für T₁ ist bereits gegeben: T₁ = 24,0 N.

Würden wir in unserem Beispiel nur ein einziges Seil verwenden, könnten wir diesen Aufbau mit einem Riemengetriebe vergleichen. Ein Riemengetriebe ist eine einfache Maschine, die die Kräfte der Seile ausnutzt, um einen mechanischen Vorteil zu erzielen. In unserem Riemenscheiben Rechner und Riemenlänge Rechner (für ein System mit zwei Rollen) erfährst du mehr über den mechanischen Vorteil und die Spannung.