Maßstab Rechner

Dieser Rechner hilft dir dabei, den Abstand zwischen zwei Objekten oder die Größe von skalierten/echten Strukturen für einen bestimmten Maßstab zu finden. Lies weiter, um eine Antwort auf die Frage „Was ist ein Maßstabsfaktor?” zu finden! Lerne, wie du einen Maßstabsfaktor berechnest, entdecke, dass die Maßstabsumrechnung viel mit der Längenumrechnung gemeinsam hat, und beende den Umrechnungs-Kampf mit Maßstäben!

Der Maßstabsfaktor kann als ein Verhältnis zwischen zwei Zahlen definiert werden (mehr darüber erfährst du im Quotientenrechner 🇺🇸). Er kann sowohl größer als auch kleiner als Eins sein, je nachdem, ob das skalierte Objekt vergrößert oder verkleinert wird.

Das Konzept des Maßstabs wird in vielen Bereichen verwendet, zum Beispiel in der Mathematik, der Geografie oder der Wirtschaft. Wir finden Maßstäbe oft, wenn wir die Anleitung eines maßstabsgetreuen Modells oder die Legende eines Stadtplans lesen.

Es gibt verschiedene Möglichkeiten, um den Maßstab darzustellen:

• Numerischer Maßstab — dieser ist dimensionslos. Die Form 1:1000 bedeutet, dass der Maßstabsfaktor 0,001 beträgt. Jedes Verhältnis von zwei Zahlen ist korrekt, aber es ist üblich, dass eine der beiden Zahlen 1 beträgt, z. B. 2,5:1 statt 5:2. Wenn eine der Zahlen keine ganze Zahl ist und gleichzeitig kleiner als 10 000 ist, lohnt es sich, die Anzahl der Nachkommastellen zu berücksichtigen.

  In diesem Maßstab-Rechner empfehlen wir, bis zu 5 signifikante Stellen für Dezimalzahlen zu verwenden oder das Ergebnis auf die nächste ganze Zahl zu runden. Wir können eine numerische Skala zur Berechnung der vertikalen Überhöhung verwenden, um bestimmte Objekte auf 3D-Karten und Zeichnungen hervorzuheben. Weitere Informationen dazu findest du in unserem Vertikale Überhöhung Rechner 🇺🇸!

• Maßstab als Text — wird in Worten ausgedrückt, z. B. „ein Zentimeter zu einem Kilometer” oder äquivalent 1 cm : 1 km. Wir verwenden diese Form meist für Karten, und die Umrechnung sagt aus, dass 1 cm auf der Grafik einer tatsächlichen Entfernung von 1 km entspricht. Wir können auch eine Beschreibung finden, die die Größe des skalierten Objekts als Prozentsatz des realen Objekts angibt.

• Linearer (grafischer) Maßstab — zeigt die Abmessungen des Objekts oder der Karte auf grafische Weise. Diese Darstellung ist sehr natürlich und intuitiv. Wenn du den Maßstab von Punkt A nach Punkt B legst, siehst du sofort die Entfernung zwischen den beiden Punkten. Du musst keine Berechnungen anstellen! Selbst wenn du eine Karte mit einem solchen Maßstab in einem größeren Format nachdrucken möchtest, ist das kein Problem, denn der Maßstab wird automatisch vergrößert.

  Wenn wir im folgenden Beispiel davon ausgehen, dass der Abstand zwischen den großen Strichen 1 cm beträgt, entspricht das einer realen Länge von 1 km, und der Maßstab entspricht dann 1 cm : 1 km oder 1:100 000.

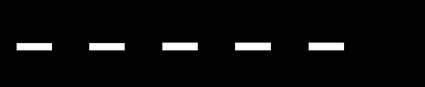
Grafische Skalen müssen nicht unbedingt eine Verbindung zwischen denselben physikalischen Größen darstellen. Zum Beispiel kann der Abstand zwischen zwei Punkten ein Zeit-Intervall von einer Sekunde bezeichnen. Diese Art der Umrechnung findest du in den meisten Diagrammen.

Bei der Datenanalyse ist es manchmal sinnvoller, die logarithmische Skala zu verwenden. Dabei ist das Verhältnis und nicht die Differenz zwischen benachbarten Punkten konstant. Auf diese Weise ist es möglich, Werte im Bereich mehrerer Größenordnungen im selben Diagramm nebeneinander darzustellen.

Wir halten uns bei Konstruktions- oder Landschaftsbauprojekten meistens an die am häufigsten verwendeten Architekturmaßstäbe. Es ist nicht nötig, sie auswendig zu lernen, aber es ist wirklich praktisch, die Erklärungen dafür an einem Ort zu haben und zu wissen, wie man den Maßstabsfaktor schnell berechnet. In der folgenden Tabelle sind einige Beispiele aufgelistet, die dir nützlich sein können:

Es mag dich überraschen, aber die Maßstabsumrechnung für Flächen und Volumen ist nicht so offensichtlich wie für Entfernungen. Der Maßstab sagt normalerweise etwas über das Verhältnis zwischen der skalierten und der ursprünglichen Länge aus, was bedeutet, dass sich beide Dimensionen ändern müssen.

Wenn der Maßstabsfaktor gleich f ist, dann ist das Verhältnis zwischen dem skalierten und dem realen Flächeninhalt gleich f², und für das Volumen gleich f³.

Nehmen wir an, du möchtest den Umfang eines Kreises um den Faktor 2 verkleinern. Dann kannst du sofort feststellen, dass der neue Flächeninhalt 4 Mal kleiner ist. Andererseits fragst du dich vielleicht, wie du den Skalierungsfaktor zwischen zwei Flächen oder Volumina ermitteln kannst – berechne einfach das Verhältnis von skaliertem und realem Wert. Der Skalierungsfaktor, der dein Modell beschreibt, ist bei Flächeninhalten die Quadratwurzel und bei Volumina die Kubikwurzel.

In diesem Maßstab-Rechner musst du dir darüber keine Gedanken machen. Du kannst einfach die Option auswählen, für die du den Maßstab finden möchtest.

Nehmen wir an, du hast einen Plan für deinen Traum-Gartenschuppen gefunden. Auf einer maßstabsgetreuen Modellbauanleitung steht geschrieben, dass die Länge 10 cm, die Breite 8 cm und die Höhe 5 cm beträgt. Du möchtest deinen Schuppen aber mit einer Länge von 5 m bauen, bei dem die Proportionen der anderen Maße erhalten bleiben.

1. Bestimme den Maßstabsfaktor: 10 cm / 5 m = 0,02.

2. Schreibe ihn in Form eines numerischen Maßstabs auf, 1:50, damit du dir den Maßstab deines Projekts merken kannst.

3. Berechne die restlichen Maße – Breite: 8 cm / 0,02 = 4 m, Höhe: 5 cm / 0,02 = 2,5 m.

4. Du kannst das Gesamtvolumen des Gartenschuppens berechnen, damit du dir sicher sein kannst, dass alle deine Gartengeräte hineinpassen: 5 m ∙ 4 m ∙ 2,5 m = 50 m³.

Wie du siehst, ist es ein Kinderspiel, die endgültige Größe der Gartenschuppen-Wände mithilfe unseres Maßstab-Rechners zu berechnen. Allerdings wird das Gesamtbild nicht sehr beeindruckend sein, wenn die Konstruktion nur kahle Wände ohne Dach hat. Das kannst du aber ändern – sieh dir unseren Dachfläche Rechner an und schaffe einen wunderschönen Platz in deinem Garten!

Um die Entfernung zwischen zwei Objekten anhand ihrer Kartendistanz zu bestimmen:

1. Bestimme die Entfernung zwischen diesen Objekten auf der Karte.

2. Wende die Maßstabsumrechnung an: Kartenabstand / Maßstabsfaktor.

3. Das Ergebnis, das du erhältst, ist der reale Abstand zwischen den beiden Objekten.

Ein Maßstab von 1:100 bedeutet, dass die Entfernung auf der Karte 100 Mal kleiner ist, als die Entfernung in der realen Welt. Das heißt, dass 1 Zentimeter (0,01 Meter) auf der Karte gleich 100 cm (1 Meter) in der realen Welt entspricht.

100 Meter. Der Maßstab 1:1000 bedeutet, dass 1 cm auf der Karte 1000 cm entspricht, was 10 m entspricht. 10 cm auf der Karte entsprechen also 100 m in der realen Welt.