Calculadora de desfase

Bienvenido a la calculadora de desfase de Omni, donde estudiaremos las funciones trigonométricas y cómo calcular su desplazamiento de fase. El desplazamiento de fase también se conoce como traslación horizontal, desplazamiento horizontal, desfase, diferencia de fase o cambio de fase. Aquí os enseñaremos a calcularlo independientemente del nombre que uses y además también explicaremos cómo hallar la amplitud y cómo hallar el periodo. De hecho, resulta que una enorme clase de funciones se comportan prácticamente igual, y las diferencias se reducen a describir los mismos valores antes mencionados: la amplitud, el periodo y el desplazamiento de fase. Bueno, salvo un desplazamiento vertical.

Como hemos dicho antes, nos centraremos aquí en las funciones trigonométricas: más concretamente en el seno y el coseno. Sin embargo, es importante recordar que muchas de las nociones son más generales, especialmente las de traslación horizontal o desplazamiento vertical.

En primer lugar, veamos una imagen que muestra en la gráfica la amplitud, el periodo, el desplazamiento de fase y el desplazamiento vertical (observa que la misma imagen aparece en la parte superior de la calculadora).

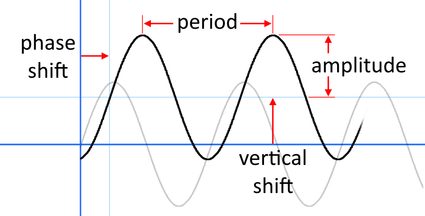
Podemos escribir esas funciones con la fórmula de desfase:

o:

donde $A$, $B$, $C$, $D$ son números reales arbitrarios, pero con $A$ y $B$ distintos de cero (de lo contrario, no sería una función trigonométrica). Obviamente, esos cuatro números determinan la amplitud, el periodo, el desplazamiento de fase y el desplazamiento vertical. La imagen muestra cómo afectan a la función. Aun así, sería útil apoyar las imágenes con algunas definiciones.

1. La amplitud es la distancia (en vertical) que recorren los valores desde la línea central del gráfico, y = 0. Para un seno o coseno simple, su valor es $1$, ya que la línea central está en $0$, y los valores de la función van de $-1$ a $1$.

2. El periodo es la longitud en el eje horizontal, tras la cual la función se repite. En otras palabras, la gráfica (infinita) no es más que un montón de copias concatenadas, una detrás de otra; la longitud de este segmento copiado es el periodo. Para un seno o coseno simple, el periodo es igual a $2\pi$, ya que $\text{sen}(0) = \text{sen}(2\pi) = \text{sen}(4\pi) = …$ y las partes intermedias son exactamente iguales (y lo mismo para el coseno).

3. El desplazamiento de fase (también llamado desplazamiento horizontal o traslación horizontal) describe cuánto se ha desplazado horizontalmente la gráfica respecto al seno o coseno regular. Como tal, el valor es igual a $0$ si tenemos las dos funciones inalteradas.

4. El desplazamiento vertical (también llamado traslación vertical) describe cuánto se ha desplazado verticalmente la gráfica respecto al seno o coseno regular. En otras palabras, es el gemelo del desplazamiento de fase que se refiere a la dirección perpendicular. En concreto, el valor vuelve a ser igual a $0$ si tenemos la función sin alterar.

Bien, ya hemos aprendido qué es el desplazamiento de fase, así como los tres valores que lo acompañan. Las secciones siguientes describen cómo calcular cada uno de ellos a partir de la notación de la fórmula de desfase anterior. En primer lugar, mostramos cómo hallar la amplitud.

El concepto que hemos introducido está muy extendido en el estudio de los movimientos oscilatorios y armónicos. Por decirlo todo, esos fenómenos son los mejores amigos de la trigonometría. Puedes descubrir la conexión en nuestra calculadora de trigonometría o aprender más sobre las diversas funciones que aparecen continuamente cuando analizas un péndulo en la calculadora de funciones trigonométricas 🇺🇸, ¡o en las más específicas calculadora de coseno 🇺🇸 y calculadora de seno 🇺🇸!

Sabemos que las funciones seno y coseno tienen valores comprendidos entre $-1$ y $1$. Es más, ese simple hecho no cambia si sustituimos $\text{sen}(x)$ o $\cos(x)$ por $\text{sen}(Bx - C)$ o $\cos(Bx - C)$ (para un $B$ distinto de cero y $C$ arbitrario). De hecho, se debe a que la función $f(x) = Bx - C$ es entonces una biyección (es decir, una correspondencia de uno a uno) sobre el espacio de los números reales.

Veamos ahora qué ocurre si añadimos $D$, es decir, si en su lugar tenemos $\text{sen}(Bx - C) + D$ o $\cos(Bx - C) + D$. Dado que la primera parte da algo entre $-1$ y $1$, el conjunto estará entre $-1 + D$ y $1 + D$ (véase Cómo hallar el desplazamiento vertical para comparar). Eso significa que la línea central cae en $D$, y la amplitud sigue siendo $1$ porque los valores no se alejan más de $1$ con respecto a $D$.

Por tanto, lo único que puede afectar a la amplitud en la fórmula de desfase $A\cdot \text{sen}(Bx - C) + D$ y $A\cdot\cos(Bx - C) + D$ es el valor distinto de cero $A$. Y efectivamente, como $\text{sen}(Bx - C)$ y $\cos(Bx - C)$ están todo este tiempo entre $-1$ y $1$, el multiplicador $A$ cambia este rango a $-1\cdot A = -A$ y $1 \cdot A = A$.

Sí, lo has adivinado: la amplitud de la fórmula de desfase $A \cdot \text{sen}(Bx - C) + D$ y $A \cdot\cos(Bx - C) + D$ es simplemente igual a $A$.

Recordemos que las funciones seno y coseno tienen periodos iguales a $2\pi$, es decir, tenemos $\text{sen}(x + 2\pi) = \text{sen}(x)$ y $cos(x + 2\pi) = cos(x)$ para cualquier $x$. En particular, eso da

y:

Por tanto, vemos que $A$ y $D$ en la fórmula de desfase no tienen ningún efecto sobre el periodo. De hecho, todo se reduce a lo que ocurre dentro de las funciones trigonométricas. Y, sin embargo,

y:

Por las mismas reglas que antes, así que no es la $C$, ni la una, ni la otra, la que hace el trabajo. Así que, descartadas tres opciones, debe ser la cuarta: el $B$.

Volvemos a recurrir al comentario con el que empezamos para entender por qué y cómo $B$ afecta a la periodicidad en la fórmula de desfase $A \cdot \text{sen}(Bx - C) + D$ y $A \cdot \cos(Bx - C) + D$. Al fin y al cabo:

Así, con cada $2\pi/B$ añadido al argumento $x$, volvemos al mismo punto, y la función se repite (y lo mismo para el coseno).

En definitiva, el periodo de una ecuación de desfase es igual a $2\pi/B$.

Nuestra experiencia de las ondas suele dar prioridad a la frecuencia sobre el periodo; sin embargo, son casi la misma cosa. Descubre por qué en la calculadora de frecuencia de Omni.

Por definición, el desfase describe la traslación horizontal de la función respecto a la función regular $\text{sen}(x)$ o $\cos(x)$. Como tal, las funciones básicas lo tienen igual a $0$. De hecho, si comparamos sus gráficas de seno y coseno:

...nos daremos cuenta de que podemos obtener una traduciendo la otra (de hecho, las cofunciones mutuas tienen muchas similitudes). Para ser precisos, tenemos lo siguiente

y:

El ejemplo anterior ya sugiere dónde, en $A \cdot\text{sen}(Bx - C) + D$ y $A \cdot\cos(Bx - C) + D$, debemos buscar los valores responsables de los desplazamientos de fase. Sin embargo, a diferencia de la amplitud y el periodo, esta vez, necesitaremos dos de las cuatro letras.

En general, (es decir, no solo en la fórmula de desfase), obtenemos la traslación horizontal de una función arbitraria $f(x)$ calculando $f(x - a)$: el desplazamiento de la gráfica $a$ hacia la derecha. En otras palabras, sustituimos cada aparición de $x$ por $x - a$ en la fórmula de $f(x)$. Por ejemplo, aplicando la traslación a $\text{sen}(x)$ se obtiene $\text{sen}(x - a)$, pero para, digamos, $\cos(3x + 1)$ obtendríamos:

En otras palabras, no podemos olvidarnos de los multiplicadores que están delante de $x$.

En nuestro caso, la fórmula de desfase da:

que es un desplazamiento de fase de $C/B$ (hacia la derecha) de la función $A \cdot \text{sen}(Bx)$. Por supuesto, también podemos repetir lo anterior para el coseno.

En resumen, para calcular el desfase de la fórmula de desfase, hay que encontrar $C/B$.

Esta es fácil, sobre todo ahora que hemos visto qué son el desfase, la amplitud y el periodo y cómo calcularlos. Basémonos en lo que hemos aprendido hasta ahora.

Sabemos que en la fórmula de desfase $A \cdot \text{sen}(Bx - C) + D$ y $A \cdot\cos(Bx - C) + D$, la $A$ determina cuánto fluctúan los valores a ambos lados de la línea $y = 0$. El $B$ especifica hasta dónde extendemos el alcance del gráfico y, en consecuencia, a qué velocidad llegamos a repetir los valores. Además, junto con $C$, ambos describen si hemos desplazado la función hacia la izquierda o hacia la derecha y cuánto.

Obviamente, la traslación horizontal no afecta al desplazamiento vertical: al fin y al cabo, son dos direcciones perpendiculares. Por otra parte, la amplitud solo nos dice hasta dónde llega verticalmente la gráfica, pero no la desplaza. En definitiva, nos quedamos con una sola letra: $D$.

La $D$ en la fórmula de desfase es precisamente el desplazamiento vertical. Determina el alcance de la función, es decir, a qué distancia de la versión habitual, no $D$, desplazamos la gráfica.

Con esto concluye la parte teórica por hoy. Es hora de ver cómo calcular el desplazamiento de fase en un bonito ejemplo. ¿Y sabes qué? Mostraremos también cómo hallar el periodo, la amplitud y el desplazamiento vertical. Al fin y al cabo, ¿por qué no? Más cálculo matemático = ¡más diversión!

Veamos cómo hallar la amplitud, el periodo, el desplazamiento de fase y el desplazamiento vertical de la función $f(x) = 0.5 \cdot \text{sen}(2x - 3) + 4$. En primer lugar, dejaremos que hable la calculadora de desfase de Omni.

En la parte superior de nuestra herramienta, tenemos que elegir la función que aparece en nuestra fórmula. Para nuestro caso, elegimos “seno” en “La función trigonométrica en f”. Eso activará una representación simbólica de la ecuación de desfase: $f(x) = A \cdot \text{sen}(Bx - C) + D$. Mirando lo que tenemos, introducimos lo siguiente:

Observa cómo incluso antes de que introduzcamos los valores, la calculadora desfase muestra la gráfica de la función $\text{sen}(x)$. Esto se debe a que la herramienta entiende los campos vacíos como los valores de las fórmula regular. Por lo tanto, si no hay valores, la calculadora los interpreta como $A = 1$, $B = 1$, $C = 0$, y $D = 0$, lo que da:

En el momento en que damos el último valor, aparece debajo la gráfica de la función junto con la amplitud, el periodo, el desplazamiento de fase y el desplazamiento vertical más abajo. Observa también que, si es necesario, puedes entrar en el modo avanzado de la calculadora para hallar el valor de la función en cualquier punto $x_0$.

Ahora vamos a explicar cómo encontrar nosotros mismos el desplazamiento de fase y todos los demás valores. Para ello, basta con recordar los cuatro apartados anteriores para calcularla:

• La amplitud es $A = 0.5$;
• El periodo es $2\pi / B = 2\pi / 2 = \pi$;
• El desfase es $C / B = 3 / 2 = 1.5$; y
• El desplazamiento vertical es $D = 4$.

En total, el gráfico tiene este aspecto:

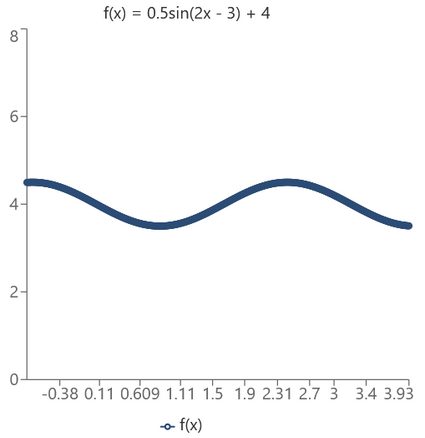
Pan comido, ¿verdad? Asegúrate de jugar con la calculadora de desfase para ver cómo afectan los distintos coeficientes al gráfico.

Para calcular el desfase de una función de la forma A × sen(Bx - C) + D o A × cos(Bx - C) + D, necesitas:

1. Determinar B.
2. Determinar C.
3. Dividir “C/B”.
4. Recordar que si el resultado es:
   • Positivo, la gráfica se desplaza a la derecha.
   • Negativo, la gráfica se desplaza a la izquierda.
5. Disfrutar de haber encontrado el desfase.

Para encontrar el desfase a partir de un gráfico, necesitas

1. Determinar si es un seno o un coseno desplazado.
2. Mirar la gráfica a la derecha del eje vertical.
3. Encontrar el primer:
   • Pico, si el coeficiente anterior a la función es positivo;
   • Valle, si el coeficiente es negativo.
4. Calcular, la distancia de la recta vertical a ese punto.
5. Si la función era un seno, resta π/2 o 3π/2 a esa distancia para un pico o una depresión, respectivamente.
6. Disfruta de haber hallado el desfase a partir de una gráfica.

Encontrar la amplitud, el periodo y el desfase de una función de la forma A × sen(Bx - C) + D o A × cos(Bx - C) + D es como sigue:

• La amplitud es igual a A;
• El periodo es igual a 2π / B;
• El desfase es igual a C / B.

Para graficar funciones trigonométricas con desplazamiento de fase, necesitas

1. Determinar cuál es la función trigonométrica.
2. Centrarte en el punto (0,0) del plano.
3. Si el desfase es
   • Positivo, muévete a la derecha.
   • Negativo, muévete a la izquierda.
4. Desplázate la distancia dada por el desplazamiento de fase.
5. El punto en el que aterrices es tu punto de partida.
6. Dibuja la gráfica de la función no desfasada como si el punto fuera (0,0).
7. Disfruta de haber representado gráficamente una función trigonométrica con desfase.

Cuando se trata de funciones trigonométricas, sí. Solemos reservar el término “desplazamiento de fase” para las funciones trigonométricas. En otras palabras, podemos tener un desplazamiento horizontal de cualquier gráfica o función. Aun así, cuando se trata, de hecho, de una trigonométrica, podemos llamar equivalentemente a ese desplazamiento horizontal desplazamiento de fase.