Calculadora del área de un sector circular

Con esta calculadora de sectores circulares podrás encontrar rápidamente el área de cualquier sector circular, como, por ejemplo, el área de un semicírculo o de un cuadrante. En este breve artículo:

• Proporcionaremos una definición de sector y explicaremos qué es un sector circular.
• Mostraremos la fórmula del área del sector y explicaremos cómo obtener la ecuación sin mucho esfuerzo.
• Revelaremos algunos ejemplos de la vida real en los que la calculadora sectores circulares puede resultar útil.

Empecemos por la definición de sector: ¿qué es un sector en geometría?

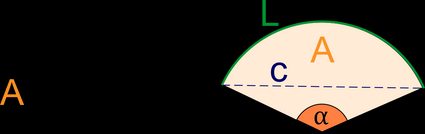
Un sector es una figura geométrica delimitada por dos radios y el arco incluido de una circunferencia.

Los sectores de un círculo se suelen ver en los gráficos circulares o gráficos de pastel, en los que un círculo se divide en varios sectores para mostrar el peso de cada segmento. Las imágenes de abajo muestran algunos ejemplos de sectores circulares; no significa necesariamente que se parezcan a un trozo de tarta, pero por momentos se parecen al resto de la tarta después de haber tomado un trozo:

Puede que en alguna ocasión hayas oído hablar del sector de una elipse, pero las fórmulas son mucho, mucho, más difíciles de utilizar que las ecuaciones del área del sector del círculo.

La fórmula del área del sector es sencilla: multiplica el ángulo central por el radio al cuadrado y divide por 2:

• Área del sector = r² × α / 2

Pero, ¿de dónde sale? Puedes hallarla utilizando proporciones. Todo lo que necesitas recordar es la fórmula del área del círculo (¡y apostamos a que la recuerdas!):

1. El área de un círculo se calcula como A = πr². Este es un buen punto de partida.

2. El ángulo completo es 2π en radianes, o 360° en grados, siendo esta última la unidad angular más común.

3. A continuación, queremos calcular el área de una parte de un círculo, expresada por el ángulo central.

   • Para ángulos de 2π (círculo completo), el área es igual a πr²:

     2π → πr²

   • Entonces, ¿cuál es el área del sector de un círculo?

     α → Área del sector

4. A partir de la proporción, podemos hallar fácilmente la fórmula final del área del sector:

   Área del sector = α × πr² / 2π = α × r² / 2

El mismo método se puede usar para hallar la longitud de arco: solo tienes que recordar la fórmula de la circunferencia de un círculo. Más información en nuestra calculadora de circunferencias y en la calculadora de longitud de arco.

Encontrar el área de un semicírculo o de un cuadrante debería ser ahora pan comido. ¡Solo tienes que pensar qué fracción de un círculo representan!

1. Área de un semicírculo: πr² / 2

• Sabiendo que es la mitad del círculo, divide el área por 2:

  Área de un semicírculo = Área de un círculo / 2 = πr² / 2

• Por supuesto, obtendrás el mismo resultado si utilizas la fórmula del área del sector. Solo tienes que recordar que el ángulo recto es π (180°):

  Área de un semicírculo = α × r² / 2 = πr² / 2

2. Área de un cuadrante: πr² / 4

• Como un cuadrante es un cuarto de círculo, podemos escribir la fórmula como:

  Área de un cuadrante = Área del círculo / 4 = πr² / 4

• El ángulo central del cuadrante es un ángulo recto (π/2 o 90°), por lo que llegarás rápidamente a la misma ecuación:

  Área de un cuadrante = α × r² / 2 = πr² / 4

Lo sabemos, lo sabemos: “¿Por qué tenemos que aprender esto? Nunca jamás lo vamos a utilizar”. Pues bien, nos gustaría demostrarte que la geometría está a nuestro alrededor:

• Si te preguntas qué tamaño de pastel deberías pedir para tu maravillosa fiesta de cumpleaños, ¡bingo, eso es! Usa la fórmula del área de un sector para calcular el tamaño 🍰 correspondiente a cada uno de tus invitados, de modo que nadie se muera de hambre.

• Con la pizza pasa algo parecido: ¿te has dado cuenta de que cada porción es un sector de un círculo 🍕? Por ejemplo, si no te gusta mucho la corteza, puedes calcular qué tamaño de pizza te saldrá mejor.

• ¿Hay aquí algún aficionado a la costura?👗 Los cálculos del área de un sector pueden ser útiles para preparar una falda circular (ya que no siempre es un círculo completo sino, ya sabes, un sector de un círculo en su lugar).

Aparte de esos sencillos ejemplos de la vida real, la fórmula del área del sector puede ser útil en geometría, por ejemplo, para hallar la superficie de un cono.