Calculateur d'arcsin (arc sinus)

Avec ce calculateur d'arcsin (ou calculateur de l'inverse du sinus), vous n'aurez aucun mal à trouver l'arcsin d'un angle. Il vous suffit d'entrer la valeur du sinus, calculée à partir des côtés de votre triangle, et vous trouverez l'angle que vous cherchez. Petit rappel : comme le sinus doit être compris entre -1 et 1, la variable x dans arcsin(x) doit être comprise dans cet intervalle.

Si vous cherchez la définition d'arc sinus ou un graphique représentant la fonction arcsin(x), n'attendez plus ! Faites défiler la page et vous trouverez les réponses ci-dessous. Nous avons également inclus un court paragraphe sur les relations entre la fonction arcsin et d'autres fonctions trigonométriques, ainsi que l'intégrale et la dérivée de l'arc sinus. Alors, qu'attendez-vous ?

L'arc sinus (arcsin) est l'inverse de la fonction sinus. En d'autres termes, elle permet de trouver l'angle dont la valeur du sinus est connue :

arcsin(x) = y si x = sin(y)

Pour obtenir un résultat réel, x doit être compris entre -1 et 1, car il s'agit de la valeur du sinus.

Cependant, vous devriez déjà savoir que la fonction sinus est périodique. Par conséquent, chaque valeur de sinus correspond à plusieurs angles. Par exemple, sin(0) = 0, mais sin(π) est aussi égal à 0, et il en vaut de même pour sin(2π), sin(-π) ou sin(-326π). Donc, il n'y a pas un seul résultat de arcsin(0) : il peut être égal à 2π (360°), à -π (-180°), à 5π (900°) et ainsi de suite ! Toutes ces réponses sont correctes, mais cette calculatrice d'arcsin ne vous donnera que la valeur principale, donc la plus proche de 0 possible.

La notation la plus utilisée de la fonction arc sinus est arcsin(x). Parfois, vous rencontrerez la notation sin^-1x, mais elle peut être confuse avec 1/sin(x). Dans les langages de programmation, on utilise asin(x).

Comme la fonction sinus est périodique, donc plusieurs x correspondent à chaque valeur de y, l'axe des ordonnées de la fonction arc sinus est restreinte : -π/2 ≤ y ≤ π/2. Voilà pourquoi il existe la notion de valeurs principales. En ce qui concerne l'axe des abscisses, elle est restreinte à l'intervalle [-1,1].

Voici un tableau des valeurs de la fonction arcsin les plus courantes :

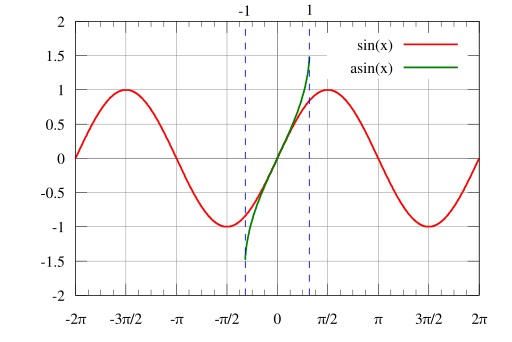
Et voilà le graphique de la fonction arc sinus :

Vous vous demandez d'où vient ce graphique ? Il suffit de restreindre l'axe des abscisses de la fonction sinus à l'intervalle [-π/2 π/2], puis tourner le tout le long de la fonction y = y. L'axe des abscisses devient alors l'axe des ordonnées et vice versa, comme dans l'image ci-dessous.

Mais vous ne devez pas faire tout cela : notre calculatrice d'arcsin fait tout le travaille pour vous !

Les relations entre les fonctions trigonométriques et l'arc sinus peuvent vous aider à mieux comprendre le sujet. Un triangle rectangle dont la longueur l'hypoténuse est égale à 1 est un bon point de départ.

Petit rappel nº 2 : le résultat de la fonction sinus est le rapport entre le côté adjacent opposé à un angle θ et l'hypoténuse : sin(θ) = x / h. L'arc sinus fait exactement l'inverse ; il détermine l'angle à partir du rapport. Donc, si dans notre triangle arcsin(x) = θ, nous pouvons arriver aux conclusions suivantes :

• Sinus : sin(arcsin(x)) = x
• Cosinus : cos(arcsin(x)) = √(1-x²)
• Tangente : tan(arcsin(x)) = x / √(1-x²)

Et même :

• arcsin(x) = π/2 - arccos(x)
• arcsin(-x) = -arcsin(x)

Parfois, l'intégrale et la dérivée de l'arc sinus sont également utiles :

• Intégrale de arcsin(x) : ∫arcsin(x) dx = x arcsin(x) + √(1 - x²) + C

• Dérivée de arcsin(x) : d/dx arcsin(x) = 1 / √(1 - x²)

  où x ≠ -1, 1

L'arc sinus est utilisé, par exemple, pour trouver l'un des angles d'un triangle rectangle. Si vous cherchez les angles d'un triangle rectangle et que vous connaissez la longueur des côtés du triangle, le célèbre théorème de Pythagore ne vous sera pas d'une grande utilité. Pour trouver les angles d'un triangle rectangle, il faut appliquer la fonction arcsin :

• Pour α : sin(α) = a / c donc α = arcsin(a / c)
• Pour β : sin(β) = b / c donc β = arcsin(b / c)

Disons que nous voulons trouver l'angle α étant donné l'hypoténuse c = 10 et le côté adjacent opposé à α, a = 6.

1. Insérez la valeur dont vous voulez trouver l'arc sinus. Vous pouvez saisir 6/10 ou 0,6, cela ne change rien. N'oubliez pas que cette valeur doit être comprise entre -1 et 1.
2. Et... le tour est joué ! Le calculateur d'arcsin a fait son travail et vous avez trouvé l'arc sinus de votre valeur. Vous savez maintenant que arcsin(6/10) = 36,87°.