Calculateur de trigonométrie
Sommaire
Qu'est-ce que la trigonométrie ?Utiliser le calculateur de trigonométrie pour trouver sin, cos, tan, cotan, sec, cosecCalculateur de trigonométrie comme outil de résolution de triangles rectanglesFAQCe calculateur de trigonométrie vous aidera essentiellement pour deux cas courants où la trigonométrie est nécessaire. Si vous souhaitez trouver les valeurs du sinus, du cosinus, de la tangente, ainsi que de leurs fonctions réciproques, utilisez la première partie du calculateur. Cherchez-vous le côté ou l'angle manquant dans un triangle rectangle ? Voulez-vous les trouver à l'aide de la trigonométrie ? Notre outil est également une valeur sûre ! Saisissez 2 ou 3 valeurs que vous connaissez dans la deuxième partie du calculateur, et vous trouverez la réponse en un clin d'œil. Continuez à lire si vous souhaitez en savoir plus sur la trigonométrie et sur les domaines dans lesquels vous pouvez l'appliquer.
Il existe de nombreux autres outils mathématiques qui permettent de résoudre les problèmes de trigonométrie. Découvrez deux lois trigonométriques répandues avec le calculateur de la loi des sinus 🇺🇸 et le calculateur de la loi des cosinus 🇺🇸, qui vous aideront à résoudre n'importe quel type de triangle.
Qu'est-ce que la trigonométrie ?
La trigonométrie est une branche des mathématiques. Son nom vient du grec trigōnon, triangle, et metron, mesure. Nous pouvons donc en déduire que la trigonométrie traite principalement des angles et des triangles. En particulier, elle définit et utilise les relations et les rapports entre les angles et les côtés des triangles. Ainsi, elle est surtout utilisée pour résoudre des triangles, des triangles rectangles plus précisément, mais aussi tout autre type de triangle que vous souhaitez.
🔎 Les fonctions trigonométriques (sin, cos, tan) représentent toutes des rapports. Par conséquent, vous pouvez trouver vos valeurs manquantes en utilisant uniquement notre calculateur de ratio !
La trigonométrie a une multitude d'applications : de l'astronomie à la géographie, en passant par le système de navigation par satellite et les problèmes de la vie quotidienne, tels que le calcul de la hauteur ou de la distance entre des objets. En outre, les fonctions sinus et cosinus sont fondamentales pour décrire les phénomènes périodiques : grâce à elles, nous pouvons décrire des ondes, telles que le son, les vibrations ou la lumière, ainsi que des mouvements oscillatoires. Vous pouvez en découvrir plus à propos de ceux-derniers sur notre calculateur de pendule simple.
De nombreux domaines de la science et de l'ingénierie utilisent la trigonométrie et les fonctions trigonométriques, à savoir : la musique, l'acoustique, l'électronique, la médecine et l'imagerie médicale, la biologie, la chimie, la météorologie, l'ingénierie électrique, mécanique et civile, et même l'économie... Les fonctions trigonométriques sont vraiment partout autour de nous !
Utiliser le calculateur de trigonométrie pour trouver sin, cos, tan, cotan, sec, cosec
Pour trouver les fonctions trigonométriques d'un angle, entrez l'angle choisi en degrés ou en radians. Les six fonctions trigonométriques les plus courantes s'afficheront sous le calculateur. Vous verrez trois fonctions de base (sinus, cosinus et tangente), ainsi que leurs fonctions réciproques (cosécante, sécante et cotangente). En outre, si l'angle est aigu, vous verrez également le triangle rectangle en question, ce qui vous aidera à comprendre comment les fonctions peuvent être interprétées.
Calculateur de trigonométrie comme outil de résolution de triangles rectangles
Pour trouver les côtés ou les angles manquants d'un triangle rectangle, il vous suffit de saisir les variables connues dans le calculateur de trigonométrie. Vous n'avez besoin que de deux valeurs si vous connaissez :
- un côté et un angle ;
- deux côtés ; ou
- l'aire et un côté.
Rappelez-vous que si vous ne connaissez que deux angles, cela ne suffit pas pour trouver les côtés du triangle. Les côtés de deux triangles ayant les mêmes angles, et donc la même forme, peuvent avoir des longueurs différentes. Ce type de relation s'appelle la similitude des triangles. Si les côtés ont la même longueur, les triangles sont congruents.
Qu'est-ce que la trigonométrie ?
La trigonométrie est l'étude des rapports d'un triangle. Pour les triangles rectangles, le rapport entre deux côtés est toujours le même, et il est donné par les fonctions trigonométriques cos, sin et tan. La trigonométrie peut également aider à trouver certaines informations manquantes, comme les côtés ou les angles d'un triangle, qui peuvent être calculés à l'aide de la loi des sinus, par exemple.
Comment faire de la trigonométrie ?
- Trouvez deux mesures parmi l'hypoténuse, l'un des angles, le côté adjacent et le côté opposé.
- Déterminez quels éléments restants, vous essayez de calculer.
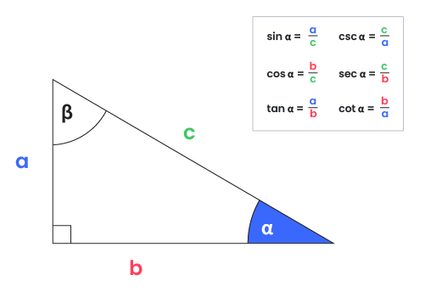
- Choisissez la fonction dont vous avez besoin. Rappelez-vous de la règle mnémotechnique SOHCAHTOA.
- Remplissez l'équation avec les données dont vous disposez.
- Réorganisez les termes de l'équation et résolvez l'inconnue.
- Vérifiez vos réponses à l'aide de notre calculateur de trigonométrie.
La trigonométrie est-elle difficile ?
La trigonométrie peut être difficile au début, mais après un peu de pratique, vous la maîtriserez ! Voici quelques conseils de trigonométrie :
- Marquez l'hypoténuse, les côtés adjacents et les côtés opposés de votre triangle pour vous aider à déterminer la fonction à utiliser.
- N'oubliez pas la règle mnémotechnique SOHCAHTOA pour les relations trigonométriques !
À quoi sert la trigonométrie ?
La trigonométrie est utilisée pour trouver des informations sur les triangles, et sur les triangles rectangles en particulier. Les triangles étant omniprésents dans la nature, la trigonométrie est utilisée en dehors des mathématiques, dans des domaines, tels que la construction, la physique, l'ingénierie chimique et l'astronomie.
Qui a inventé la trigonométrie ?
La trigonométrie étant la relation entre les angles et les côtés d'un triangle, personne ne l'a inventée. En effet, elle existerait toujours même si personne ne la connaissait ! Les premières personnes à avoir découvert une partie de la trigonométrie étaient les anciens Égyptiens et Babyloniens, mais Euclide et Archimède ont été les premiers à prouver les identités trigonométriques, bien qu'ils l'aient fait en utilisant des formes, et non de l'algèbre.
À partir de quelle classe la trigonométrie est-elle enseignée ?
En France, en Belgique et au Québec, la trigonométrie est enseignée à partir de la 3ᵉ, c'est-à-dire de l'âge de 13-14 ans. L'âge exact auquel la trigonométrie est enseignée dépend du pays, de l'école et des capacités des élèves.
Comment convertir les nombres décimaux en degrés en trigonométrie ?
- Trouvez la relation trigonométrique que vous utilisez à l'aide de la règle mnémotechnique SOHCAHTOA.
- Prenez l'identité réciproque de votre nombre décimal, par exemple sin⁻¹(0,5).
- Le résultat est la mesure en degrés de votre angle.
- Vérifiez vos résultats avec notre calculateur de trigonométrie.
Comment trouver la hauteur d'un triangle en utilisant la trigonométrie ?
- Dessinez votre triangle et marquez la hauteur. Vous devrez diviser le triangle en deux triangles plus petits.
- Résolvez l'un ou l'autre de ces triangles restants en utilisant la trigonométrie classique pour trouver la hauteur. L'opposé ou l'adjacent sera maintenant l'hypoténuse du plus petit triangle.
- Vérifiez vos réponses à l'aide du calculateur Omni.
