Calculateur de factorielle

Bienvenue sur le calculateur de factorielle : un outil qui calcule la factorielle de n'importe quel nombre de 0 à 170. En plus de calculer, par exemple, la factorielle de 0 ou la factorielle de 5. Nous vous montrerons également comment utiliser le point d'exclamation en mathématiques, nous vous informerons sur la formule de la factorielle de n'importe quel nombre et sur les applications qu'elle peut avoir. À la fin de ce cours, vous aurez une réponse à la question « Qu'est-ce qu'une factorielle ? » en utilisant la définition de la factorielle. Enfin, nous nous plongerons dans les mathématiques sous-jacentes pour découvrir comment nous pouvons inclure plus que des entiers positifs en utilisant la fonction gamma.

Lorsque vous avez vu un point d'exclamation en mathématiques pour la première fois, vous avez probablement été choqué·e et vous avez même pensé qu'il s'agissait d'une erreur ou d'une faute de frappe. Mais la réalité est tout autre : ce point d'exclamation en maths s'appelle la factorielle. La factorielle est un opérateur relativement peu connu qui peut, en fait, être considéré davantage comme une abréviation que comme un véritable opérateur, du moins au début.

Il est important de ne pas confondre la factorielle avec la factorisation des nombres premiers d'un nombre, qui, comme son nom l'indique, permet d'obtenir les nombres premiers qui, multipliés ensemble, donnent votre nombre. La factorisation des nombres premiers a son utilité en mathématiques et est sans doute plus connue que le calcul de la factorielle. La popularité de la factorisation des nombres premiers s'explique en partie par son utilité dans le calcul du plus grand commun diviseur (PGCD) et du plus petit commun multiple (PPCM), mais nous nous éloignons du sujet. Toutefois, vous trouverez de plus amples informations avec notre calculateur de factorisation des nombres premiers 🇺🇸.

Pour comprendre ce qu'est le calcul de la factorielle, commençons par un exemple. Nous pourrions choisir n'importe quel nombre n et calculer sa factorielle, mais il est préférable de choisir un nombre relativement petit, alors utilisons la factorielle de 5.

5! = 5 × 4 × 3 × 2 × 1 = 120

Cela vous montre que ce n'est pas sorcier, et vous pourriez même deviner la formule de la factorielle à partir de cet exemple. Vous pouvez également comprendre pourquoi ce point d'exclamation en mathématiques peut être considéré comme une abréviation puisqu'il ne s'agit pas d'une nouvelle opération, mais plutôt d'un ensemble de multiplications. En bref, et de manière quelque peu informelle, nous pouvons définir la factorielle comme la multiplication de tous les nombres entiers positifs inférieurs et égaux au nombre entier donné.

En jouant un peu avec cela, nous pouvons voir que pour la factorielle de 5, nous pouvons le relier à la factorielle de 4 d'une manière directe :

5! = 5 × (4 × 3 × 2 × 1) = 5 × 4!

Ce type de relation entre des factorielles de différents n est à la base de la formule mathématique qui définit l'opération factorielle, comme nous le verrons dans la section suivante.

L'opération factorielle n'est pas utilisée partout en mathématiques, mais elle est essentielle dans les statistiques et les problèmes de probabilité. Dans ces cas, en particulier lorsqu'il s'agit de permutations ou de combinaisons, la factorielle apparaît presque tout le temps. Dans les sections suivantes de notre calculateur de factorielle, nous verrons des exemples de problèmes qui nécessitent l'utilisation de factorielles et de la formule de calcul de la factorielle.

Jusqu'à présent, nous avons vu une réponse un peu vague à la question « Qu'est-ce qu'une factorielle ? », mais nous n'avons pas donné de définition factorielle correcte. C'est précisément l'objectif de cette section : voir et expliquer la formule factorielle et la façon dont nous pouvons trouver la définition factorielle d'une manière plus mathématique à partir de cette formule.

Pour une description plus mathématique de la formule factorielle, examinons la factorielle d'un certain n et sa relation avec les autres factorielles. Dans ce cas, n peut être n'importe quel nombre. Si nous regardons les exemples précédents avec la factorielle de 5, nous pouvons voir que :

5! = 5 × 4 ! = 5 × (5-1)!

Si nous extrapolons maintenant ce résultat à la factorielle de n :

n! = n × (n-1)!

La formule ci-dessus est la formule générale de la factorielle et fait partie intégrante de la définition de la factorielle. Cependant, nous sommes certains que cela ne répond pas à toutes les questions que vous pouvez vous poser sur les factorielles. Par exemple, que se passerait-il si nous prenions un nombre négatif ? Quand doit-on arrêter de soustraire des nombres ? Ce sont des questions valables auxquelles la formule de la factorielle ci-dessus ne répond pas, mais qui sont fondamentales pour obtenir une définition correcte de la factorielle.

On peut répondre facilement à ces deux questions en affirmant que la formule factorielle est uniquement définie pour les entiers positifs, ce qui signifie qu'on ne peut pas descendre en dessous de n = 1. Mais cela soulève une autre question : qu'est-ce que la factorielle de 0 ? Puisque nous ne pouvons pas utiliser cette formule, vous êtes en droit de penser que cette question n'a pas de réponse et que toute cette histoire de factorielle est fausse. Cependant, il existe une « astuce » pour contourner ce problème : en fixant la valeur de la factorielle de zéro à un nombre par définition.

C'est ainsi que nous arrivons à la convention :

0! = 1

Un petit avertissement est nécessaire ici, car, en mathématiques, les choses ne sont jamais aussi simples. Il y a beaucoup de raisons complexes pour lesquelles la valeur de la factorielle de zéro est égale à un et non à un autre nombre. Cependant, expliquer ces raisons en détail dépasse largement le cadre de ce calculateur de factorielle.

Vérifions maintenant quelques valeurs de la factorielle de plusieurs petits n, comme la factorielle de 0, la factorielle de 3, la factorielle de 5. Portez une attention particulière à la valeur de la factorielle de 0, car c'est la plus importante, et nous en parlerons plus tard.

• 0! = 1
• 1! = 1
• 2! = 2
• 3! = 6
• 4! = 24
• 5! = 120
• 6! = 720
• 7! = 5 040
• 8! = 40 320
• 9! = 362 880
• 10! = 3 628 800

Nous pouvons voir à quelle vitesse la factorielle d'un nombre augmente au fur et à mesure que nous utilisons des nombres plus grands. Il s'agit d'une autre situation où la notation scientifique peut vous sauver la mise (si vous savez comment tronquer correctement les chiffres significatifs nécessaires) lorsque vous devez travailler avec des nombres aussi grands. Pour les factorielles de nombres supérieurs à 10, n'hésitez pas à utiliser le calculateur de factorielle ci-dessus. Par ailleurs, vous pouvez utiliser les logarithmes pour calculer les factorielles de nombres plus élevés. Pour voir comment faire, vous pouvez consulter notre calculateur de logarithme où nous expliquons comment le logarithme peut être appliqué pour ce type de calculs arithmétiques.

La factorielle de 0 est un élément clé de la définition factorielle. Pour comprendre pourquoi elle est si importante, nous pouvons montrer les problèmes que nous rencontrons lorsque nous essayons de la calculer en utilisant la formule de factorielle ci-dessus :

0! = 0 × (0-1)!

Il semble que quelle que soit la valeur de (0-1)!, le résultat devrait toujours être 0! = 0, mais les choses sont plus compliquées que cela en mathématiques. Dans la section précédente, nous avons vu que la factorielle de n n'est défini que pour n > 0, ce qui pose un problème. Le terme (0-1)! est ce que les mathématiciens appellent : une expression non définie, ce qui signifie que l'expression n'est pas correcte et qu'elle n'a donc aucune signification mathématique. Le problème est le même que pour la division par zéro. Le problème n'est pas qu'on ne peut pas la calculer. Le problème est que l'expression n'a pas de sens, elle n'a pas de signification.

C'est la raison pour laquelle il est essentiel de définir 0! comme une valeur de convention. Fixer sa valeur à 0! = 0 ne serait pas une bonne idée, car cela signifierait que n! = 0 pour toute valeur de n. Vous pouvez voir pourquoi en appliquant la formule factorielle. À mainte reprise, si nous avons fixé la factorielle de zéro à 1, nous retrouvons les valeurs attendues pour le facteur n tout en ayant une convention simple pour la valeur de 0!.

Dans la section suivante, nous verrons une autre raison pour fixer la factorielle de zéro à 1, avec un peu plus de logique mathématique derrière cela. Ce faisant, nous introduirons également la fonction Gamma, qui est, en termes simples, une formule factorielle étendue qui inclut tous les nombres positifs et le facteur 0.

Il est possible de déterminer la factorielle des nombres non entiers ; en fait, c'est possible pour tous les nombres réels et complexes, à l'exclusion des entiers négatifs. Cette méthode nécessite l'utilisation d'outils mathématiques sophistiqués, c'est pourquoi nous essaierons d'en donner ici une version simplifiée, en conservant autant d'exactitude que possible. Plusieurs approches ont été adoptées pour étendre la formule de la factorielle à tous les nombres positifs, chacune avec des différences subtiles et pour la plupart compatibles entre elles.

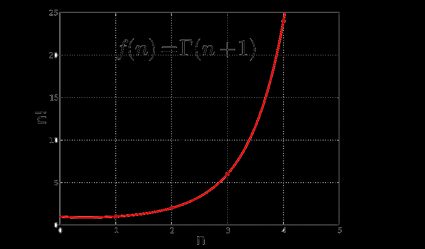
Commençons par la fonction Gamma. La fonction Gamma est une fonction qui étend la notion de la factorielle de n au-delà des entiers. Évidemment, la formule ne peut pas être la même que celle que nous avons utilisée précédemment, car nous nous retrouverions dans une impasse. En fait, cette fonction étend la notion de factorielle de n aux nombres complexes, où la notion intuitive de factorielle est beaucoup plus difficile à saisir. Les seuls nombres pour lesquels la fonction Gamma n'est pas définie sont les entiers négatifs :

𝚪(z) = ∫tᶻ⁻¹ e⁻ᵗ dt

C'est la définition de la fonction Gamma, où t est la variable d'intégration de zéro vers l'infini, et z est un nombre entier non négatif. Cette formule se réduit à la formule de la factorielle lorsqu'elle est appliquée à tout entier positif n.

n! = 𝚪(n+1)

Vous pouvez constater deux choses à partir de cette formule :

1. La fonction Gamma est beaucoup plus compliquée à utiliser que la formule de la factorielle pour les entiers.
2. Ce n'est pas une copie exacte de la factorielle puisque vous devez calculer la valeur de la fonction Gamma pour n+1 pour obtenir n!.

Pour remédier au second problème, nous pouvons introduire la fonction Pi.

𝚷(z) = ∫tᶻ e⁻ᵗ dt

La fonction Pi est très similaire à la fonction Gamma, mais décalée juste assez pour que la factorielle et la fonction correspondent.

𝚷(n) = n!, n ∈ 𝗡

Vous pourriez être déconcerté·e par la complexité des mathématiques qui se cachent derrière cette formule de la factorielle, mais ne vous inquiétez pas ! En guise d'astuce, nous pouvons vous dire que (-0,5) ! = √π et (0,5) ! = 0,5√π.

Il est intéressant de noter que la première formule de la factorielle reste valable ici. Ainsi, par exemple :

(2,5) ! = 2,5 × (1,5) ! = 2,5 × 1,5 × (0,5) ! = 1,875√π

Nous avons déjà évoqué le fait que la factorielle est couramment utilisée dans les calculs probabilistes ou les permutations, mais ce n'est pas tout. Voyons les autres champs où la factorielle de n apparaît. En restant dans le domaine des mathématiques pures, nous arrivons à la loi binomiale qui permet de calculer les probabilités, par exemple, que des expériences indépendantes aient des résultats similaires.

Outre les mathématiques, la factorielle de n apparaît dans de nombreux autres calculs, notamment en physique statistique et en physique des particules, qui sont des champs de la physique qui traitent des permutations de particules, entre autres choses. En particulier, la physique statistique est un domaine de la physique qui peut être considérée comme une version microscopique de la thermodynamique. En effet, la physique statistique traite des problèmes de thermodynamique (tout comme notre calculateur d'enthalpie de changement d'état 🇺🇸), mais elle le fait particule par particule.

Il existe d'autres domaines (principalement en physique) qui utilisent les factorielles dans les calculs, et nous pourrions approfondir la question de savoir comment et pourquoi ils utilisent la formule de factorielle dans leurs calculs. Cependant, pour un simple calculateur comme celui-ci, cela serait bien au-delà de sa portée.

Dans notre monde moderne, les calculs fastidieux sont généralement laissés aux ordinateurs (comme vous le faites en utilisant ce calculateur de factorielle). L'utilisation de langages informatiques pour créer de petits programmes qui feront ces calculs à notre place est de plus en plus courante. La factorielle est une candidate parfaite puisqu'elle n'est pas vraiment complexe d'un point de vue conceptuel. Cependant, le calcul d'un grand nombre de nombres nécessite trop de temps pour les humains. Pour ceux qui utilisent des langages de programmation, nous allons laisser quelques exemples pour certains des langages de codage les plus courants.

• Factorielle en Python (après 2,6) : utilisez math.factorial(x) pour obtenir les valeurs factorielles en Python.

• Factorielle en Java : il n'y a pas de méthode Java factorial dans les bibliothèques Java standard.

• Factorielle avec Matlab : pour calculer une factorielle, Matlab utilise factorial(x). Vous trouverez plus d'informations sur la fonction factorielle avec Matlab dans la documentation officielle.

• Factorielle dans Excel : utilisez FACT pour calculer la factorielle dans Excel. Notez que la factorielle dans Excel ne fonctionne qu'avec des nombres entiers.

• Factorielle en C++ : il n'y a pas de fonction factorielle en C++ incluse dans les bibliothèques standard. Regardez ici un exemple de fonction factorielle en C++.

• Factorielle en Javascript : il n'y a pas de fonction factorielle en Javascript incluse dans les bibliothèques standard.