Calculateur de fonction affine

Ce calculateur de fonction affine vous aidera à trouver l'équation d'une droite à partir de deux points. Il vous aidera à trouver le coefficient directeur et l'ordonnée à l'origine, ainsi que l'abscisse à l'origine. Pour en savoir plus sur les fonctions affines, l'équation d'une droite et leurs applications dans la vie réelle, lisez la suite.

Toute droite sur un plan peut être représentée mathématiquement par une fonction qui lie les positions verticales (axe des abscisses) et horizontales (axe des ordonnées) de ses points. Cette fonction peut être écrite sous la forme y = [quelque chose de x], où [quelque chose de x] est une expression qui dépend de la valeur de x et détermine la représentation graphique de notre fonction. Par exemple, y = x² + x est une parabole, aussi appelée fonction quadratique. En revanche, y = mx + b (avec m et b représentant des nombres réels quelconques) est une droite.

Ce calculateur de fonction affine détermine seulement les équations linéaires, c'est-à-dire les équations de droite. Vous pouvez consulter notre calculateur de taux de variation moyen 🇺🇸 si vous souhaitez en savoir plus sur les variables des équations non linéaires.

Les équations linéaires ne contiennent pas de termes avec des exposants. (Par exemple, vous trouverez un x ou un y, mais jamais un x².) Chaque équation linéaire décrit une ligne droite, qui peut être exprimée à l'aide de l'expression algébrique des fonctions affines.

Comme nous l'avons vu précédemment, vous pouvez écrire l'équation de n'importe quelle droite sous la forme y = mx + b, où m est le coefficient directeur (aussi appelé pente) et b son ordonnée à l'origine b. Vous pouvez utiliser ces mêmes valeurs pour effectuer une interpolation linéaire.

Le coefficient directeur ou pente désigne l'inclinaison ou le gradient d'une droite. Il nous indique la variation de y par rapport à une variation de x donnée. S'il est positif, les valeurs de y augmentent lorsque x augmente. S'il est négatif, y diminue lorsque x augmente. Vous pouvez approfondir vos connaissances grâce à notre calculateur de pente.

L'ordonnée à l'origine est la valeur de y à laquelle la droite coupe l'axe des ordonnées. Pour la trouver, vous devez remplacer x par 0 dans l'équation linéaire. Vous verrez plus tard pourquoi l'ordonnée à l'origine est un paramètre important dans les équations linéaires, et vous apprendrez également la signification physique de sa valeur dans certains exemples du monde réel.

Vous ne savez toujours pas comment trouver l'équation d'une fonction affine ? Nous allons supposer que vous connaissez deux points par lesquels passe la droite. Le premier aura pour coordonnées (x₁, y₁) et le second (x₂, y₂). Vos inconnues sont le coefficient directeur m et l'ordonnée à l'origine b.

Tout d'abord, remplacez les coordonnées des deux points à la place des y et x dans les équations suivantes :

(1) y₁ = mx₁ + b

(2) y₂ = mx₂ + b

Soustrayez ensuite la première équation de la seconde :

y₂ - y₁ = m(x₂ - x₁)

Enfin, divisez les deux côtés de l'équation par (x₂ - x₁) pour trouver le coefficient directeur :

m = (y₂ - y₁)/(x₂ - x₁)

Une fois que vous avez trouvé le coefficient directeur, vous pouvez remplacer m par (y₂ - y₁)/(x₂ - x₁) dans la première ou la deuxième équation pour trouver l'ordonnée à l'origine :

y₁ = x₁(y₂ - y₁)/(x₂ - x₁) + b

b = y₁ - x₁(y₂ - y₁)/(x₂ - x₁)

Ce calculateur de fonction affine vous permet de trouver l'équation d'une droite de la forme y = mx + b. Vous avez juste à saisir deux points par lesquels la droite passe et suivre les instructions ci-dessous :

1. Notez les coordonnées du premier point. Prenons : x₁ = 1 et y₁ = 1.

2. Notez les coordonnées du deuxième point. Prenons : x₂ = 2 et y₂ = 3.

3. Utilisez la formule du coefficient directeur pour trouver m :

   m = (y₂ - y₁)/(x₂ - x₁) = (3-1)/(2-1) = 2/1 = 2.

4. Calculez l'ordonnée à l'origine. Vous pouvez également utiliser x₂ et y₂ au lieu de x₁ et y₁.

   b = y₁ - m × x₁ = 1 - 2×1 = -1

5. Rassemblez toutes ces valeurs pour construire l'équation de notre fonction affine :

   y = 2x - 1.

6. Vous pouvez également utiliser le calculateur de distance pour trouver la distance entre deux points.

Il est toujours possible de trouver l'abscisse à l'origine d'une droite. Il s'agit de la valeur de x à laquelle la droite coupe l'axe des abscisses (c'est-à-dire la valeur de x pour laquelle y est égal à 0). Vous pouvez la calculer de la manière suivante :

0 = mx + b

x = -b/m

La seule condition est que le coefficient m soit différent de zéro.

Notre calculateur de fonction affine affichera pour vous les valeurs de l'ordonnée et de l'abscisse à l'origine. Toutefois, si vous souhaitez en savoir plus à leur sujet, nous vous recommandons de consulter notre calculateur d'abscisse et d'ordonnée à l'origine 🇺🇸.

Nous connaissons désormais l'expression algébrique d'une fonction affine. Pour comprendre pourquoi cette expression est si utile, il est important de voir comment elle peut être appliquée au monde réel. Voyons ensemble quelques exemples. Nous commencerons par des exemples simples tirés de la physique. Cela nous aidera à comprendre la signification de l'ordonnée à l'origine et de l'abscisse à l'origine.

Imaginez une voiture qui se rapproche de vous à vitesse constante. Son mouvement peut être représenté par un graphique de la distance entre la voiture et vous en fonction du temps (comme indiqué ci-dessus). Cela signifie que l'axe des abscisses représente le temps écoulé et l'axe des ordonnées la distance qui vous sépare de la voiture. Vous pouvez même imaginer que la voiture a commencé à se déplacer avant que vous ne déclenchiez le chronomètre (c'est-à-dire avant t = 0).

Maintenant, regardez l'ordonnée à l'origine (x = 0). C'est le point à partir duquel vous avez commencé à mesurer le temps, donc ici t = 0. Ainsi, la valeur de y à ce point indiquera la position de départ (distance) de la voiture par rapport à vous. Cette valeur est, comme nous l'avons vu précédemment, la même que la valeur de b dans l'équation d'une fonction affine.

Maintenant, regardez l'abscisse à l'origine (y = 0). Il s'agit du point où la distance entre la voiture et vous est égale à 0. La valeur de x à ce point sera donc le moment où vous et la voiture étiez au même endroit. Espérons que cela signifie que vous étiez à l'intérieur de la voiture et non en dessous.

L'exemple de la voiture ci-dessus est très simple et devrait vous aider à comprendre l'importance de la forme affine d'une équation, et en particulier, celle des points d'intersection avec les axes. Cet article se concentre sur les fonctions affines et donc les lignes droites, mais les points d'intersections peuvent être calculés pour n'importe quel type de courbe (si elle traverse un axe).

L'exemple ci-dessus ne correspond pas à une équation linéaire. Néanmoins, la courbe coupe l'axe des ordonnées et l'axe des abscisses ; on pourrait donc trouver les coordonnées de ses points d'intersection. Il en va de même pour toute autre parabole ou autre forme.

La parabole est une équation dont l'ordonnée à l'origine est garantie, mais qui n'a pas nécessairement d'abscisse à l'origine. Elle présente un maximum ou un minimum (selon l'orientation). Le graphique ci-dessus illustre une parabole avec un minimum. Si le maximum est en dessous de l'axe des abscisses ou si le minimum est au-dessus de l'axe des abscisses, il n'y aura jamais d'abscisse à l'origine.

Cependant, toutes les équations ne se valent pas. Certaines formules décrivent des courbes qui ne coupent ni l'axe des abscisses, ni l'axe des ordonnées, et même parfois aucun des deux. Voyons un peu plus en détail comment cela est possible.

On peut distinguer trois groupes d'équations selon le nombre de points d'intersection avec les axes : les équations avec des ordonnées à l'origine seulement, celles avec seulement des abscisses à l'origine et les équations sans intersection. Le premier groupe (ordonnées à l'origine seulement) contient les équations qui coupent l'axe des ordonnées, mais pas l'axe des abscisses. Ce groupe comprend une grande variété d'équations, y compris les équations linéaires. Par exemple, l'équation y = 3 est une droite parallèle à l'axe des abscisses, et elle n'a donc pas d'intersection avec cet axe. N'essayez pas de calculer ce genre d'intersection sur ce calculateur de fonction affine, car ces équations peuvent apparemment casser Internet.

Les deuxième et troisième groupes d'équations sont un peu plus difficiles à imaginer et pour bien les comprendre, nous devons introduire le concept d'asymptote. Une asymptote est une droite (qui peut être exprimée sous la forme d'une équation linéaire) dont la fonction ou la courbe dont nous parlons s'en rapproche de plus en plus, sans jamais la couper ou la toucher.

Illustrons cette définition par un exemple afin de rendre le concept d'asymptote un peu plus concret. Prenons l'équation y = 1/x. Si nous essayons de trouver l'ordonnée à l'origine en remplaçant x = 0, nous obtenons ce qu'on appelle en mathématiques une forme indéterminée puisque diviser par 0 n'a pas sens.

Si nous prenons des valeurs de plus en plus proches de 0 (comme 0,1, puis 0,001, 0,000 001, ...), nous pouvons voir que la valeur de y augmente très rapidement. Ainsi, autour du point x = 0, nous savons que y aurait une très grande valeur, mais du fait des règles mathématiques, il n'y a pas de valeur définie pour ce point précis. On écrit parfois 1/0 = ∞, mais en réalité, l'infini n'est pas un nombre mais un concept.

Dans ce cas, l'équation linéaire x = 0 représente l'asymptote de la fonction y = 1/x. Cela signifie que y = 1/x ne coupera jamais cette droite et n'aura donc pas d'ordonnée à l'origine. En général, chaque fois qu'une fonction a une asymptote qui se trouve sur l'un des axes, il lui manquera au moins un des points d'intersection.

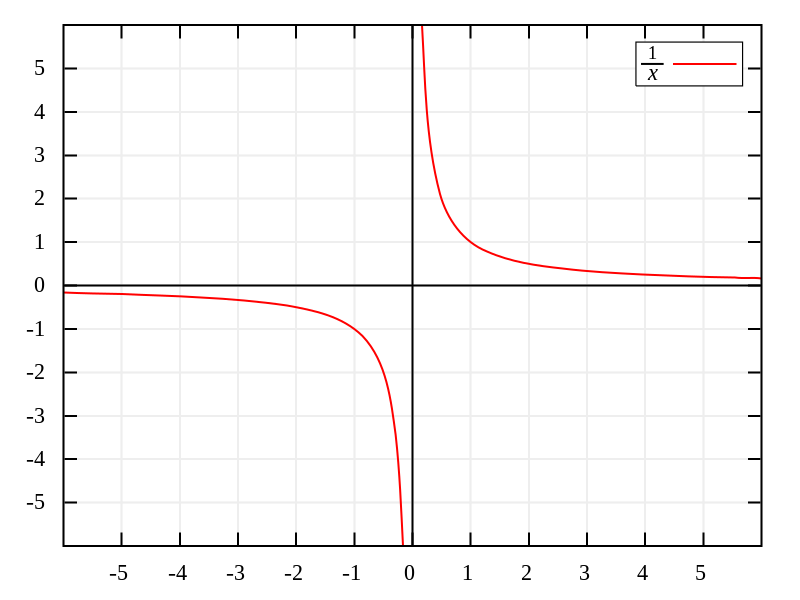
En fait, l'exemple que nous vous avons montré (y = 1/x) a aussi une asymptote pour y = 0, c'est-à-dire l'axe des abscisses. Pour la même raison que précédemment, y = 0 n'est jamais défini car il faudrait x = ∞, et comme on le sait, désormais, c'est impossible puisque l'infini est un concept et non un nombre.

Avant de passer au sujet suivant, il est important de noter que nous avons fait une présentation très simplifiée de la notion d'infini. Cette approche est suffisante pour ceux qui ne sont pas familiers avec l'infini en mathématiques, mais elle ne couvre pas toutes les subtilités de la notion. Si vous souhaitez en savoir plus sur l'infini, nous vous recommandons de commencer par les formes indéterminées en mathématiques.

On pourrait facilement penser que l'utilité des équations linéaires est très limitée en raison de leur simplicité. Cependant, la réalité est un peu différente. Les équations linéaires sont au cœur de certaines des méthodes les plus puissantes pour résoudre les problèmes de minimisation et d'optimisation.

Les problèmes de minimisation sont un type de problème dans lequel on cherche à rendre l'une des variables aussi petite que possible. Cette variable peut être, par exemple, la différence entre une prédiction faite par un modèle et la réalité. Ce type de problème est l'un des problèmes les plus courants et est au cœur du machine learning (apprentissage automatique) et des expériences scientifiques.

Pour trouver la valeur minimale d'une équation ou d'une formule, on utilise la très connue méthode de Newton, nommée d'après le génie qui l'a inventée. Cette méthode utilise les dérivées, les équations linéaires et les ordonnées à l'origine :

Cette méthode consiste à choisir une valeur pour x et à calculer la dérivée de l'équation en ce point. On peut ensuite utiliser la dérivée comme la pente d'une équation linéaire qui passe par ce point (x,y). L'ordonnée à l'origine de cette équation linéaire peut être calculée à partir de la dérivée.

Une fois l'ordonnée à l'origine calculée, cette valeur de x est utilisée pour répéter le processus ci-dessus, un certain nombre de fois. On continue à répéter le processus jusqu'à ce que nous arrivions à une valeur de y qui soit la plus petite possible (ce qui signifie que la dérivée sera égale à 0). Dans la vie réelle, arriver au point minimal exact n'est pas possible en un temps fini. On se contente typiquement d'une valeur « assez proche ».

Un exemple très courant est l'utilisation de la méthode des moindres carrés pour ajuster des données à une formule ou à une tendance. Dans ce cas, la valeur que nous voulons minimiser est la somme des carrés de la distance entre la ligne de tendance et les points de données. La distance est calculée le long d'une ligne perpendiculaire entre le point et la ligne de tendance.

Non, l'équation cartésienne et l'équation d'une fonction affine sont deux façons différentes de décrire une droite.

• La fonction affine se lit y = mx + b, où m est le coefficient directeur (pente) de la droite, et b est l'ordonnée à l'origine, c'est-à-dire la valeur à laquelle la droite coupe l'axe des ordonnées. Par exemple, y = -2x + 3.
• L'équation cartésienne se lit Ax + By + C = 0, où A, B, C sont des nombres entiers. Par exemple, 2x + y - 3 = 0.

Si vous souhaitez réécrire votre équation cartésienne sous la forme d'une fonction affine, procédez comme suit :

1. Écrivez l'équation cartésienne de votre droite : Ax + By + C = 0.
2. Déplacez Ax et C de l'autre côté du signe égal tel que : By = -Ax - C.
3. Divisez les deux côtés par B : y = -(A/B)x - (C/B).
4. Comme vous pouvez le voir, nous obtenons une fonction affine : y = mx + b avec le coefficient directeur m = -A/B et l'ordonnée à l'origine b = -C/B.

La pente (ou coefficient directeur) décrit l'inclinaison d'une droite. La pente peut être positive, négative ou nulle.

• Une pente positive signifie que la droite monte de gauche à droite.
• Une pente négative signifie que la droite descend de gauche à droite.
• Une pente nulle signifie que la droite est horizontale.

Plus la valeur absolue de la pente est grande, plus la droite augmente ou diminue rapidement. En fait, la valeur de la pente est exactement l'augmentation ou la diminution de la droite lorsque x augmente d'une unité.

La pente est m = 1. Pour obtenir ce résultat, utilisez la formule m = tan(α), où α est l'angle entre la droite et l'axe des abscisses. Puisque tan(45°) = 1, nous obtenons la pente égale à 1, comme indiqué ci-dessus.