Calculateur de produit vectoriel

Sans calculateur de produit vectoriel, difficile de savoir comment calculer le produit vectoriel. Heureusement pour vous, nous avons créé un outil qui vous aide à comprendre la formule du produit vectoriel de deux vecteurs. Nous allons également comparer les définitions du produit scalaire et du produit vectoriel et vous expliquer pourquoi il ne s'agit pas de la même opération. Et en bonus, nous avons aussi une liste de conseils pratiques comme la règle de la main droite afin que vous puissiez devenir un maître dans l'art d'effectuer le produit vectoriel de deux vecteurs.

Un vecteur est un outil mathématique très utilisé en physique. Il vous permet de traiter des collections de nombres (chacun représentant une dimension) d'une manière très efficace. L'ensemble des opérations, des règles et des propriétés permettant de traiter les vecteurs est appelé géométrie vectorielle et, comme pour les nombres, elle inclut la multiplication.

Cependant, les vecteurs sont plus complexes que les nombres, car ils portent en eux beaucoup plus d'informations qui doivent être manipulées plus prudemment. C'est l'une des raisons pour lesquelles, en géométrie vectorielle, il existe deux types différents de multiplications ou d'opérations sur les produits : le produit vectoriel et le produit scalaire. Vous pouvez calculer ce dernier à l'aide de notre calculateur de produit scalaire d'un vecteur 🇺🇸.

La définition, comme c'est souvent le cas en mathématiques, est très technique. Néanmoins, nous allons expliquer ce qu'elle signifie en termes simples (et moins précis) afin que, même si vous n'avez pas de solides connaissances en mathématiques, tout ait un sens pour vous.

Définition du produit vectoriel

Une opération binaire sur deux vecteurs dans un espace à trois dimensions qui est désignée par le symbole ×. Soient deux vecteurs linéairement indépendants, a et b, alors le produit vectoriel, a × b, est un vecteur perpendiculaire à la fois à a et à b et donc normal au plan qui les contient.

Expliquons cela plus simplement. Tout d'abord, la définition parle d'un espace ou plan tridimensionnel comme celui dans lequel nous vivons. C'est en effet l'usage le plus courant du produit vectoriel, mais nous pouvons l'étendre à d'autres dimensions, ce qui dépasse toutefois le cadre de ce texte et de la plupart des diplômes de mathématiques.

La définition nous dit que le produit vectoriel de deux vecteurs quelconques est un troisième vecteur qui est perpendiculaire à ces deux vecteurs (et au plan qui les contient). Cela est possible dans un espace à trois dimensions, car, dans cet espace, il y a trois directions indépendantes. Vous pouvez assimiler ces trois directions à la hauteur, la largeur et la profondeur.

Pour savoir à quoi ressemblera ce nouveau troisième vecteur en termes de norme et de description mathématique, nous pouvons utiliser la formule du produit vectoriel de deux vecteurs. Dans la section suivante, nous vous présenterons la formule mathématique formelle qui vous indique comment effectuer le produit vectoriel de deux vecteurs quelconques. Nous allons également expliquer ce que signifie cette équation et comment l'utiliser de manière simple mais précise.

Avant de présenter la formule du produit vectoriel, nous avons besoin de deux vecteurs que nous appellerons a et b. Ces deux vecteurs ne doivent pas être colinéaires (c'est-à-dire qu'ils ne doivent pas être parallèles) pour des raisons que nous expliquerons plus loin.

Sans plus attendre, voyons la formule :

c = a × b = |a| × |b| × sin θ × n

Cette formule est composée de :

• c – nouveau vecteur résultant du produit vectoriel
• a – un des vecteurs initiaux
• b – le second vecteur initial
• θ – angle entre les deux vecteurs
• n – vecteur unitaire 🇺🇸 perpendiculaire à a et b simultanément

Le facteur de perpendicularité et la fonction sinus présente dans la formule sont de bons indicateurs des interprétations géométriques du produit vectoriel. Nous en parlerons plus en détail dans les sections suivantes.

Vous pouvez également voir pourquoi les deux vecteurs a et b ne doivent pas être parallèles. S'ils étaient parallèles, l'angle entre eux serait nul (θ = 0). Par conséquent, sin θ et c seraient tous deux égaux à zéro, ce qui est un résultat très inintéressant. Il est également intéressant de noter qu'une simple permutation de a et b ne changerait que la direction de c puisque -sin(θ) = sin(-θ).

Nous avons vu la formule mathématique du produit vectoriel, mais vous vous dites peut-être encore : c'est bien beau, mais comment puis-je calculer réellement le nouveau vecteur ? Et c'est une excellente question ! La solution la plus rapide et la plus simple consiste à utiliser notre calculateur de produit vectoriel, mais si vous avez lu jusqu'ici, vous recherchez probablement non seulement des résultats, mais aussi des connaissances.

Nous pouvons diviser le processus en trois étapes différentes : le calcul de la norme d'un vecteur, le calcul de l'angle entre deux vecteurs et le calcul du vecteur unitaire perpendiculaire. En utilisant une simple multiplication, vous obtiendrez le vecteur souhaité en rassemblant ces trois résultats intermédiaires.

Le calcul des angles entre les vecteurs peut s'avérer très compliqué dans l'espace 3D. Alors, nous allons plutôt explorer une manière plus directe et pratique de calculer le produit vectoriel en utilisant une formule de produit vectoriel différente.

Cette nouvelle formule utilise la décomposition d'un vecteur à 3 dimensions en ses trois composantes. Cette technique est une façon très courante de décrire et d'opérer avec des vecteurs dans lesquels chaque composante représente une direction dans l'espace et le nombre qui l'accompagne représente la longueur du vecteur dans la direction spécifique. Canoniquement, les trois dimensions de l'espace 3D avec lequel nous travaillons sont appelées x, y et z et sont représentées par les vecteurs unitaires i, j et k, respectivement.

En suivant cette nomenclature, nous pouvons représenter chaque vecteur par une somme de ces trois vecteurs unitaires. Les vecteurs sont généralement omis par souci de concision, mais ils sont tout de même implicites et ont une grande influence sur le résultat du produit vectoriel. Ainsi, un vecteur v peut être exprimé comme suit : v = (3i + 4j + 1k) ou, en bref : v = (3, 4, 1) où la position des nombres est importante. En utilisant cette notation, nous pouvons maintenant comprendre comment calculer le produit vectoriel de deux vecteurs.

Nous appellerons nos deux vecteurs : v = (v₁, v₂, v₃) et w = (w₁, w₂, w₃). Pour ces deux vecteurs, la formule se présente comme suit :

v × w = (v₂w₃ - v₃w₂, v₃w₁ - v₁w₃, v₁w₂ - v₂w₁)

Ce résultat peut ressembler à une collection aléatoire d'opérateurs entre les composantes de chaque vecteur, mais rien n'est plus loin de la réalité. Pour ceux d'entre vous qui se demandent d'où vient tout cela, nous vous encourageons à le découvrir par vous-même. Tout ce que vous avez à faire est de commencer avec les deux vecteurs exprimés comme suit : v = v₁i + v₂j + v₃k et w = w₁i + w₂j + w₃k et de multiplier chaque composante d'un vecteur avec toutes les composantes de l'autre.

Comme petit indice, nous pouvons vous dire que lorsque l'on fait le produit vectoriel de vecteurs multipliés par des nombres, le résultat est le produit standard des nombres multiplié par le produit vectoriel. Il vous sera également utile de vous rappeler que le produit vectoriel de vecteurs parallèles (et donc d'un vecteur avec lui-même) est toujours égal à 0.

Après tout ce dont nous avons parlé, il est temps d'apprendre comment utiliser notre calculateur de produit vectoriel pour gagner du temps et obtenir des résultats pour deux vecteurs quelconques dans un espace à trois dimensions. Comme vous pouvez le voir, les variables sont divisées en trois sections, une pour chaque vecteur impliqué dans un calcul de produit vectoriel. De ces trois vecteurs, c est probablement celui qui vous sera le plus prudent puisqu'il s'agit du résultat du produit vectoriel. Chaque vecteur a trois composantes, comme mentionné précédemment : x, y, et z, se référant à chacune des trois dimensions : profondeur, largeur, et hauteur.

Maintenant que nous avons compris ce que fait chacune des composantes et donc chacun des champs de ce calculateur de produit vectoriel, voyons ensemble un exemple. Nous utiliserons les vecteurs a = (2, 3, 7) et b = (1, 2, 4).

1. La première étape consiste à saisir les composantes du vecteur a. C'est-à-dire : x = 2, y = 3 et z = 7.

2. Ensuite, vous devez saisir les composantes du vecteur b. À savoir : x = 1, y = 2 et z = 4.

3. Maintenant, le calculateur de produit vectoriel traite l'information ; il applique la formule que nous avons vue précédemment et…

4. Voilà ! Vous venez de calculer votre vecteur :
   c = a × b = (-2, -1, 1)

5. Répétez l'opération jusqu'à ce que vous ayez calculé tous les produits vectoriels dont vous aviez besoin.

6. Partagez avec vos amis l'expérience renversante de calculer un produit vectoriel.

Vous pouvez calculer le produit vectoriel de tous les vecteurs que vous voulez sans même avoir à y penser. Toutefois, nous vous recommandons vivement d'utiliser les propriétés que nous avons mentionnées ci-dessus pour les opérations complexes afin de vous faire gagner du temps et de vous épargner des tracas. Par exemple, si l'un des vecteurs est simplement un multiple de l'autre, vous n'avez même pas besoin d'utiliser notre calculateur de produit vectoriel ; vous pouvez prédire que le résultat sera zéro puisque ces deux vecteurs sont colinéaires.

Nous avons exploré les aspects mathématiques les plus importants du produit vectoriel de deux vecteurs dans l'espace 3D. Il est donc temps d'aborder quelques faits et utilisations intéressants de cette opération vectorielle. Pour commencer, nous allons parler du cousin du produit vectoriel : le produit scalaire.

Bien que similaires au premier coup d'œil, ces deux opérations sont différents concepts en géométrie. En outre, il est sans doute plus facile de calculer le produit scalaire que le produit vectoriel ; néanmoins, nous avons également créé un calculateur qui vous aide à calculer le produit scalaire de deux vecteurs.

Regardons de plus près la formule du produit scalaire :

v = a ⋅ b = |a| × |b| × cos θ

Les seules différences entre le produit vectoriel et le produit scalaire sont la fonction trigonométrique utilisée dans la formule et le fait que le résultat est un nombre (scalaire, d'où le nom) plutôt qu'un vecteur.

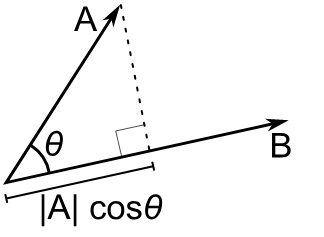
Ces différences mineures pourraient vous faire croire que les deux opérateurs sont très similaires, mais ils sont de nature très différente. Pour commencer, le produit vectoriel est une opération qui prend deux vecteurs et renvoie un autre vecteur perpendiculaire aux deux, alors que le produit scalaire donne un nombre sans direction. Le produit scalaire est plus facile à générer pour des dimensions supérieures ou inférieures, tandis que le produit vectoriel n'existe même pas en 2D. Leur interprétation en termes géométriques est également très différente puisque vous pouvez considérer le produit scalaire comme la longueur de la projection de l'un des vecteurs sur l'autre.

Toutes ces différences en font des opérations très distinctes sur le plan conceptuel. Par conséquent, ces deux opérations ne sont pas interchangeables ou traduisibles. Comme nous le verrons dans les sections suivantes, ces deux opérations jouent un rôle déterminant à la fois en mathématiques et en physique.

La plupart d'entre nous ne s'intéressent pas seulement aux propriétés et utilisations purement mathématiques du produit vectoriel, mais aussi à son application pratique dans la vie réelle. Et quel meilleur moyen d'utiliser les concepts mathématiques de manière utile que la physique ? Le produit vectoriel n'est pas une exception ; c'est une opération très utile en physique. Nous pourrions nous plonger dans la théorie quantique des champs, où le produit scalaire et le produit vectoriel sont tous deux largement utilisés.

Cependant, nous resterons dans le domaine des théories tangibles et mathématiquement parfaites et nous examinerons des exemples auxquels nous pouvons tous nous identifier.

L'électromagnétisme est le premier domaine que nous aborderons et dans lequel les propriétés du produit vectoriel sont largement utilisées. Dans la nature, les champs électriques et magnétiques sont généralement perpendiculaires l'un à l'autre, ce qui correspond parfaitement à la façon dont le produit vectoriel de deux vecteurs est exprimé. Le calcul des forces magnétiques sur un fil porteur de courant ou le calcul du moment magnétique d'un système nécessitent l'utilisation du produit vectoriel.

Un autre exemple incontournable est l'effet Hall, très important en physique des solides. Vous pouvez en apprendre davantage à ce sujet en consultant le calculateur de coefficient de Hall 🇺🇸.

Les applications les plus courantes du produit vectoriel comprennent l'étude du moment d'inertie (comme dans le calculateur de moment d'inertie 🇺🇸) et la rotation d'objets. Nous pourrions parler sans fin de l'aspect époustouflant de cette partie de la physique. Il est préférable de regarder la vidéo dans laquelle Walter Lewin (l'un des meilleurs professeurs de physique) explique et démontre tout ce qu'il faut savoir sur ce phénomène.

Les vecteurs sont omniprésents en physique ; de la vitesse au poids ou même à l'aire, tout semble être associé à un vecteur. C'est la raison pour laquelle le produit vectoriel est très important dans le monde physique.

L'une des choses les plus effrayantes de la physique est de donner un sens à tout le travail mathématique que l'on doit faire pour calculer à peu près n'importe quoi. Lorsque l'on inclut des vecteurs et plusieurs dimensions, cela peut rapidement devenir fouillis et plus rien ne semble à voir avec la réalité. Pour résoudre ces problèmes, les physiciens ont mis au point quelques astuces pour vous aider à naviguer dans ces eaux boueuses.

La plus connue est probablement la « règle de la main droite », qui facilite le calcul du produit vectoriel. Cette règle vous permet de prédire la direction du vecteur résultant du produit vectoriel en utilisant uniquement votre main.

Il existe deux versions de la règle de la main droite en physique : l'une avec les doigts étendus et la main immobile, et l'autre impliquant le passage d'une main ouverte à un poing fermé.

La première version (la plus courante) consiste à déplier le majeur et l'index, comme le montre l'image ci-dessus. Avec le pouce en l'air, vous devez viser à aligner l'index sur le premier vecteur et le majeur sur le second. Dans cette position, le pouce levé indiquera la direction du vecteur résultant du calcul du produit vectoriel.

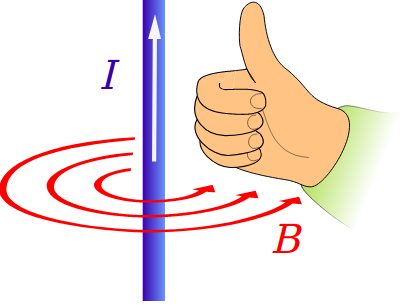
La deuxième méthode est, à notre avis, plus facile à utiliser. Avec une main ouverte, vous alignez les doigts sur le premier vecteur. Ensuite, vous fermez votre main en un poing en direction du deuxième vecteur. Après avoir effectué ces actions, vous obtiendrez une main avec le pouce levé ou le pouce baissé. Comme dans le cas précédent, la direction du pouce indiquera la direction du vecteur résultant de l'opération du produit vectoriel.

Tous ces jeux peuvent sembler enfantins, mais ce sont des astuces puissantes. D'un simple geste de la main, vous pouvez obtenir une perspective non altérée de l'aspect du produit vectoriel. Vous serez peut-être même surpris·e d'apprendre que ces astuces sont continuellement utilisées par les chercheurs chaque fois que leurs travaux impliquent des calculs de produits vectoriels, comme lors de l'utilisation de la formule du calculateur de force électromagnétique 🇺🇸.