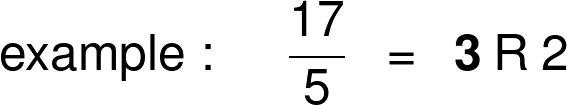Calculateur de quotient

Bienvenue sur le calculateur de quotient d'Omni, où nous nous concentrerons sur les problèmes de division. Nous commencerons par la terminologie et définirons le dividende, le diviseur, le quotient et le reste. Une fois que vous saurez tout ce qu'il faut savoir sur la division en mathématiques, nous vous montrerons des exemples : 4 divisé par 3, 12 divisé par 4, ou 25 divisé par 2. Notre outil est spécialisé dans le calcul des divisions de nombres entiers, bien qu'il affiche également la réponse pour les nombres décimaux.

En mathématiques, la division est l'opération inverse de la multiplication. Pour être précis, si nous calculons :

a × b = c

La division doit prendre le produit ci-dessus et restituer l'un des facteurs :

c / a = b

Cependant, en mathématiques, la division utilise une terminologie différente de celle de la multiplication. Au lieu des facteurs et du produit, nous avons le dividende, le diviseur et le quotient :

dividende / diviseur = quotient

Rappelez-vous que la multiplication (tout comme l'addition) est commutative. En d'autres termes, le a et le b peuvent échanger leurs places dans la première formule de cette section, et le résultat restera le même.

À l'inverse, la division (tout comme la soustraction) n'est pas commutative. Par conséquent, en mathématiques, le dividende est toujours le premier des nombres, tandis que le second est le diviseur (c'est aussi pour cela qu'ils ont des noms différents). Par exemple, c / a est différent de a / c.

Maintenant que vous savez ce que sont le dividende, le diviseur et le quotient, voyons l'opération en elle-même et les deux résultats affichés par le calculateur Omni. En fait, tout se résume à savoir si les fractions sont tolérées ou pas.

Les problèmes de division consistent à déterminer combien de fois une quantité totale peut être divisée en parts égales. Par exemple, supposons que vous achetiez une grande pizza de 8 parts pour une famille de 4. Pour calculer le nombre de parts que chaque personne reçoit, nous utilisons la division :

8 / 4 = 2

Mais que se passerait-il s'il y avait 3 personnes à la place ? Évidemment, tout le monde pourrait encore avoir deux parts, mais il en resterait deux dans la boîte. Maintenant, la question est de savoir si nous voulons les garder pour plus tard ou les couper en plus petits morceaux. Et c'est là que le quotient et le reste interviennent.

Comme indiqué dans la section ci-dessus, le résultat de la division s'appelle le quotient. Cependant, tous les nombres ne sont pas divisibles par un autre (comme 4 divisé par 3 ou 25 divisé par 2). Dans de tels cas, on peut distribuer le dividende en parts égales tant que possible, jusqu'à ce qu'il reste des parts non divisibles. Ce sont ces parts qui constituent le reste.

Dans l'exemple de la pizza ci-dessus, une pizza de 8 parts pour 3 correspond à 2 parts par personne avec un reste de 2. D'autres exemples seraient, disons, 4 divisé par 3, qui donne 1 avec un reste de 1, ou 25 divisé par 2, qui est égal à 12 avec un reste de 1. On peut écrire le résultat d'une telle division en mathématiques en séparant le quotient et le reste par un R majuscule (voir ci-dessous).

• 8 / 3 = 2 R 2

• 4 / 3 = 1 R 1

• 25 / 2 = 12 R 1

Nous pouvons également utiliser cette notation lorsque, dans un problème de mathématiques, le dividende est plus petit que le diviseur :

• 2 / 3 = 0 R 2

• 17 / 20 = 0 R 17

Ou lorsque les nombres sont divisibles entre eux, comme 12 divisé par 4 :

• 12 / 4 = 3 R 0

Cependant, il faut être prudent avec les restes quand il s'agit de nombres négatifs. En règle générale, nous définissons le reste en mathématiques comme un nombre positif plus petit que la valeur absolue du diviseur. Néanmoins, certaines applications (notamment en informatique) autorisent les restes négatifs. Ainsi, si vous utilisez le calculateur pour trouver le quotient de, disons, -4 divisé par 3 ou 25 divisé par -2, vous obtiendrez deux résultats :

(-4) / 3 = -1 R (-1) = -2 R 2

25 / (-2) = -13 R (-1)= -12 R 1

Enfin, mentionnons que nous voulons parfois aborder les problèmes de division sans mentionner le reste. Si nous reprenons l'exemple d'une pizza de 8 parts pour 3 personnes, cela signifierait découper les 2 parts restantes en plus petits morceaux pour la terminer. Mathématiquement parlant, cela se traduit par un quotient fractionnaire.

8 / 3 = 2⅔ ≈ 2,666

En fait, tout le monde reçoit deux parts de pizza complètes et deux tiers d'un autre part. Si nécessaire, assurez-vous de consulter notre convertisseur de fractions en décimales 🇺🇸.

Comme vous pouvez le constater, notre calculateur est pratique pour trouver le quotient, quelle que soit la forme dont vous avez besoin. Un bel outil, n'est-ce pas ? Regardons désormais comment s'en servir.

En haut de notre outil, vous pouvez voir la formule de division que nous utilisons dans notre calculateur de quotient. Par exemple, si vous voulez savoir ce que représente 15 divisé par 6, vous devez :

1. Entrer 15 dans le champ de la variable « Dividende ».
2. Saisir 6 dans le champ de la variable « Diviseur ».
3. Lire le résultat en dessous sous la forme que vous souhaitez.
4. Admirer le résultat et s'en venter auprès de vos amis.

Comme indiqué au point 3 et dans la section ci-dessus, rappelez-vous que le calculateur de quotient donne la réponse sous différentes formes : soit une fraction (un nombre fractionnaire ou un nombre décimal), soit un quotient et un reste. Pour les nombres entiers négatifs, vous pouvez vous attendre à deux variantes du reste, tandis que pour les nombres décimaux, le calculateur de quotient renvoie simplement le résultat de la division sans aucune sortie supplémentaire (il n'y a pas de reste dans ce cas).

Quelle que soit la forme que vous choisissez, nous espérons que notre outil vous apportera ce dont vous avez besoin. N'oubliez pas que le calculateur de quotient n'est qu'un des nombreux outils arithmétiques que nous vous proposons.

Pour diviser deux nombres, disons a par b, vous devez :

1. Prendre le premier chiffre de a.

2. Diviser ce dernier par b.

3. Écrire le quotient de l'étape 2 comme premier chiffre du résultat.

4. Écrire le reste de l'étape 2 en dessous.

5. Écrire le chiffre suivant de a à droite du nombre de l'étape 4.

6. Répéter les étapes 1 à 5 pour les chiffres suivants de a.

7. Le quotient est constitué des chiffres de l'étape 3.

8. Le reste est ce que vous avez après avoir épuisé les chiffres de a.

Pour trouver le quotient de deux nombres, disons a et b, vous devez :

1. Prendre le premier chiffre de a.

2. Diviser ce dernier par b.

3. Écrire le quotient de l'étape 2 comme premier chiffre du résultat.

4. Écrire le reste de l'étape 2 en dessous.

5. Écrire le chiffre suivant de a à droite du nombre de l'étape 4.

6. Répéter les étapes 1 à 5 pour les chiffres suivants de a

7. Le quotient est constitué des chiffres de l'étape 3.

8. Le reste est ce qu'il vous reste après avoir épuisé les chiffres de a.

Oui. Le résultat de la division de deux nombres (le dividende par le diviseur) s'appelle le quotient.

Pour estimer le quotient de deux nombres, disons a et b, vous devez :

1. Prendre le premier chiffre de a.

2. Diviser ce dernier par b.

3. Écrire le quotient de l'étape 2 comme premier chiffre du résultat.

4. Écrire le reste de l'étape 2 en dessous.

5. Écrire le chiffre suivant de a à droite du nombre de l'étape 4.

6. Répéter les étapes 1 à 5 pour les chiffres suivants de a.

7. Mettre la virgule décimale après le résultat que vous avez obtenu jusqu'à présent.

8. Répéter les étapes 1 à 5, mais avec des zéros à l'étape 5.

9. Arrêter lorsque vous avez obtenu une estimation satisfaisante.

Oui. Par définition, un nombre rationnel est un nombre que l'on peut représenter comme un nombre entier divisé par un autre, ce qui est précisément ce que la question mentionne.

Pour trouver le quotient et le reste de deux nombres sans division réelle, disons, de a et b, vous devez :

1. Soustraire b de a.
2. Soustraire b du résultat obtenu à l'étape 1.
3. Répéter l'opération jusqu'à ce que vous ne puissiez plus soustraire b.
4. Le quotient est le nombre de fois que vous avez soustrait b.
5. Le reste est ce qu'il vous reste après l'étape 3.
6. Admirer le quotient et le reste de votre division.