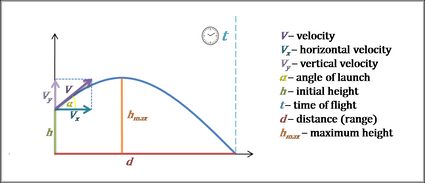
Calculateur de trajectoire parabolique

Notre calculateur de trajectoire parabolique est un outil qui vous aidera à analyser le mouvement parabolique d'un projectile. Il vous permettra de déterminer le temps de vol, mais aussi les composantes du vecteur vitesse, la portée du projectile et la hauteur maximale de la trajectoire. Continuez la lecture pour déterminer toutes ces valeurs et pour connaitre la définition du mouvement parabolique.
Vous êtes plutôt du genre à regarder une vidéo que de lire un pavé ? Si vous avez 90 secondes devant vous, nous avons réalisé une petite animation qui vous expliquera tout sur le sujet :

Imaginez qu'un archer envoie une flèche en l'air. La flèche est propulsée vers le haut et vers l'avant, à un angle par rapport au sol. Plus elle vole loin, plus son ascension est lente. Finalement, elle commence à descendre, se déplaçant maintenant vers le bas, mais toujours vers l'avant jusqu'à toucher à nouveau le sol. Si vous pouviez retracer sa trajectoire, vous obtiendriez une courbe appelée trajectoire parabolique. Ce type de trajectoire est suivi par tout objet après avoir été lancé.

D'ailleurs, nous avons créé le calculateur de vitesse d'une flèche qui analyse le mouvement des flèches. Jetez un coup d'œil !

Une seule force agit sur un objet en mouvement parabolique : la force de gravité. La résistance de l'air est toujours omise. Si vous vouliez dessiner un diagramme des forces agissant sur un tel objet, vous n'auriez qu'à tracer un vecteur dirigé vers le bas que vous nommeriez « gravité ». Si d'autres forces agissaient sur le corps, il ne s'agirait plus d'un mouvement parabolique, d'après la définition de celui-ci.

Le mouvement parabolique est assez logique. Supposons que la vitesse initiale du projectile est $V$, l'angle de lancement est $\alpha$, et la hauteur initiale est $h$. Notre calculateur de trajectoire parabolique trouvera tous les paramètres manquants. Voilà toutes les étapes suiviez par le calculateur :

1. Calculez les composantes du vecteur vitesse.

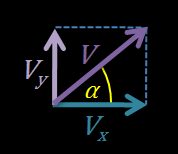
• La composante horizontale du vecteur vitesse $V_\mathrm x$ est égale à $V \cos\alpha$.
• La composante verticale du vecteur vitesse $V_\mathrm y$ est égale à $V \sin\alpha$.

Les trois vecteurs, $V$, $V_\mathrm x$ et $V_\mathrm y$, forment un triangle droit.

Si la composante verticale du vecteur vitesse est égale à 0, le mouvement est horizontal. En revanche, si α = 90°, il s'agit d'une chute libre. Nous avons abordé ces deux questions, respectivement, dans le calculateur de trajectoire d'un projectile horizontal 🇺🇸 et le calculateur de chute libre.

2. Notez les équations du mouvement.

Distance 

• La distance horizontale parcourue est égale à $x = V_\mathrm x t$ (où $t$ est le temps).
• La distance verticale par rapport au sol est égale à $y = h + V_\mathrm{y0} t - g t^2 / 2$ (où $g$ est l'accélération gravitationnelle, et $V_\mathrm{y0}$, la vitesse verticale initiale).

Vitesse 

• La vitesse horizontale est égale à $V_\mathrm x$.
• La vitesse verticale est égale à $V_\mathrm y = V_\mathrm{y0} - g t$.

Accélération 

• L'accélération horizontale est égale à 0.
• L'accélération verticale est égale à $-g$ (car seule la gravité agit sur l'objet).

3. Calculez le temps de vol.

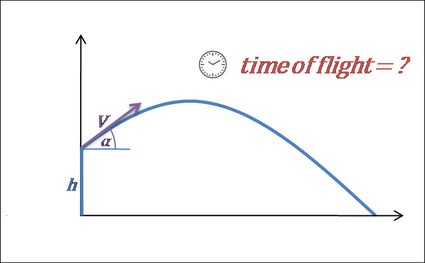
• Le vol se termine dès que le projectile touche le sol, c'est-à-dire lorsque sa distance verticale par rapport au sol atteint 0. Quand la hauteur initiale est égale à 0, la formule peut s'écrire comme suit : $V_\mathrm{y0} t - g t^2 / 2 = 0$. À partir de cette équation, nous pouvons dériver la formule du temps de vol  :

• Cependant, si le projectile est lancé d'une certaine hauteur, la formule n'est pas aussi facilement dérivable. En effet, il faut résoudre une équation quadratique, $h + V_\mathrm{y0} t - g t^2 / 2 = 0$, jusqu'à obtenir :

4. Trouvez la portée du projectile.

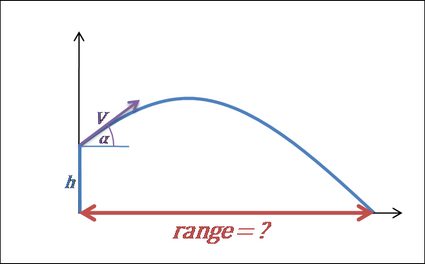
• La portée est la distance horizontale parcourue par l'objet lors du vol. Similairement à la formule du temps de vol, si l'objet est lancé depuis le sol (donc, avec une hauteur initiale égale à 0), la formule est : $R = V_\mathrm x t = V_\mathrm x \times 2 \times V_\mathrm{y0} / g$, ou bien $R = V^2_0 \sin(2\alpha) / g$.

• Si la hauteur initiale est supérieure à 0, cela devient plus compliqué : il faut substituer $t$ par l'équation du temps de vol de l'étape précédente.

• La portée est particulièrement importante en balistique. Nous en avons parlé plus en détail dans notre calculateur de coefficient balistique 🇺🇸.

5. Calculez la hauteur maximale.

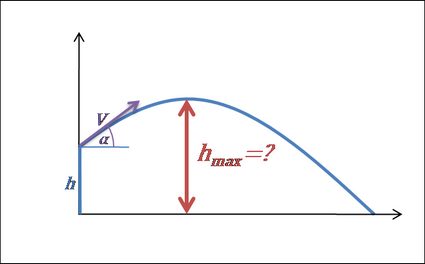
• Dès que le projectile atteint sa hauteur maximale, il cesse de monter et commence sa descente. Ainsi, la composante verticale du vecteur vitesse devient négative, après avoir atteint 0 pendant un court instant à $t(V_\mathrm y=0)$.
• Si $V_\mathrm {y0} - g t(V_\mathrm y=0) = 0$, nous pouvons reformuler cette équation : $t(V_\mathrm y=0) = V_\mathrm{y0} / g$
• Il ne nous reste plus qu'à trouver la distance verticale par rapport au sol à ce moment-là :

• Heureusement, si le projectile a une certaine hauteur initiale $h$ supérieure à 0, il suffit d'ajouter cette valeur dans la formule finale :

Ouf, beaucoup de calculs ! Voilà une petite récapitulation pour bien comprendre quelles sont les équations fondamentales du mouvement parabolique :

1. Lancement du projectile depuis le sol (hauteur initiale h = 0)

• composante horizontale du vecteur vitesse – $V_\mathrm x = V_0 \cos \alpha$
• composante verticale du vecteur vitesse – $V_\mathrm y = V_0 \sin \alpha - gt$
• temps de vol – $t = 2 V_\mathrm{y0} / g$
• portée du projectile – $R = 2 V_\mathrm x V_\mathrm{y0} / g$
• hauteur maximale – $h_\mathrm{max} = V^2_\mathrm{y0} / (2 g)$

2. Lancement du projectile à partir d'une certaine hauteur (hauteur initiale h > 0)

• composante horizontale du vecteur vitesse – $V_\mathrm x = V_0 \cos \alpha$
• composante verticale du vecteur vitesse – $V_\mathrm y = V _0 \sin \alpha - gt$
• temps de vol – $t = \left[V_\mathrm{y0} + \sqrt{V^2_\mathrm{y0} + 2 g h}\right] / g$
• portée du projectile – $R = V_\mathrm x \left[V_\mathrm{y0} + \sqrt{V^2_\mathrm{y0} + 2 g h}\right] / g$
• hauteur maximale – $h_\mathrm{max} = h + V^2_ \mathrm{y0} / (2 g)$

Notre calculateur de trajectoire parabolique vous permettra d'économiser du temps. Il fonctionne aussi bien « à l'envers » : saisissez le temps de vol, la distance et la hauteur initiale, par exemple, et le calculateur fera tous les calculs pour vous !

N'oubliez pas de consulter le calculateur de parabole pour en savoir plus sur ce type de courbe d'un point de vue mathématique.