Calculateur de test Z

Ce calculateur de test Z vous aide à effectuer un test Z à un échantillon sur la moyenne de la population. Il existe deux formes de ce test (le test Z bilatéral et le test Z unilatéral) qui peuvent être utilisées en fonction de vos objectifs. Vous pouvez également choisir si le calculateur doit déterminer la valeur p du test Z ou si vous préférez utiliser l'approche de la valeur critique !

Poursuivez votre lecture pour en savoir plus sur le test Z en statistique et, en particulier, pour savoir quand utiliser les tests Z, quelle est la formule du test Z et s'il convient d'utiliser le test Z plutôt que le test de Student. En prime, nous vous proposons quelques exemples pour apprendre à effectuer des tests Z pas à pas !

Vous pouvez également consulter notre calculateur de statistiques du test de Student, qui vous permettra d'apprendre le concept d'une autre statistique essentielle. Si vous êtes par ailleurs intéressé·e par le test F, consultez notre calculateur de statistiques du test F 🇺🇸.

Le test Z à un échantillon est l'un des tests de position les plus populaires. L'hypothèse nulle est que la valeur moyenne de la population est égale à un nombre donné, $\mu_0$ :

Nous effectuons un test Z bilatéral pour tester si la moyenne de la population n'est pas $\mu_0$ :

Nous effectuons un test Z unilatéral pour tester si la moyenne de la population est inférieure ou supérieure à $\mu_0$ :

Examinons maintenant les hypothèses d'un test Z à un échantillon.

Vous pouvez utiliser un test Z si votre échantillon est constitué de points de données indépendants et :

• les données sont normalement distribuées, et vous connaissez la variance de la population ; ou

• l'échantillon est grand et les données suivent une distribution dont la moyenne et la variance sont finies. Vous n'avez pas besoin de connaître la variance de la population.

La raison pour laquelle ces deux possibilités existent est que nous voulons que les statistiques de test suivent la loi normale centrée réduite $\mathrm N(0, 1)$. Dans le premier cas, il s'agit d'une loi normale centrée réduite exacte, tandis que dans le second, elle l'est approximativement, grâce au théorème de la limite centrale.

Une question demeure : quand mon échantillon est-il considéré comme grand ? Il n'y a pas de critère universel. En général, plus vous avez de points de données, mieux l'approximation fonctionne. Les manuels de statistique recommandent de disposer d'au moins 50 points de données, tandis que 30 est considéré comme le strict minimum.

Soit $x_1, ..., x_n$ un échantillon indépendant suivant la loi normale $\mathrm N(\mu, \sigma^2)$, c'est-à-dire avec une moyenne égale à $\mu$, et une variance égale à $\sigma ^2$.

Nous prenons l'hypothèse nulle :

$\mathrm H_0 \!:\!\! \mu = \mu_0$

Nous définissons la statistique de test, Z, comme suit :

où :

• $\bar x$ – la moyenne de l'échantillon, soit $\bar x = (x_1 + ... + x_n) / n$

• $\mu_0$ – la moyenne établie dans $\mathrm H_0$

• $n$ – la taille d'échantillon

• $\sigma$ – l'écart type de la population

Dans ce qui suit, $Z$ majuscule représente la statistique du test (traitée comme une variable aléatoire), tandis que $z$ minuscule désigne une valeur réelle de $Z$, calculée pour un échantillon donné tiré de N(μ,σ²).

Si $\mathrm H_0$ est valable, la somme $S_n = x_1 + ... + x_n$ suit la distribution normale, avec une moyenne $n \mu_0$ et une variance $n^2 \sigma$. Comme $Z$ est la normalisation (score Z) de $S_n/n$, nous pouvons conclure que la statistique du test $Z$ suit la loi normale centrée réduite $\mathrm N(0, 1)$, à condition que $\mathrm H_0$ soit vrai. D'ailleurs, nous avons le calculateur de score Z si vous voulez vous concentrer sur ce seul score.

Si nos données ne suivent pas une loi normale, ou si l'écart type de la population est inconnu (et donc dans la formule pour $Z$ nous remplaçons l'écart type de la population $\sigma$ par l'écart type de l'échantillon), alors la statistique du test $Z$ ne suit pas nécessairement une loi normale. Cependant, si l'échantillon est suffisamment grand, le théorème de la limite centrale garantit que $Z$ suit approximativement $\mathrm N(0, 1)$.

Dans les sections suivantes, nous vous expliquerons comment utiliser la valeur de la statistique de test, $z$, pour prendre une décision, et s'il faut ou non rejeter l'hypothèse nulle. Deux approches peuvent être utilisées pour parvenir à cette décision : l'approche de la valeur p et l'approche de la valeur critique ; et nous expliquons les deux approches ! Laquelle devriez-vous utiliser ? Dans le passé, l'approche de la valeur critique était plus populaire parce qu'il était difficile de calculer la valeur p à partir d'un test Z. Cependant, grâce aux ordinateurs modernes, nous pouvons le faire assez facilement, et avec une bonne précision. En général, il est fortement conseillé de donner la valeur p de vos tests !

Formellement, la valeur p est le plus petit seuil de signification auquel l'hypothèse nulle peut être rejetée. Plus intuitivement, la valeur p répond aux questions suivantes.
À condition que l'on vive dans un monde où l'hypothèse nulle se vérifie, quelle est la probabilité que la valeur de la statistique du test soit au moins aussi extrême que la valeur $z$ que l'on a obtenue pour notre échantillon ? Par conséquent, une petite valeur p signifie que votre résultat est très improbable sous l'hypothèse nulle, et qu'il y a donc une forte probabilité que l'hypothèse nulle soit rejetée (plus la valeur p est petite, plus la probabilité que l'hypothèse soit rejetée est forte).

Pour trouver la valeur p, vous devez calculer la probabilité que la statistique du test, $Z$, soit au moins aussi extrême que la valeur observée, $z$, si l'hypothèse nulle est vraie (la probabilité d'un événement calculée en supposant que $\mathrm H_0$ est vraie sera notée $\small \mathrm{P}(\text{évènement} | \mathrm{H_0})$.) C'est l'hypothèse alternative qui détermine ce que signifie plus extrême :

1. Test Z bilatéral : les valeurs extrêmes sont celles dont la valeur absolue dépasse $|z|$, c'est-à-dire celles qui sont inférieures à $-|z|$ ou supérieures à $|z|$. Par conséquent, nous avons :

La symétrie de la loi normale donne :

2. Test Z unilatéral à gauche : les valeurs extrêmes sont celles qui sont inférieures à $z$, ce qui nous donne :

3. Test Z unilatéral à droite : les valeurs extrêmes sont celles qui sont supérieures à $z$, nous avons donc :

Pour calculer ces probabilités, nous pouvons utiliser la fonction de répartition (angl. cumulative distribution function, cdf) de $\mathrm N(0, 1)$, qui, pour un nombre réel, $x$, est définie comme suit :

En outre, les valeurs p peuvent être représentées comme l'aire sous la fonction de densité (angl. probability density function, pdf) de $\mathrm N(0, 1)$, en raison de :

Avec tout ce que vous avez appris dans la section précédente, vous êtes prêt·e à vous familiariser avec les tests Z.

1. Test Z bilatéral :

Du fait que $\Phi(-z) = 1 - \Phi(z)$, on en déduit que :

La valeur p est l'aire sous la fonction de densité (pdf) à la fois à gauche de $-|z|$, et à droite de $|z|$:

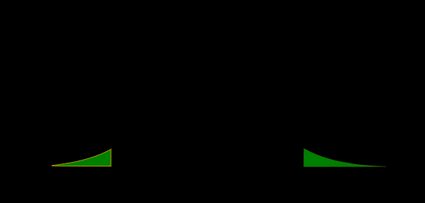
2. Test Z unilatéral à gauche :

La valeur p est l'aire sous la courbe de la fonction de densité à gauche de notre $z$ :

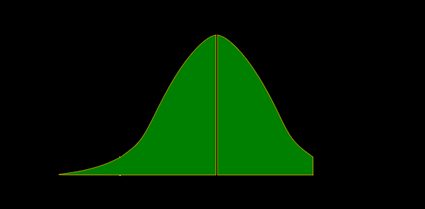
3. Test Z unilatéral à droite :

La valeur p est l'aire sous la courbe de la fonction de densité à droite de $z$ :

La décision de rejeter ou non l'hypothèse nulle peut maintenant être prise à n'importe quel seuil de signification, $\alpha$, que vous souhaitez !

• Si la valeur p est inférieure ou égale à $\alpha$, l'hypothèse nulle est rejetée à ce seuil de signification.

• Si la valeur p est supérieure à $\alpha$, il n'y a pas suffisamment de preuves pour rejeter l'hypothèse nulle à ce seuil de signification.

L'approche des valeurs critiques consiste à comparer la valeur de la statistique de test obtenue pour notre échantillon, $z$, aux valeurs dites critiques. Ces valeurs constituent les limites des régions où il est très improbable que la statistique du test se trouve. Ces régions sont souvent appelées régions critiques ou régions de rejet. La décision de rejeter ou non l'hypothèse nulle repose alors sur l'appartenance ou non de notre $z$ à la région critique.

Les régions critiques dépendent du seuil de signification, $\alpha$, du test et de l'hypothèse alternative. Le choix de $\alpha$ est arbitraire ; dans la pratique, les valeurs de 0,1, 0,05 ou 0,01 sont le plus souvent utilisées pour $\alpha$.

Une fois que nous nous sommes mis d'accord sur la valeur de $\alpha$, nous pouvons facilement déterminer les régions critiques du test Z :

1. Test Z bilatéral :

2. Test Z unilatéral à gauche :

3. Test Z unilatéral à droite :

Pour décider du sort de $\mathrm H_0$, vérifiez si votre $z$ se trouve ou non dans la région critique.

• Si oui, rejetez $\mathrm H_0$ et acceptez $\mathrm H_1$.

• Si non, il n'y a pas suffisamment de preuves pour rejeter $\mathrm H_0$.

Comme vous le voyez, les formules pour les valeurs critiques des tests Z impliquent l'inverse, $\Phi^{-1}$, de la fonction de répartition (cdf) de $\mathrm N(0, 1)$.

Notre calculateur vous simplifie la vie !

1. Choisissez l'hypothèse alternative : bilatérale ou unilatérale à gauche/à droite.

2. Dans notre calculateur de test Z, vous pouvez décider d'utiliser la valeur p ou l'approche des régions critiques. Dans ce dernier cas, définissez le seuil de signification, $\alpha$.

3. Saisissez la valeur de la statistique de test, $z$. Si vous ne la connaissez pas, vous pouvez entrer certaines données qui nous permettront de calculer votre $z$.

   • Moyenne de l'échantillon $\bar x$ (si vous disposez de données brutes, consultez le calculateur de moyenne arithmétique pour déterminer la moyenne).
   • Moyenne testée $\mu_0$.
   • Taille de l'échantillon $n$.
   • L'écart type de la population $\sigma$ (ou l'écart type de l'échantillon si votre échantillon est grand).

4. Les résultats apparaissent immédiatement au bas du calculateur.

Si vous souhaitez trouver $z$ sur la base de la valeur p, n'oubliez pas que dans le cas de tests bilatéraux, il existe deux valeurs possibles de $z$ : une positive et une négative, et qu'il s'agit de nombres opposés. Dans ce cas, le calculateur de test Z renvoie la valeur positive. Pour trouver l'autre valeur possible de $z$ pour une valeur p donnée, il suffit de prendre le nombre opposé à la valeur de $z$ affichée par le calculateur.

Pour s'assurer que vous avez bien compris l'essence du test Z, passons en revue quelques exemples :

1. Une machine pour remplir des bouteilles suit une loi normale. Son écart type, tel que déclaré par le fabricant, est égal à 30 mL. Un vendeur de jus de fruits affirme que le volume versé dans chaque bouteille est, en moyenne, d'un litre, soit 1 000 mL, mais nous soupçonnons qu'en fait le volume moyen est plus petit que cela…

   Formellement, les hypothèses que nous posons sont les suivantes :

   • $\mathrm H_0 \! : \mu = 1\,000 \text{ mL}$

   • $\mathrm H_1 \! : \mu \lt 1\,000 \text{ mL}$

   Nous sommes allés dans un magasin et avons acheté un échantillon de 9 bouteilles. Après avoir mesuré prudemment le volume de jus de chaque bouteille, nous avons obtenu l'échantillon suivant (en millilitres).

   $\footnotesize 1\,020, 970, 1\,000, 980, 1\,010, 930, 950, 980, 980$

   • Taille de l'échantillon : $n = 9$.

   • Moyenne de l'échantillon : $\bar x = 980 \ \mathrm{mL}$.

   • Écart type de la population : $\sigma = 30 \ \mathrm{mL}$.

   • Ainsi, nous obtenons :

• Par conséquent, $\text{valeur p} = \Phi(-2) \approx 0,\!022\,8$.

  Comme $0,\!022\,8 \lt 0,\!05$, nous concluons que nos soupçons ne sont pas infondés ; au seuil de signification le plus courant, 0,05, nous rejetterions l'affirmation du producteur, $\mathrm H_0$, et accepterions l'hypothèse alternative, $\mathrm H_1$.

2. Nous avons lancé une pièce de monnaie 50 fois. Nous avons obtenu 20 fois pile et 30 fois face. Les preuves sont-elles suffisantes pour affirmer que la pièce est pipée ?

   Il est clair que nos données suivent une loi de Bernoulli, avec une probabilité de succès $p$ et une variance $\sigma^2 = p (1-p)$. Cependant, l'échantillon étant grand, nous pouvons effectuer un test Z en toute sécurité. Nous adoptons la convention selon laquelle le fait d'obtenir pile est un succès.

   Énonçons l'hypothèse nulle et l'hypothèse alternative.

   • $\mathrm H_0 \! : p = 0,\!5$ (la pièce est équilibrée: la probabilité d'obtenir pile est de $0,\!5$).

   • $\mathrm H_1 \! : p \ne 0,\!5$ (la pièce est pipée : la probabilité d'obtenir pile diffère de $0,\!5$).

   Dans notre échantillon, nous avons 20 succès (notés par des 1) et 30 échecs (notés par des 0).

   • Taille de l'échantillon $n = 50$.

   • Moyenne de l'échantillon $\bar x = 20/50 = 0,\!4$.

   • L'écart type de la population est donné par $\sigma = \sqrt{0,\!5 \times 0,\!5}$ (car $0,\!5$ est la proportion $p$ supposée dans $\mathrm H_0$). Par conséquent, $\sigma = 0,\!5$.

• Nous avons :

• Et, nous obtenons :

Parce que $0,\!1573 \gt 0,\!1$ nous n'avons pas assez de preuves pour rejeter l'affirmation selon laquelle la pièce est juste, même à un seuil de signification aussi élevé que $0,\!1$. Dans ce cas, vous pouvez lancer votre pièce sans crainte ou utiliser le calculateur de pile ou face pour connaître vos chances d'obtenir, par exemple, 10 face d'affilée (ces chances sont extrêmement faibles !).