Calcolatore per la Legge di Snell

Quando la luce passa da un mezzo all'altro, si piega o si rifrange. Il calcolatore per la legge di Snell ti permette di approfondire questo argomento e di comprendere i principi della rifrazione. Continua a leggere per scoprire tutto sulla legge di Snell sulla rifrazione, e per imparare quale equazione permette di calcolare l'angolo di rifrazione. L'ultima parte di questo articolo è dedicata alla formula e alla definizione dell'angolo critico.

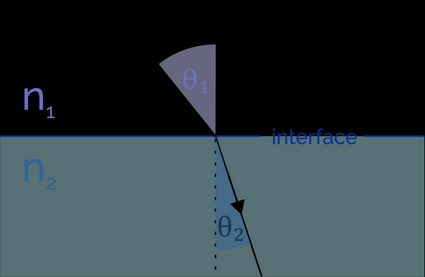
La legge di Snell descrive come funziona esattamente la rifrazione. Quando un raggio di luce entra in un mezzo diverso, la sua velocità e la sua lunghezza d'onda cambiano. Il raggio si piega verso la normale alla superficie di separazione tra due mezzi (quando la sua velocità diminuisce) o si allontana dalla normale (quando la sua velocità aumenta). L'angolo di rifrazione dipende dagli indici di rifrazione dei due mezzi:

dove:

• $n_1$ — Indice di rifrazione del primo mezzo (dal quale viaggia il raggio);
• $n_2$ — Indice di rifrazione del secondo mezzo (verso il quale viaggia il raggio);
• $\theta_1$ — Angolo di incidenza, ovvero l'angolo tra la normale (perpendicolare) alla superficie di separazione tra due mezzi e il raggio in arrivo;
• $\theta_2$ — Angolo di rifrazione, ovvero l'angolo tra la normale alla superficie di separazione e il raggio che viaggia attraverso il secondo mezzo.

Puoi trovare alcuni valori di $n_1$ e $n_2$ per i mezzi più comuni nel calcolatore dell'indice di rifrazione.

In generale, la legge di Snell sulla rifrazione è valida solo per i mezzi isotropi. In quelli anisotropi, come i cristalli, il raggio può dividersi in due.

Supponiamo di voler trovare l'angolo di rifrazione di un raggio di luce che passa dall'aria al vetro. L'angolo di incidenza è di 30°.

1. Trova l'indice di rifrazione dell'aria. È uguale a $1,\!00029\:3$;

2. Trova l'indice di rifrazione del vetro. Supponiamo che sia uguale a $1,\!50$;

3. Trasforma l'equazione in modo che l'incognita (angolo di rifrazione) sia sul lato sinistro: $\sin(\theta_2) = \frac{n_1 \sin(\theta_1)}{n_2}$;

4. Esegui i calcoli: $\sin(\theta_2) = \frac{1,00029\:3 \sin(30\degree)}{1,50} = 0,\!333$;

5. Trova l'arcsin di questo valore: $\theta_2 = \arcsin(0,\!333) = 19,\!48 \degree$; e

6. Puoi anche risparmiare tempo e utilizzare il calcolatore per la legge di Snell.

A volte, applicando la legge di Snell sulla rifrazione, il valore $\sin(\theta_2)$ è maggiore di 1. Questo è ovviamente impossibile. Se ottieni un valore maggiore di 1, significa che tutta la luce viene riflessa dalla superficie di separazione (questo fenomeno è noto come riflessione interna totale). Il nostro calcolatore per la legge di Snell ti avvertirà se qualcosa va storto.

L'angolo di incidenza più alto, per il quale la luce non viene riflessa, è chiamato angolo critico. Il raggio rifratto viaggia lungo la superficie di separazione tra i due mezzi. Ciò significa che l'angolo di rifrazione è uguale a 90°. Quindi, puoi trovare l'angolo critico utilizzando la seguente equazione:

Dopo la semplificazione, $n_1 \sin(\theta_1) = n_2 \times 1$.

Risolvendo l'angolo di incidenza, $\theta_1 = \arcsin(\frac{n_2}{n_1})$.