Calcolatore per l'Angolo del Triangolo

Il calcolatore per l'angolo del triangolo è una garanzia se vuoi sapere come trovare l'angolo di un triangolo. Che tu abbia tre lati di un triangolo, due lati e un angolo o solo due angoli, questo strumento è la soluzione ai tuoi problemi di geometria. Di seguito troverai anche la spiegazione delle leggi fondamentali sugli angoli dei triangoli — teorema della somma degli angoli del triangolo, teorema dell'angolo esterno del triangolo e teorema della bisettrice dell'angolo. Continua a leggere per capire come funziona il calcolatore e provalo — trovare gli angoli mancanti nei triangoli non è mai stato così facile!

Ci sono diversi modi per trovare gli angoli di un triangolo, a seconda dei dati che si hanno a disposizione:

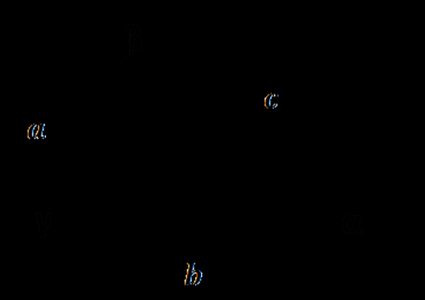
1. Dati tre lati di un triangolo

Usa le formule trasformate dalla legge dei coseni:

Quindi:

Per il secondo angolo abbiamo:

Quindi:

E alla fine, per il terzo angolo:

Quindi:

2. Dati due lati e un angolo

Se l'angolo è compreso tra i lati dati, puoi usare direttamente la legge dei coseni per trovare il terzo lato sconosciuto e poi usare le formule precedenti per trovare gli angoli mancanti, ad esempio dati a, b, γ:

• Calcola $c = \sqrt{a^2 + b^2 - 2ab \times \cos(\gamma)}$;
• Sostituisci $c$ in $\alpha = \mathrm{arccos}\left((b^2 + c^2- a^2)/(2bc)\right)$;
• Quindi trova $\beta$ dal teorema della somma degli angoli del triangolo: $\beta = 180\degree- \alpha - \gamma$.

Se l'angolo non è compreso tra i lati indicati, puoi usare la legge dei seni. Ad esempio, supponiamo di conoscere $a$, $b$ e $\alpha$:

Quindi:

• Come sai, la somma degli angoli di un triangolo è uguale a $180\degree$. Da questo teorema possiamo trovare l'angolo mancante: $\gamma = 180\degree- \alpha - \beta$.

3. Dati due angoli

Questa è l'opzione più semplice. Basta utilizzare il teorema della somma degli angoli del triangolo per trovare l'angolo mancante:

• $\alpha = 180\degree- \beta - \gamma$;
• $\beta= 180\degree- \alpha - \gamma$; e
• $\gamma = 180\degree- \alpha- \beta$.

In tutti e tre i casi, puoi usare il nostro calcolatore per l'angolo del triangolo: non ti deluderà.

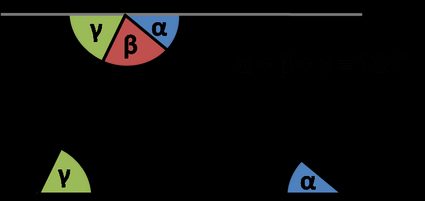
Il teorema afferma che gli angoli interni di un triangolo si sommano a $180\degree$:

Come facciamo a saperlo? Guarda l'immagine — gli angoli indicati con le stesse lettere greche sono congruenti perché sono angoli interni alterni. La somma dei tre angoli $\alpha$ $\beta$ , $\gamma$ è uguale a $180\degree$, poiché formano una linea retta. Ma questi sono tre angoli interni di un triangolo! Ecco perché $\alpha + \beta+ \gamma = 180\degree$.

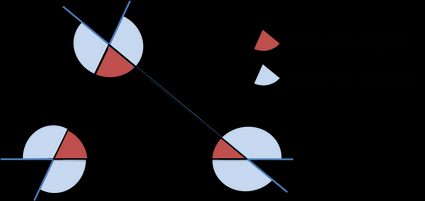
L'angolo esterno di un triangolo è uguale alla somma degli angoli interni opposti.

• Ogni triangolo ha sei angoli esterni (due per ogni vertice sono di misura uguale);
• Gli angoli esterni, presi uno per ogni vertice, si sommano sempre a $360\degree$; e
• Un angolo esterno è supplementare all'angolo interno del triangolo adiacente.

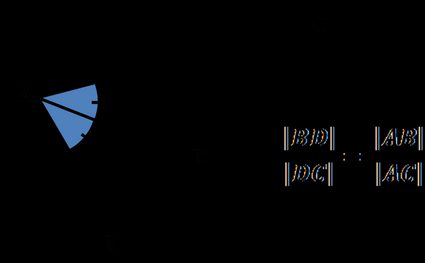
Il teorema della bisettrice dell'angolo afferma che:

La bisettrice dell'angolo di un triangolo divide il lato opposto in due segmenti che sono proporzionali agli altri due lati del triangolo.

O, in altre parole:

Il rapporto tra la lunghezza di $\overline{BD}$ e la lunghezza di $\overline{DC}$ è uguale al rapporto tra la lunghezza del lato $\overline{AB}$ e la lunghezza del lato $\overline{AC}$:

Ok, allora mettiamo in pratica quello che abbiamo appena letto. Supponiamo di voler trovare gli angoli mancanti del nostro triangolo. Come si fa?

1. Scopri quali formule devi usare. Nel nostro esempio abbiamo due lati e un angolo. Scegli l'opzione angolo e 2 lati;
2. Digita i valori indicati. Ad esempio, sappiamo che $a = 9\ \mathrm{cm}$, $b = 14\ \mathrm{cm}$, e $\alpha = 30\degree$. Se vuoi calcolarlo manualmente, usa la legge dei seni:

Quindi:

• Dal teorema sulla somma degli angoli in un triangolo, calcoliamo che $\gamma = 180\degree- \alpha - \beta = 180\degree- 30\degree - 51,\!06\degree= 98,\!94\degree$;

3. Il calcolatore per l'angolo del triangolo trova gli angoli mancanti nel triangolo. Sono uguali a quelli calcolati manualmente:$\beta = 51,\!06\degree$, $\gamma = 98,\!94\degree$; inoltre, lo strumento ha determinato la lunghezza dell'ultimo lato: $c = 17,\!78\ \mathrm{cm}$.

Un ragionamento simile a quello che abbiamo applicato in questo calcolatore compare in altri calcoli di triangoli, ad esempio quelli utilizzati nel calcolatore per triangoli con due angoli e un lato 🇺🇸 e nel calcolatore per triangoli con due lati e un angolo 🇺🇸!