Calcolatore per l'Area del Settore

Con questo calcolatore per l'area del settore, potrai trovare rapidamente l'area del settore di qualsiasi cerchio, ad esempio l'area di un semicerchio o di un quadrante. In questo breve articolo, ci occuperemo di:

• Fornirti una definizione di settore e spiegare cos'è il settore di un cerchio;

• Mostrarti la formula dell'area del settore e spiegare come ricavare l'equazione senza troppa fatica; e

• Svelarti alcuni esempi reali in cui il calcolatore per l'area del settore può essere utile.

Iniziamo con la definizione di settore — cos'è un settore in geometria?

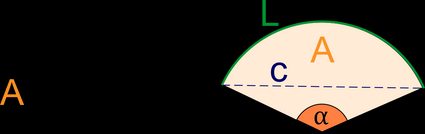
Un settore è una figura geometrica delimitata da due raggi e dall'arco incluso di un cerchio.

I settori di una circonferenza sono più comunemente visualizzati nei grafici a torta, dove una circonferenza viene divisa in diversi settori per mostrare il peso di ogni segmento. Le immagini qui sotto mostrano alcuni esempi di settori di cerchio — non è detto che assomiglino a una fetta di torta, ma a volte assomigliano al resto della torta dopo averne preso una fetta:

Molto raramente si sente parlare del settore di un'ellisse, ma le formule sono molto, molto più difficili da usare rispetto alle equazioni dell'area del settore del cerchio.

La formula per l'area del settore è semplice — moltiplica l'angolo centrale per il raggio al quadrato e dividilo per 2:

• Area del settore = r² × α / 2

Ma da dove deriva? Puoi trovarla utilizzando le proporzioni. Tutto ciò che devi ricordare è la formula dell'area del cerchio (e scommettiamo che la conosci!):

1. L'area di un cerchio si calcola come A = πr². Questo è un ottimo punto di partenza;

2. L'angolo completo è 2π in radianti o 360° in gradi, quest'ultima è l'unità di misura angolare più comune;

3. Quindi, vogliamo calcolare l'area di una parte di un cerchio, espressa dall'angolo centrale;

   • Per angoli di 2π (cerchio completo), l'area è uguale a πr²:

     2π → πr²

   • Quindi, qual è l'area del settore di un cerchio:

     α → Area del settore; e

4. Dalla proporzione, possiamo facilmente trovare la formula finale dell'area del settore:

   Area del settore = α × πr² / 2π = α × r² / 2

Lo stesso metodo può essere utilizzato per trovare la lunghezza dell'arco — basta ricordare la formula della circonferenza di un cerchio. Per saperne di più, leggi il nostro calcolatore della circonferenza e calcolatore per la lunghezza dell'arco.

Trovare l'area di un semicerchio o di un quadrante dovrebbe essere un gioco da ragazzi. Basta pensare a quale parte di cerchio sono!

1. Area del semicerchio: πr² / 2

• Sapendo che è la metà del cerchio, dividi l'area per due:

  Area del semicerchio = area del cerchio / 2 = πr² / 2;

• Naturalmente, otterrai lo stesso risultato utilizzando la formula dell'area del settore. Ricorda solo che l'angolo retto è π (180°):

  Area del semicerchio = α × r² / 2 = πr² / 2

2. Area del quadrante: πr² / 4.

• Poiché un quadrante è un quarto di cerchio, possiamo scrivere la formula come:

  Area del quadrante = area del cerchio / 4 = πr² / 4; e

• L'angolo centrale del quadrante è un angolo retto (π/2 o 90°), quindi si ottiene rapidamente la stessa equazione:

  Area del quadrante = α × r² / 2 = πr² / 4

Lo sappiamo, lo sappiamo — "Perché dobbiamo impararlo? Non la useremo mai e poi mai". Ebbene, vogliamo dimostrarti che la geometria è sempre intorno a noi:

• Se ti stai chiedendo quanto grande debba essere la torta che dovrai ordinare per la tua fantastica festa di compleanno — tombola! Usa la formula dell'area del settore per stimare le dimensioni di una fetta 🍰 per i tuoi ospiti, in modo che nessuno muoia di fame.

• La stessa cosa vale per la pizza — hai notato che ogni fetta è un settore di un cerchio 🍕? Ad esempio, se non sei un grande fan della crosta, puoi calcolare per quale dimensione della pizza ti conviene di più.

• C'è qualche appassionato di cucito qui? 👗 I calcoli per l'area del settore possono essere utili per preparare una gonna a cerchio (dato che non sempre si tratta di un cerchio completo ma, come sai, di un settore di un cerchio).

Oltre a questi semplici esempi di vita reale, la formula dell'area del settore può essere utile in geometria, ad esempio per trovare la superficie di un cono.