Calcolatore per Cerchi

Questo calcolatore per cerchi ti aiuterà a determinare la circonferenza, il diametro, l'area e il raggio di qualsiasi cerchio.

Nell'articolo che segue troverai tutte le formule del cerchio di cui avrai bisogno per calcolare uno di questi valori. Continua a leggere se stai cercando la definizione di cerchio, se vuoi capire come si trova il baricentro o la circonferenza di un cerchio, oppure se vuoi sapere che cos'è il pi greco.

Inoltre, di seguito troverai informazioni sulla circonferenza goniometrica e sulle proprietà di un cerchio, oltre ad alcune curiosità su questa forma: se vuoi sapere qual è il paese più rotondo del mondo, continua a scorrere!

Utilizziamo la seguente notazione:

• c — Circonferenza;
• d — Diametro;
• A —Area; e
• r — Raggio del cerchio.

Preferisci guardare piuttosto che leggere? Impara tutto quello che ti serve in 90 secondi con questo video che abbiamo realizzato per te:

Un cerchio è una curva piana chiusa costituita da un insieme di tutti i punti che si trovano a una determinata distanza da un punto: il centro. In alternativa, puoi definire il cerchio come l'insieme dei punti che si trovano alla stessa distanza da un punto fisso. Il nome cerchio deriva dal greco e significa anello.

Nella lingua inglese, "circle" significa solo un confine circolare, non l'area all'interno della forma. L'intera figura è chiamata "disc". Invece in italiano, un cerchio è l'intera superficie e il confine si chiama semplicemente circonferenza. Il cerchio può essere chiuso se contiene l'arco della circonferenza di 360º che lo delimita, e aperto se la circonferenza è inferiore a 360º.

La terminologia del cerchio consiste nelle definizioni di:

• Circonferenza: la distanza intorno al cerchio;
• Raggio: un segmento che unisce il centro del cerchio con qualsiasi punto della circonferenza;
• Diametro: un segmento i cui estremi si trovano sulla circonferenza e che passa per il centro; e
• Corda: un segmento i cui estremi appartengono alla circonferenza.

Esistono molti altri termini associati al cerchio, come l'arco, la secante o la tangente, ma per le nostre spiegazioni di base è necessario comprendere solo quelli descritti sopra.

Il cerchio è una forma semplice e particolare con molte proprietà insolite:

• Ha la più grande area per una data lunghezza di perimetro;
• È altamente simmetrico: la simmetria per riflessione si verifica per ogni linea che passa per il centro, la simmetria rotazionale intorno al centro per ogni angolo; e
• Può essere costruito attraverso tre punti qualsiasi del piano (non tutti sulla stessa linea). Un cerchio di questo tipo è un cerchio unico.

Inoltre, tutti i cerchi sono simili e i cerchi unici in ogni triangolo possono essere inscritti e circoscritti. Un cerchio ha decine di altre interessanti proprietà che scoprirai man mano leggendo questo articolo.

Le equazioni più popolari associate al cerchio sono:

1. Area del cerchio

   a = πr²;

2. Circonferenza del cerchio

   c = 2πr; e

3. Diametro del cerchio

   d = 2r.

Dalle equazioni di cui sopra puoi ricavare molte altre formule del cerchio, che troverai nei paragrafi dedicati qui di seguito.

Se stai cercando la formula del cerchio vera e propria, dai un'occhiata a questo calcolatore per l'equazione del cerchio 🇺🇸.

La circonferenza goniometrica è un cerchio con raggio uno. Di solito il suo centro è posizionato nell'origine (0, 0) del sistema di coordinate cartesiane.

Scegliamo un punto qualsiasi (x, y) sulla circonferenza goniometrica. Allora |x| e |y| sono le lunghezze dei cateti del triangolo rettangolo, con il raggio del nostro cerchio che è l'ipotenusa di lunghezza 1. Utilizzando il teorema di Pitagora, possiamo scoprire che:

x² + y² = 1

Poiché x² = (-x)², l'equazione di cui sopra funziona per ogni quadrante, non solo per il primo.

Inoltre, possiamo definire i cateti del triangolo rettangolo in termini di seno e coseno:

cos(α) = x / 1 = x

sin(α) = y / 1 = y

Quindi:

sin²(α) + cos²(α) = 1

Questa equazione è nota come identità trigonometrica pitagorica. Per trasformare le tensioni, puoi applicarla al cerchio di Mohr 🇺🇸.

c è la circonferenza del cerchio, ovvero la lunghezza totale della linea tracciata con il compasso. Puoi calcolarla nei seguenti modi:

1. Se conosci il raggio o il diametro del cerchio:

   c = 2πr = πd; e

2. Se il raggio e il diametro sono sconosciuti, allora:

   c = 2√(πa).

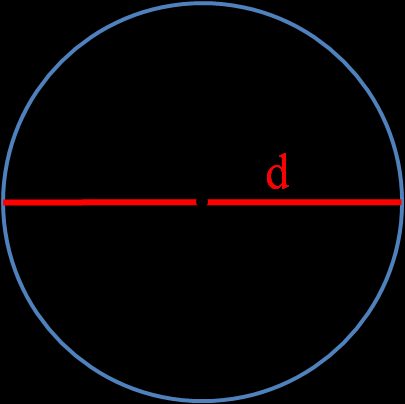
d è il diametro di un cerchio, ovvero la lunghezza di una linea che passa per il punto centrale e unisce due punti del cerchio. Puoi determinarlo con queste equazioni:

1. Se conosci il raggio del cerchio:

   d = 2r;

2. Se il raggio e l'area sono sconosciuti:

   d = c / π; e

3. Se il raggio e la circonferenza sono sconosciuti:

   d = 2√(a / π).

A indica l'area del cerchio. È l'unico valore espresso in unità quadrate (ad esempio, cm²). Puoi calcolarlo come segue:

1. Se conosci il raggio o il diametro del cerchio, la formula dell'area del cerchio è:

   a = πr² = π × (d / 2)²; e

2. Se il raggio e il diametro non sono noti, puoi calcolare l'area in base alla circonferenza:

   a = c² / 4π.

Se ti interessa il calcolo di alcune frazioni di cerchio, controlla:

• Il nostro calcolatore per l'area del semicerchio per trovare l'area di un mezzo cerchio;
• Calcolatore per l'area del settore per verificare l'area di un trancio di pizza; oppure
• Calcolatore per l'area del segmento 🇺🇸, utile per calcolare l'area della sezione trasversale di un tubo parzialmente riempito.

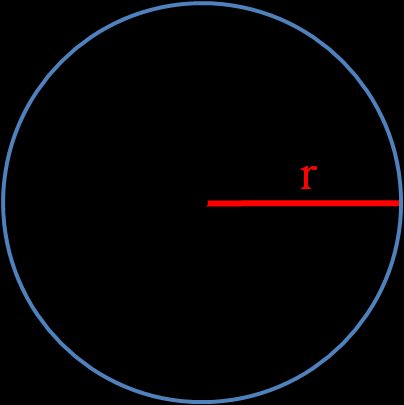
r, o raggio del cerchio, è la lunghezza della linea che unisce il punto centrale con qualsiasi punto del cerchio. Puoi trovarlo con le seguenti formule:

1. Se conosci il diametro del cerchio:

   r = d / 2;

2. Se il diametro e l'area sono sconosciuti:

   r = c / 2π; e

3. Se il diametro e la circonferenza sono sconosciuti:

   r = √(a / π).

Ci sono molti modi per trovare l'origine di un cerchio. Qui ti mostreremo due metodi costruttivi:

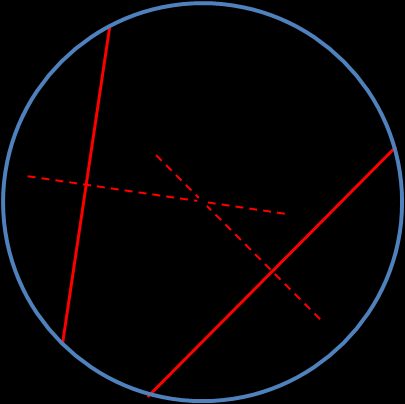
Il primo metodo è una tecnica semplice per trovare l'origine di un cerchio utilizzando un compasso e una riga:

1. Utilizzando un righello o una riga, disegna due corde qualsiasi;
2. Disegna le bisettrici perpendicolari di una delle corde. Usa un compasso per disegnare due cerchi sovrapposti (i loro centri sono gli estremi delle corde, con lo stesso raggio). I cerchi si intersecheranno in due punti: traccia una linea che li attraversa utilizzando una riga;
3. Ripeti la procedura del disegno della bisettrice per la seconda corda; e
4. Le due bisettrici si incroceranno in un punto; questa è l'origine di un cerchio.

Se vuoi, puoi disegnare la terza corda e la sua bisettrice per aumentare e verificare la precisione della determinazione dell'origine di un cerchio.

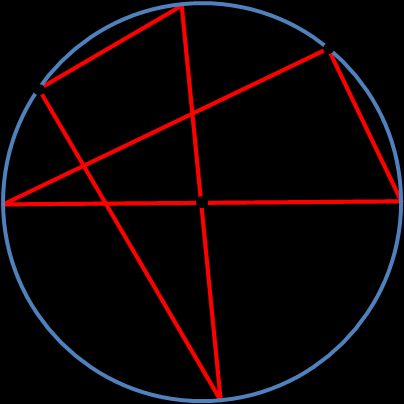
Il secondo metodo è solo una stima approssimativa del centro di un cerchio, ma se non hai bisogno di una grande precisione, puoi usare questa tecnica:

1. Scegli un punto del cerchio;

2. Prendi un oggetto che abbia un angolo di 90 gradi e bordi dritti. Può essere uno strumento di misura per triangoli, ma anche qualsiasi cosa tu abbia a portata di mano, ad esempio un libro, un cartone o un foglio di carta. Posiziona il triangolo in modo che l'angolo retto tocchi il punto scelto;

3. Disegna due linee perpendicolari attraverso il cerchio. Segna i punti in cui si intersecano con il cerchio;

4. Disegna una linea retta che attraversi i punti. Questo è il diametro del cerchio;

5. Puoi trovare il centro di un cerchio tramite:

   • la bisettrice del diametro (come nel primo metodo); oppure
   • semplicemente ripetendo la procedura — scegliendo un altro punto del cerchio, tracciando le linee perpendicolari e creando un altro diametro. L'intersezione di due diametri ci mostrerà il centro del cerchio.

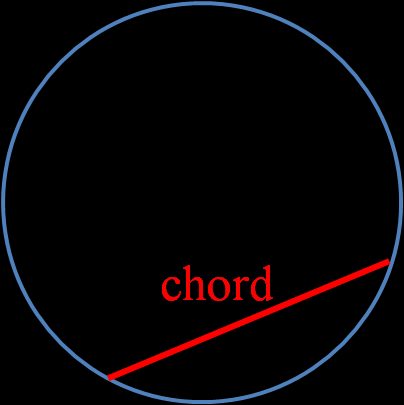
Una corda è un segmento che unisce due punti di una qualsiasi curva. Questa curva può essere un cerchio ma anche, ad esempio, un'ellisse. Se una corda di un cerchio passa per il centro del cerchio, si chiama diametro ed è la corda più lunga possibile.

La corda di un cerchio era molto utilizzata nell'antica trigonometria. Anche se l'abbiamo sostituita con le funzioni trigonometriche, in particolare il seno, è sempre utile sapere come si calcola la sua lunghezza su una circonferenza goniometrica:

Corda(α) = √[(1 - cos(α))² + sin²(α)] = √[2 - 2cos(α)] = 2sin(α/2),

dove α è un angolo centrale, misurato in senso positivo, che deve trovarsi nell'intervallo 0 < α ≤ π.

Possiamo anche ricavare la lunghezza della corda di qualsiasi dimensione del cerchio moltiplicando la corda della circonferenza goniometrica per il raggio del cerchio, r, come mostrato nell'equazione qui sotto:

Corda(α) = r × 2sin(α/2)

I cerchi concentrici sono cerchi con un centro comune. L'oggetto a forma di anello, la regione delimitata da due cerchi concentrici di raggio diverso, è chiamato corona circolare.

Quali sono gli esempi reali di cerchi concentrici?

• Il bersaglio nel tiro con l'arco o il bersaglio di una freccetta;
• Le increspature circolari sull'acqua;
• Gli anelli di crescita degli alberi (circa); e
• I solchi di un disco in vinile o di un CD.

Il pi greco è la costante matematica più conosciuta. È il rapporto tra la circonferenza di un cerchio e il suo diametro:

π = circonferenza / diametro

Indipendentemente dalle dimensioni del cerchio, il rapporto c/d è costante. Di solito, la costante pi greco è approssimata a un paio di cifre, ad esempio quattro o sei. Le prime 40 cifre decimali sono:

π ≈ 3,14159 26535 89793 23846 26433 83279 50288 41971...

Il π è un numero irrazionale, il che significa che nessun numero finito di cifre può rappresentare esattamente π (e non si ripete mai). Il Pi greco è stato calcolato con oltre ventiduemila miliardi di cifre oltre la virgola e questo numero continua ad aumentare con lo sviluppo della tecnologia informatica.

Esistono gare in cui i concorrenti cercano di memorizzare il maggior numero possibile di cifre del pi greco. Il record mondiale certificato dal Guinness World Records è di 70.000 cifre, mentre un ingegnere giapponese in pensione detiene un record non ufficiale di oltre 100.000 cifre.

Lo sapevi che...

• Esiste uno stile di scrittura chiamato pilish, degli stratagemmi per ricordare le cifre di un numero. La lunghezza delle parole consecutive corrisponde alle cifre del pi greco. Ad esempio:

  • Può l'odio d'Iside imprecare su sfinge rotta? – 314159265 in pilish se nove cifre da ricordare sono sufficienti; e

  • Ave o Roma o Madre gagliarda di latine virtù che tanto luminoso splendore prodiga spargesti con la tua saggezza. – per diciannove cifre.

  Si tratta di un metodo eccellente per memorizzare le cifre del pi greco, poiché il cervello è molto più abile nel ricordare le parole che le grandi stringhe di numeri. Forse potresti esercitare la tua mente e inventare la tua storia del pi greco?

• Sono stati pubblicati diversi libri sulla costante pi greco. Tra questi ci sono, ovviamente, saggi matematici standard, ma non solo: anche libri completi sono scritti in pilish! Quello intitolato "Not A Wake: A Dream Embodying π's Digits Fully for 10000 Decimals" di Mike Keith detiene il record del più lungo testo in pilish con 10 000 cifre.

• Esiste il giorno del pi greco celebrato da molti appassionati di π. È il 14 marzo, come suggerisce la data americana (3/14). Qualche anno fa, nel 2015, c'è stato un giorno del Pi greco "speciale", in quanto le due cifre successive sono apparse nella data (3/14/15). E l'orario - 9:26:53 - ha aggiunto ancora più cifre! Come puoi festeggiare questa speciale giornata geek? Vestiti come Albert Einstein (che compie gli anni il giorno del pi greco) e mangia tutto il giorno delle prelibatezze circolari: dalle ovvie torte, ai pancake, alle pizze quasi perfettamente rotonde.

• Anche se imparare il π a centinaia o migliaia di cifre può essere divertente (?), è stato determinato che solo 38 decimali sono sufficienti per misurare la circonferenza dell'Universo osservabile, con la precisione della larghezza di un atomo di idrogeno. Guarda il video sul π e le dimensioni dell'Universo del matematico James Grime sul canale Youtube Numberphile.

Nell'uso quotidiano, la quadratura del cerchio è una metafora per indicare la lotta contro compiti difficili o addirittura impossibili. Ma cosa significa da un punto di vista matematico?

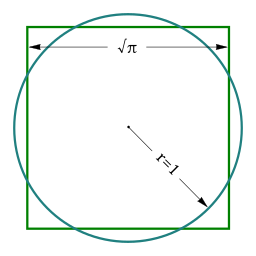
È stato un problema per i matematici fin dall'antichità. Si tratta del compito di disegnare un quadrato di area uguale a quella di un cerchio ma utilizzando solo una riga e un compasso. Il problema si è rivelato impossibile da risolvere nel 1882 quando il matematico Lindemann ha dimostrato che π è un numero trascendentale; pertanto, π e √π non possono essere costruiti. Tuttavia, se rimuoviamo il vincolo di riga e compasso, il problema è facile ed è già stato risolto e descritto molte volte.

Puoi incontrare la combinazione di parole quadrato e cerchio nella vita di tutti i giorni: i ring di pugilato e wrestling sono conosciuti come cerchi quadrati. Il nome deriva dalla forma simile a un anello.

Il cerchio è una forma 2D che funge da base per alcune forme geometriche curvilinee 3D.

Un cilindro ha due basi parallele (solitamente circolari). Inoltre, l'unica base di un cono è spesso un cerchio.

Conoscendo la formula dell'area di un cerchio, possiamo calcolare facilmente i volumi di queste forme:

v(cilindro) = πr²h

v(cono) = πr²h/3

Per quanto riguarda la sfera, si tratta di un oggetto geometrico perfettamente rotondo nello spazio 3D che rappresenta la superficie di una palla completamente rotonda. È analoga al cerchio e al disco, ma in tre dimensioni e non in due.

Inoltre, esiste il termine cerchio di una sfera che indica un cerchio che giace su una sfera.

Un grande cerchio è quello il cui piano passa per il centro della sfera; qualsiasi altro cerchio è chiamato piccolo cerchio. Viene utilizzato, ad esempio, in cartografia e geografia: l'equatore è l'unico cerchio massimo della famiglia dei paralleli di latitudine. Tuttavia, tutti i meridiani di longitudine, accoppiati con il meridiano opposto, formano dei cerchi massimi.

Possiamo confrontare i paesi in molti modi: in base alla loro area, alla popolazione o al PIL, ma ti chiedi mai quale sia il paese più tondo del mondo?

Un matematico e blogger, Gonzalo Ciruelos, ha calcolato il parametro della rotondità e ha creato la classifica. Il vincitore della categoria rotondità è la Sierra Leone, mentre il titolo di paese meno rotondo del mondo va alle Isole Marshall.

La Sierra Leone è al 1° posto per la circolarità, ma è anche al 14° posto in un'altra classifica: il paese più rettangolare del mondo! Per confondere ancora di più le idee, il 4° paese più rotondo, la Città del Vaticano, è il 2° paese più rettangolare del mondo e la Polonia, 5° nella classifica della rotondità, è 10° in quella della rettangolarità. Come è possibile essere rettangolari e rotondi allo stesso tempo?!

È tutta una questione di definizione di rettangolarità e rotondità, che potrebbe non essere adeguata per forme complesse o sparse, e i confini delle nazioni di solito lo sono.

Puoi trovare una spiegazione e una discussione migliore dei risultati sul sito web di bigthink.

Se hai ancora dubbi su come si usa il nostro calcolatore dei cerchi, dai un'occhiata a questa illustrazione:

1. Supponiamo di voler calcolare le dimensioni di un cerchio nel grano. Sceglieremo quello ispirato all'identità di Eulero, trovato nel 2010 a Wilton, vicino a Marlborough, nel Regno Unito. L'identità di Eulero è un caso speciale della formula di Eulero (che può essere derivata dalla circonferenza goniometrica nel piano complesso).

2. Digita la dimensione data nel calcolatore dei cerchi. Sappiamo che il cerchio nel grano aveva un diametro di circa 300 piedi. Se hai bisogno di cambiare le unità di misura, clicca sul nome dell'unità e scegli quella che ti serve da un elenco a tendina (piedi nel nostro caso); ed

3. Ecco fatto! Grazie a questo fantastico strumento, hai scoperto tutti i parametri del cerchio in un batter d'occhio! Ora sappiamo che la:

   • La circonferenza del cerchio è pari a 90 metri;
   • Il raggio è pari a 45 metri; e
   • L'area è di 6361,7 metri², ovvero quasi l'area di un campo da calcio! (Per essere più precisi: ~92% dell'area di un campo da calcio)

Sperimenta con il calcolatore per cerchi e prova diversi calcoli! A proposito di cerchi, perché non verificare qual è la circonferenza della ruota della tua bicicletta?